上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.5 Equilibrium Problem

6.5 Equilibrium Problem Equilibrium Definition A system is said to be in equilibrium if it remains stationary under the action of applied forces i=9=0 Dynamic equation M9+Φ，'=2 i=0 Equilibrium equation D,九=

q  q  0 T A Mq q   Q T A  q   Q A system is said to be in equilibrium if it remains stationary under the action of applied forces Equilibrium Definition Dynamic equation Equilibrium equation q  0 6.5 Equilibrium Problem

Equilibrium Condition Solve Φ，2=04 and 1Φ(q)=0 Since they are nonlinear algebraic equations,Newton-Raphson Method can be used for solution,however,the initial value of A is difficult to estimate q=u'v v:Independent coordinates To solve this problem,transformation method is used 0,=②。中]0 Φ1=2 e Φ，九=2， →=（西，0 Equilibrium Condition H'Q=2,H=ΦΦ

Equilibrium Condition Solve T A  q   Q and (q)  0 Since they are nonlinear algebraic equations, Newton-Raphson Method can be used for solution, however, the initial value of  is difficult to estimate To solve this problem, transformation method is used    q   u  v A v T A u T Q Q v u         A u T u Q 1           A v A u A Q Q Q A v A u T H Q  Q H  u  v 1  Equilibrium Condition   v: Independent coordinates T T T q  u v

Example 6.10 X Single pendulum is shown in the figure.The length of the pendulum is 21,and the mass of the pendulum is m.The Coefficient of the rotational spring is ke.The pendulum is applied with gravitational force.Find the equilibrium condition g X1

Example 6.10 x1 y1 C x y f g kq Single pendulum is shown in the figure. The length of the pendulum is 2l, and the mass of the pendulum is m. The Coefficient of the rotational spring is kq . The pendulum is applied with gravitational force. Find the equilibrium condition

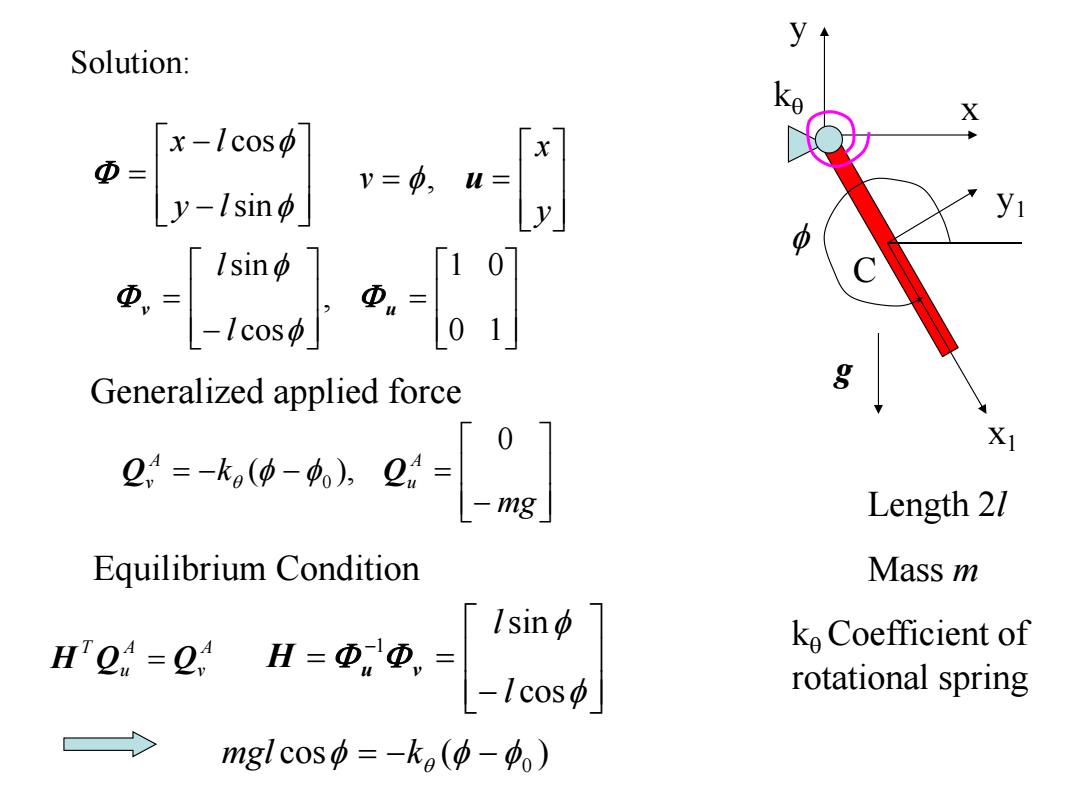
Solution: X x-lcosφ Φ= -1sn v=0,u= y 10 Generalized applied force g e-wse-l Length 21 Equilibrium Condition Mass m [lsinφ I2:-Q:H-losd ko Coefficient of rotational spring mgl cos中=-kg(p-中)

x1 y1 C x y f g Length 2l Mass m kq kqCoefficient of rotational spring           0 1 1 0 , cos sin  v  u f f l l        f f sin cos y l x l        y x v f, u Equilibrium Condition A v A u T H Q  Q Generalized applied force         mg k A u A v 0 ( ), Q q f f 0 Q        f f cos sin 1 l l H  u  v cos ( ) f   q f f 0 mgl k Solution:

Example 6.11 Double pendulum is shown in the figure.The length of each link is 27,and X the mass of each link is m.A horizontal Br force is applied at the tip point of B2 y1 Each pendulum is applied with gravitational force.Find the 中1 equilibrium condition g X 2 p2 F X2

Example 6.11 x1 y1 C1 x y f1 g x2 y2 C2 f2 F P Double pendulum is shown in the figure. The length of each link is 2l, and the mass of each link is m. A horizontal force is applied at the tip point of B2 . Each pendulum is applied with gravitational force. Find the equilibrium condition B2 B1

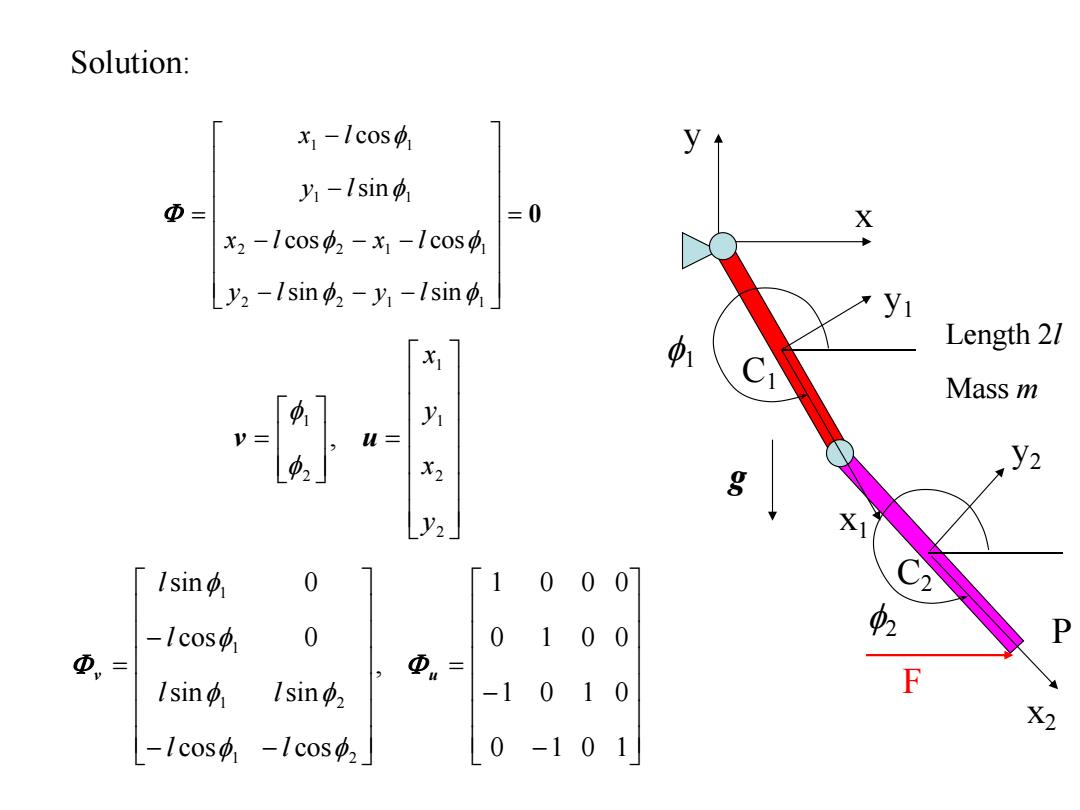
Solution: x-Icos y-Isin Φ= =0 X x2-lcos中2-x1-1cos中1 y2-Isin2-y,-lsin中， yi 1 Length 2/ XI Mass m y v= l 中2」 X2 g y2 X Ising 0 1 00 0 -1c0sφ1 0 0 100 P ①，= Φ.= Ising Isin2 -1 010 F X2 -lcos中，-Icos2 0-101

x1 y1 C1 x y f1 g x2 y2 C2 f2 Length 2l Mass m F P  0                2 2 1 1 2 2 1 1 1 1 1 1 sin sin cos cos sin cos f f f f f f y l y l x l x l y l x l              2 2 1 1 2 1 , y x y x v u f f                   0 1 0 1 1 0 1 0 0 1 0 0 1 0 0 0 , cos cos sin sin cos 0 sin 0 1 2 1 2 1 1  v  u f f f f f f l l l l l l Solution:

Isin 0 「10 00 -Icos 0 010 0 。= Isin Isin2 一1 010 -1cos41-1cosφ2 0-101 lsinφ1 0 -1cos 0 H=DΦ。= 21sin Isin -21cos -Icos

                  0 1 0 1 1 0 1 0 0 1 0 0 1 0 0 0 , cos cos sin sin cos 0 sin 0 1 2 1 2 1 1  v  u f f f f f f l l l l l l            1 2 1 2 1 1 1 2 cos cos 2 sin sin cos 0 sin 0 f f f f f f l l l l l l H  u  v

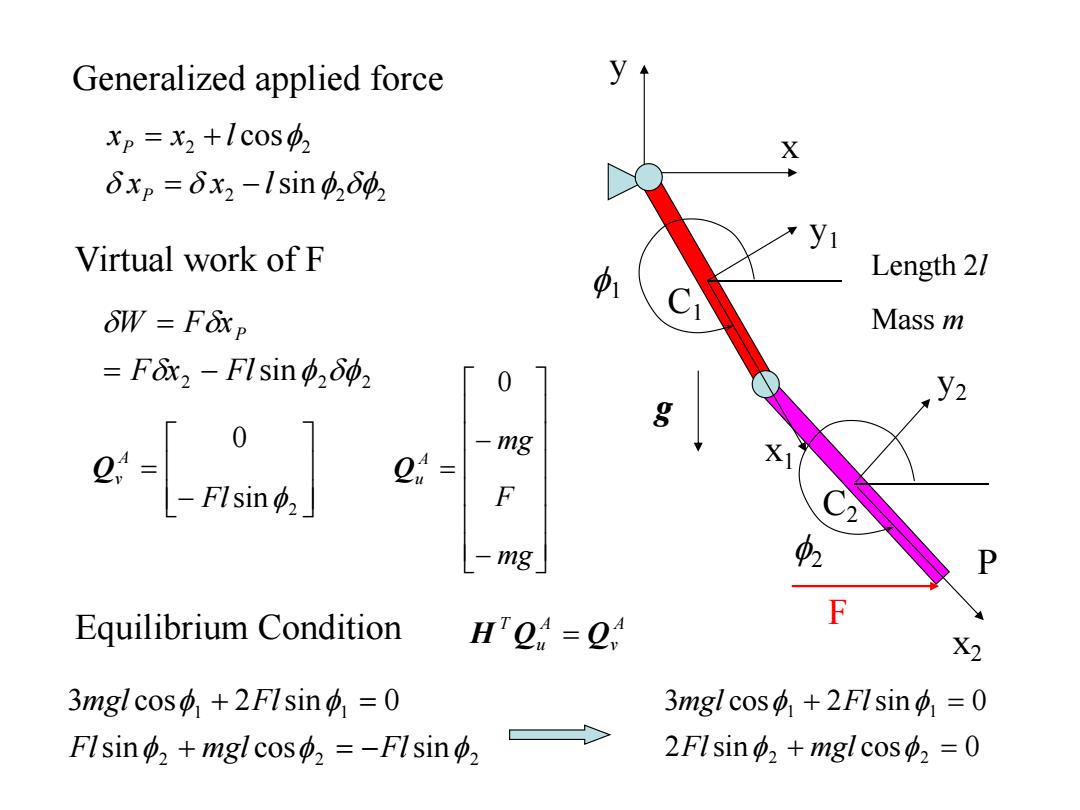
Generalized applied force xp=x2 +lcos X δxp=δx2-Isin2δ冲2 Virtual work of F Length 2/ δW=Fxp Mass m =Fx2-Flsin2δp2 0 g eLa -mg 2= X F -mg 2 Equilibrium Condition F H2=2,4 3mgl coso +2FIsin=0 3mgl coso +2FIsin=0 FIsin2 +mgl cos,=-FIsin2 2FIsin2 mgl cos2=0

Generalized applied force x1 y1 C1 x y f1 g x2 y2 C2 f2 Length 2l Mass m F P 2 2 2 2 2 sin cos   f f f x x l x x l P P     2 2 2  sinf f   F x Fl W F xP         2 sin 0 Fl f A Qv Virtual work of F A v A u T Equilibrium Condition H Q  Q         mg F mg A u 0 Q 2 2 2 1 1 sin cos sin 3 cos 2 sin 0 f f f f f Fl mgl Fl mgl Fl      2 sin cos 0 3 cos 2 sin 0 2 2 1 1     f f f f Fl mgl mgl Fl

Problem Equation Φ，'=Q4 is computationally feasible However A good estimate of the equilibrium position is needed as a starting point for iterative computation The difficulty associated with unstable equilibrium configuration The principle of minimum total potential energy is employed in order to avoid the difficulty

• A good estimate of the equilibrium position is needed as a starting point for iterative computation • The difficulty associated with unstable equilibrium configuration is computationally feasible T A Equation  q   Q However The principle of minimum total potential energy is employed in order to avoid the difficulty Problem

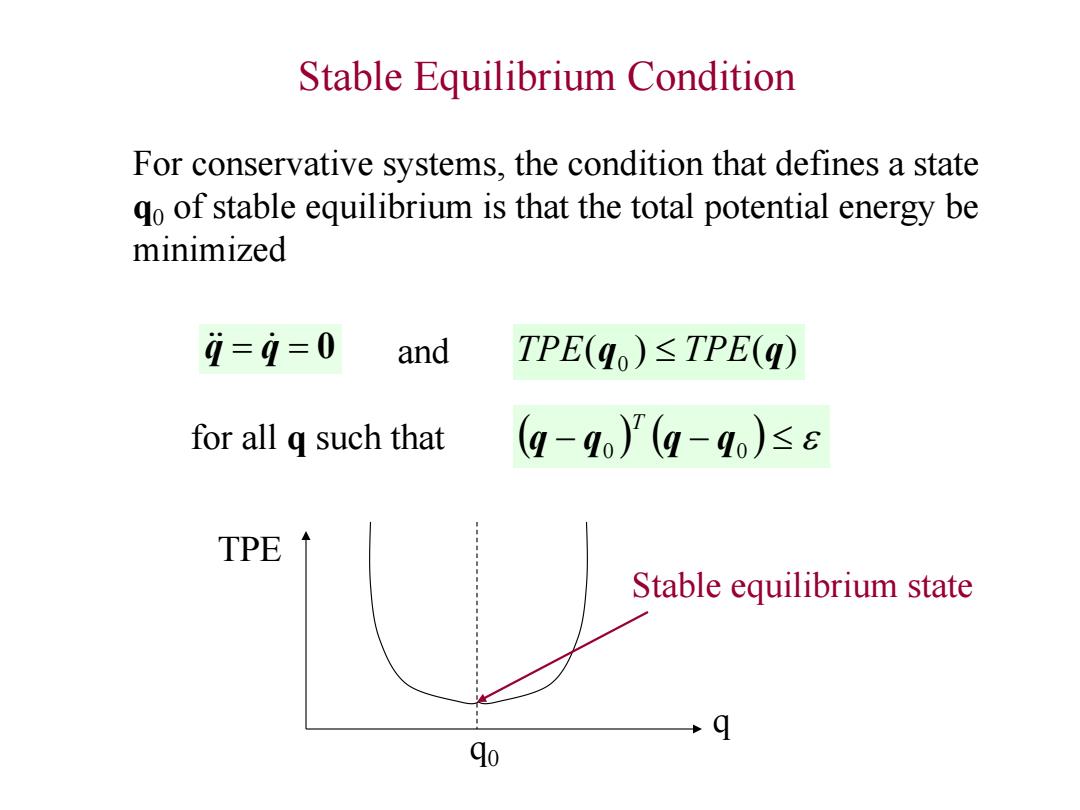
Stable Equilibrium Condition For conservative systems,the condition that defines a state qo of stable equilibrium is that the total potential energy be minimized 4=9=0 and TPE(qO)≤TPE(q) for all q such that (q-qa)'(q-go)≤ε TPE Stable equilibrium state q 90

Stable Equilibrium Condition ( ) ( ) q  q  0 and TPE q0  TPE q for all q such that         q q0 q q0 T For conservative systems, the condition that defines a state q0 of stable equilibrium is that the total potential energy be minimized q TPE q0 Stable equilibrium state