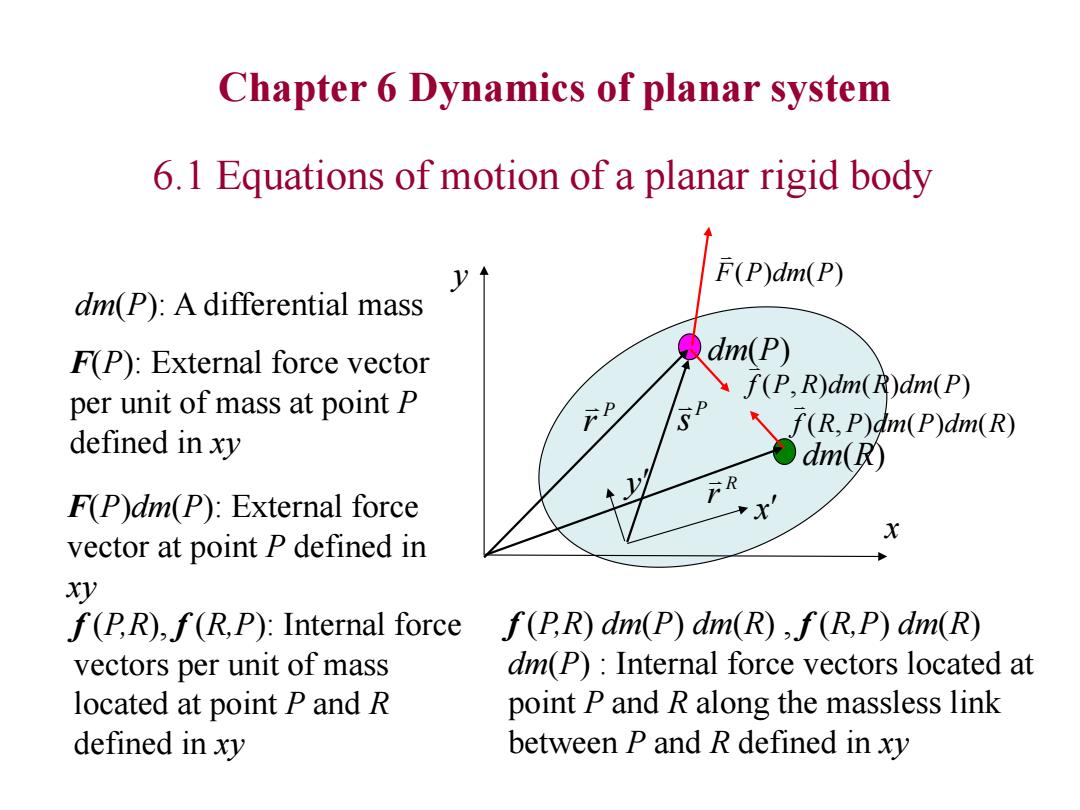
Chapter 6 Dynamics of planar system 6.1 Equations of motion of a planar rigid body F(P)dm(P) dm(P):A differential mass F(P):External force vector dm(P) per unit of mass at point P f(P,R)dm(R)dm(P) defined in xy 价 户R F(P)dm(P):External force vector at point P defined in X XV f(PR),f(R,P):Internal force f(P.R)dm(P)dm(R),f(R,P)dm(R) vectors per unit of mass dm(P):Internal force vectors located at located at point P and R point P and R along the massless link defined in xy between P and R defined in xy
Chapter 6 Dynamics of planar system 6.1 Equations of motion of a planar rigid body x y dm(P) P r P s dm(R) R r x y F(P)dm(P) f (P, R)dm(R)dm(P) f (R, P)dm(P)dm(R) dm(P): A differential mass F(P): External force vector per unit of mass at point P defined in xy F(P)dm(P): External force vector at point P defined in xy f (P,R), f (R,P): Internal force vectors per unit of mass located at point P and R defined in xy f (P,R) dm(P) dm(R) , f (R,P) dm(R) dm(P) : Internal force vectors located at point P and R along the massless link between P and R defined in xy

6.1.1 Variational equations of motion from Newton's Equation Newton's Equations of motion Fdm(P)=F(P)dm(P)+f(P,R)dm(R)dm(P) Let &rP denote an arbitrary virtual displacement of point of p Premultiplying both sides by 8rPT and integrating over the total mass of the body yields m(P)F(P)dm(P)P.Rdim(R)dm(P) F(P)dm(P) dm(P) f(P,R)dm(R)dm(P) 公) XgPa网 户R X
6.1.1 Variational equations of motion from Newton’s Equation x y dm(P) P r P s dm(R) R r x y F(P)dm(P) f (P, R)dm(R)dm(P) f (R, P)dm(P)dm(R) Newton’s Equations of motion dm(P) (P)dm(P) (P, R)dm(R) dm(P) m P r F f Let d rP denote an arbitrary virtual displacement of point of P Premultiplying both sides by d rPT and integrating over the total mass of the body yields m m T P m T P m P T P d r r dm(P) d r F(P)dm(P) d r f (P, R)dm(R)dm(P)

[δrP'Pdm(P)=∫n6rPrF(P)dmP)+∫nnδrP'f(P,R)dim(R)dm(P) Since∫nfnδr'f(P,R)dm(R)adn(P) (P.Rydm(R)dm(P)(P.R)dm(Rydm(P) r"f(P,RYdm(R)dm(P)+r"f(R,P)dm(P)dm(R) Jjδr"f(P,R)dim(R)dm(P)-∫n∫n&rR'fP,R)dimP)dim(R) (r"-rk)f(P.R)dm(R)dm(P) And for rigid body,the distance between P and R remains constant (rP-rR)T(rP-rR)=C 6(rP-rR)7(rP-rR)+(rP-rR)76(rP-rR)=0 8(rP-rR)7(rP-rR)=(rP-rR)76(rP-rR)>5(rP-rR)7(rP-rR)=0 Since f(P,R)acts along the line between P and R,f(P,R)=-c(r-r") r"(P.R)dm(R)dm(P)-(r(r-r)dm(R)dm(P)-0
m m T P m T P m P T P d r r dm(P) d r F(P)dm(P) d r f (P, R)dm(R)dm(P) m m P R T m m T R m m T P m m T R m m T P m m T P m m T P m m T P P R dm R dm P P R dm R dm P P R dm P dm R P R dm R dm P R P dm P dm R P R dm R dm P P R dm R dm P P R dm R dm P ( ) ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) 2 1 ( , ) ( ) ( ) r r f r f r f r f r f r f r f r f d d d d d d d d Since And for rigid body, the distance between P and R remains constant C P R T P R (r r ) (r r ) ( ) ( ) ( ) ( ) 0 P R T P R P R T P R d r r r r r r d r r ( ) ( ) ( ) ( ) P R T P R P R T P R d r r r r r r d r r ( ) ( ) 0 P R T P R d r r r r Since f (P, R) acts along the line between P and R, ( , ) ( ) P R f P R c r r ( ) ( ) ( ) ( ) 0 2 1 ( , ) ( ) ( ) m m P R T P R m m T P d r f P R dm R dm P cd r r r r dm R dm P

Variational equations of motion [n6rP'Ffdm(P)=∫δrPrF(P)dim(P) Since rP=r+As'P 6rP=δr+6As'P and M-mg-ga】w8 P=护+BsP-2AsP δrP=6r+Bs'P6 One obtains δr'dm(P)+[6r'(B-D2A)+δ动rB]s'fdm(P) s"B"(BA)s"dm(P)=rF(P)dm(P)s"B'F(P)dm(P)
m T P m P T P d r r dm(P) d r F(P)dm(P) Variational equations of motion Since P P r r As P P d r d r dAs A dB d d d cos sin sin cos sin cos cos sin and P P P r r Bs As 2 One obtains m T T P m T m T P T P m T T P m T dm P P dm P P dm P dm P dm P ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( ) ] ( ) 2 2 s B B A s r F s B F r r r B A r B s d d d d d d d d d P P r r Bs

6.1.2 Variational equations of motion with Centroidal Coordinates The general variational form of the equations of planar motion 6r"dm(P)+[r"(B-2A)+8r"B]s"dm(P) +s"B"(BA)s"dm(P)=5r"[F(P)dm(P)s"B'F(P)dm(P) This form of the equations can be substantially simplified if special features of the body-fixed frame are exploited The first integral on the left is simplify the total mass of the body m=dm(P) Regardless of the location of the body-fixed frame
6.1.2 Variational equations of motion with Centroidal Coordinates m T T P m T m T P T P m T T P m T dm P P dm P P dm P dm P dm P ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( ) ] ( ) 2 2 s B B A s r F s B F r r r B A r B s d d d d d d The general variational form of the equations of planar motion This form of the equations can be substantially simplified if special features of the body-fixed frame are exploited m m dm(P) The first integral on the left is simplify the total mass of the body Regardless of the location of the body-fixed frame

If the origin of the body-fixed frame is located at the center of mass or centroid of the body,then,by definition of the centroid ∫ns'dim(P)=ms'c=0 The second integral on the left vanishes Direct matrix multiplications verify that BB=I Since B=RA One obtains BA=R 4B-R-[90 s'PTBT As'P=0 [sB"(B-A)s"dm(P) sB'Bsdm(P)sB"As"dm(P)=ss"dm(p)= J'is the polar moment of inertia of the body with respect to the origin of the body-fixed frame
B B I T If the origin of the body-fixed frame is located at the center of mass or centroid of the body, then, by definition of the centroid The second integral on the left vanishes 0 C m P s dm(P) ms Direct matrix multiplications verify that Since B RA BA R T One obtains 1 0 0 1 T T A B R dm P dm P dm P J dm P m P T P m T P T P m T P T P m T P T P ( ) ( ) ( ) ( ) ( ) 2 2 s B Bs s B As s s s B B A s 0 T P T P s B As is the polar moment of inertia of the body with respect to the origin of the body-fixed frame J

One obtains the variational equations of motion δr'(mr-F)+0'-n)=0 F=∫nF(P)dm(P) n=[s'P'B'F(P)dm(P)
m T TP m n P dm P P dm P ( ) ( ) ( ) ( ) s B F F F m n 0 T d d r r F J One obtains the variational equations of motion