
二参数温度模型的参数识别与实验验证 目录 1.1DQ200改进的温度模型的推导. 1 1.2DQ200关于模型的假设 .2 1.3DQ200温度模型参数辨识 6 1.3.1参数辨识方法 6 1.3.2在MATLAB中实现最小二乘法参数辨识 1 1.3.3模型1参数辨识结果. 1.3.4模型1的实验验证结果 8 1.3.5模型2参数辨识结果… 10 1.3.6模型2的实验验证结果.… 10 1.3.7原有的二参数温度模型的参数识别 .12 1.3.8原有的二参数温度模型的实验验证 .13 1.4DCT250改进的温度模型参数辨识… .18 1.4.1模型3参数识别结果. 23 1.4.2模型3试验验证结果 23 1.4.3模型4参数识别结果 26 1.4.4模型4实验验证结果 26 1.4.5相同环境温度下滑摩功率与k,k2的关系 29 1.4.6环境温度为26℃参数识别结果… 30 1.4.7环境温度为26℃实验验证结果.… .31 1.4.8环境温度为28℃参数识别结果. 32 1.4.9环境温度为28℃实验验证结果 32 1.4.10四参数温度模型假设… .33 1.4.11四参数温度模型参数识别. .34 1.4.12四参数温度模型实验验证. .34 1.1DQ200改进的温度模型的推导 原有的二参数温度模型: 7- -=kF0o0-k(T0-T.) \MERGEFORMAT (1) △f 上式中为离合器压盘半径,处的温度,F为摩擦界面的正压力,T。为环境空气温度,⊙ 为摩擦界面的转速差。k,为温升系数,k2为散热系数。 其中温升系数k1,和散热系数k,的值均为未知量,若利用该温度模型预测离合器温度 必须先辨识k,k,的值。利用实验数据对不同的工况下的k,k,值进行辨识,发现k1,k2 的值与滑摩功率的大小直接相关。可假设k1,k2与P为线性相关或者指数相关,并分别用
二参数温度模型的参数识别与实验验证 目录 1.1DQ200 改进的温度模型的推导........................................................................................... 1 1.2DQ200 关于模型的假设....................................................................................................... 2 1.3DQ200 温度模型参数辨识................................................................................................... 6 1.3.1 参数辨识方法........................................................................................................... 6 1.3.2 在 MATLAB 中实现最小二乘法参数辨识............................................................... 7 1.3.3 模型 1 参数辨识结果............................................................................................... 8 1.3.4 模型 1 的实验验证结果........................................................................................... 8 1.3.5 模型 2 参数辨识结果............................................................................................. 10 1.3.6 模型 2 的实验验证结果........................................................................................ 10 1.3.7 原有的二参数温度模型的参数识别..................................................................... 12 1.3.8 原有的二参数温度模型的实验验证..................................................................... 13 1.4DCT250 改进的温度模型参数辨识....................................................................................18 1.4.1 模型 3 参数识别结果............................................................................................. 23 1.4.2 模型 3 试验验证结果............................................................................................. 23 1.4.3 模型 4 参数识别结果............................................................................................. 26 1.4.4 模型 4 实验验证结果............................................................................................. 26 1.4.5 相同环境温度下滑摩功率与 1 2 k , k 的关系........................................................... 29 1.4.6 环境温度为 26℃参数识别结果............................................................................ 30 1.4.7 环境温度为 26℃实验验证结果............................................................................ 31 1.4.8 环境温度为 28℃参数识别结果............................................................................ 32 1.4.9 环境温度为 28℃实验验证结果............................................................................ 32 1.4.10 四参数温度模型假设........................................................................................... 33 1.4.11 四参数温度模型参数识别................................................................................... 34 1.4.12 四参数温度模型实验验证................................................................................... 34 1.1DQ200 改进的温度模型的推导 原有的二参数温度模型: i+1 i 1 2 n n i i i n T T k F k T T t \* MERGEFORMAT (1) 上式中 i Tn 为离合器压盘半径 r 处的温度,F 为摩擦界面的正压力,T 为环境空气温度, 为摩擦界面的转速差。 k 1 为温升系数, k 2 为散热系数。 其中温升系数 k 1 ,和散热系数 k 2 的值均为未知量,若利用该温度模型预测离合器温度 必须先辨识 k 1 ,k 2 的值。利用实验数据对不同的工况下的 k 1 ,k 2 值进行辨识,发现 k 1 ,k 2 的值与滑摩功率的大小直接相关。可假设 k 1 ,k 2 与 P 为线性相关或者指数相关,并分别用
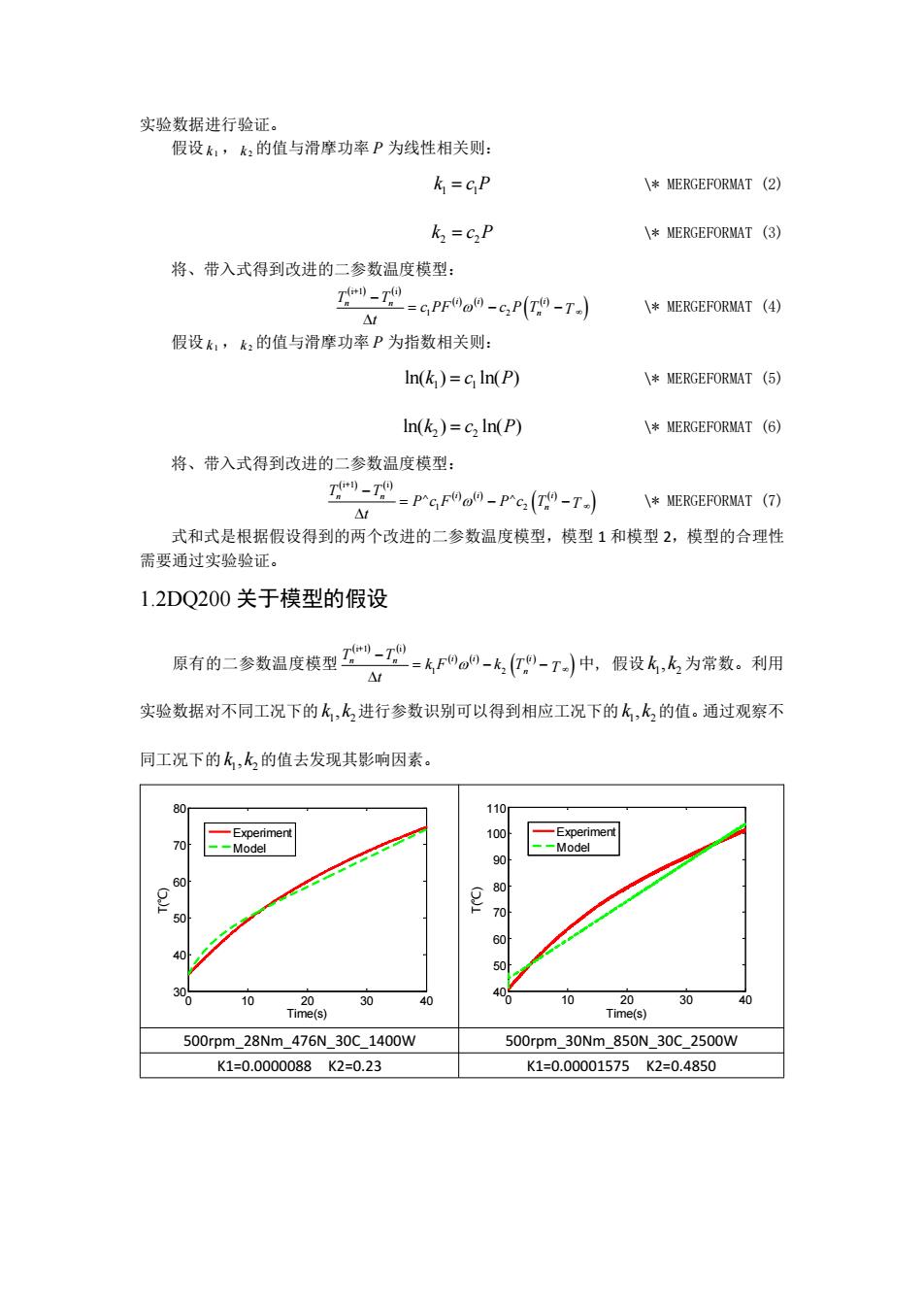
实验数据进行验证。 假设k,k2的值与滑摩功率P为线性相关则: k=cP \MERGEFORMAT (2) k,=C,P \MERGEFORMAT (3) 将、带入式得到改进的二参数温度模型: -70 =cPF0o0-c,P(T9-T) \MERGEFORMAT (4) △t 假设k1,k2的值与滑摩功率P为指数相关则: In(k )=c In(P) \MERGEFORMAT (5) In(k)=c2 In(P) \MERGEFORMAT (6) 将、带入式得到改进的二参数温度模型: 1-TPcFO00-P"c:(T-T) \MERGEFORMAT (7) △t 式和式是根据假设得到的两个改进的二参数温度模型,模型1和模型2,模型的合理性 需要通过实验验证。 1.2DQ200关于模型的假设 原有的二参数温度模型:空-ko-.,的-T中,假设么,k为常数。利用 △ 实验数据对不同工况下的k,k进行参数识别可以得到相应工况下的k,k,的值。通过观察不 同工况下的k,k的值去发现其影响因素。 % 110 -Experiment 100 -Experiment 70 --Model --Model 90 60 g 80 % % SO 0 10 20 30 40 00 10 20 30 40 Time(s) Time(s) 500rpm_28Nm_476N_30C1400W 500rpm_30Nm_850N_30C_2500W K1=0.0000088K2=0.23 K1=0.00001575K2=0.4850
实验数据进行验证。 假设 k 1 ,k 2 的值与滑摩功率 P 为线性相关则: 1 1 k c P \* MERGEFORMAT (2) 2 2 k c P \* MERGEFORMAT (3) 将、带入式得到改进的二参数温度模型: i+1 i 1 2 n n i i i n T T c PF c P T T t \* MERGEFORMAT (4) 假设 k 1 ,k 2 的值与滑摩功率 P 为指数相关则: 1 1 ln(k ) c ln(P) \* MERGEFORMAT (5) 2 2 ln(k ) c ln(P) \* MERGEFORMAT (6) 将、带入式得到改进的二参数温度模型: i+1 i 1 2 n n i i i n T T P c F P c T T t \* MERGEFORMAT (7) 式和式是根据假设得到的两个改进的二参数温度模型,模型 1 和模型 2,模型的合理性 需要通过实验验证。 1.2DQ200 关于模型的假设 原有的二参数温度模型 i+1 i 1 2 n n i i i n T T k F k T T t 中, 假设 1 2 k ,k 为常数。利用 实验数据对不同工况下的 1 2 k ,k 进行参数识别可以得到相应工况下的 1 2 k ,k 的值。通过观察不 同工况下的 1 2 k ,k 的值去发现其影响因素。 0 10 20 30 40 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 0 10 20 30 40 40 50 60 70 80 90 100 110 Time(s) T(℃) Experiment Model 500rpm_28Nm_476N_30C_1400W 500rpm_30Nm_850N_30C_2500W K1=0.0000088 K2=0.23 K1=0.00001575 K2=0.4850
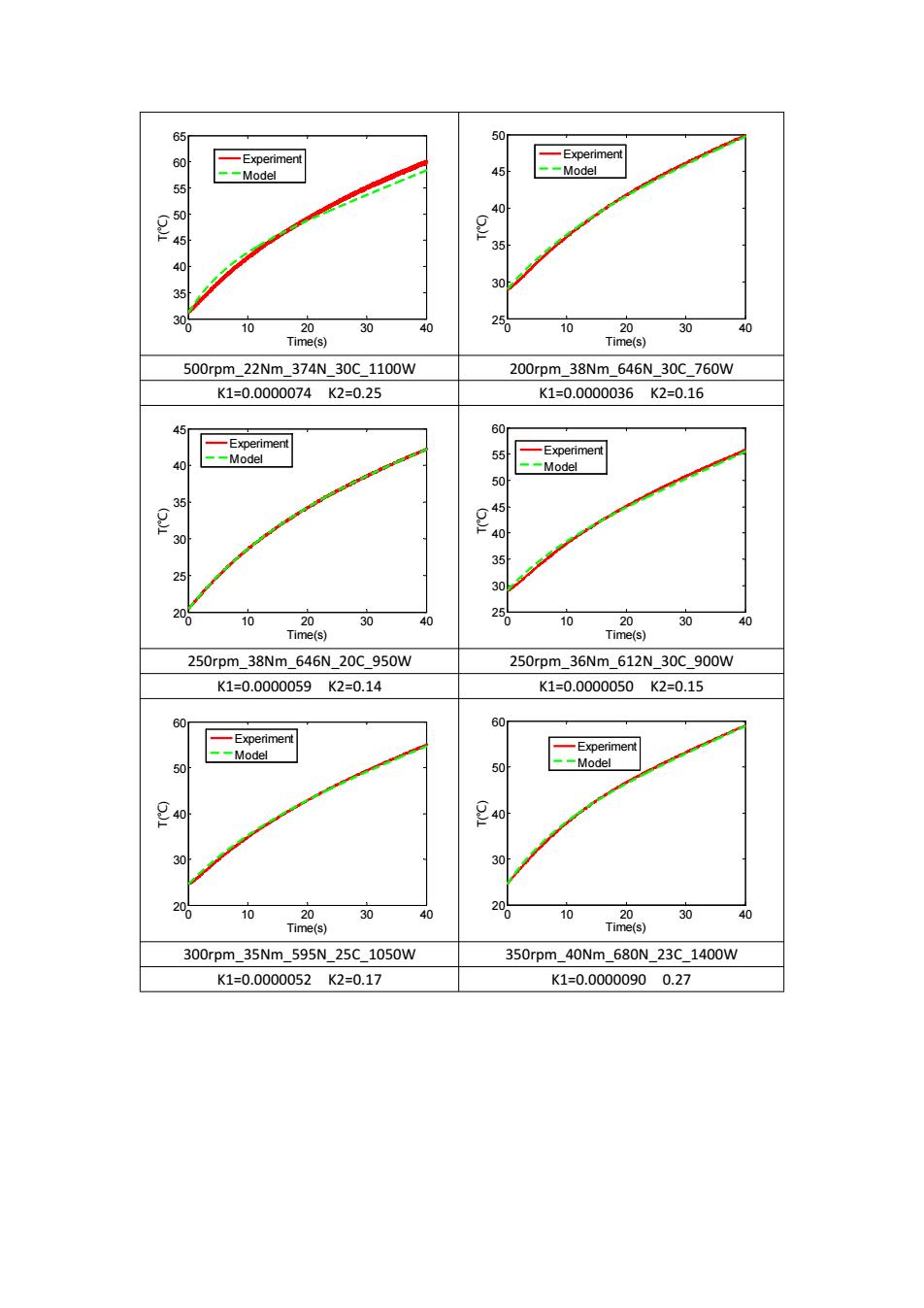
50 一Experiment -Experiment --Model AS --Model 55 50 40 45 35 30 35 10 20 30 40 % 10 20 30 40 Time(s) Time(s) 500rpm_22Nm_374N_30C_1100W 200rpm38Nm646N30C760W K1=0.0000074K2=0.25 K1=0.0000036K2=0.16 60 -Experiment 55 -Experiment 40 --Model --Model 50 45 30 35 25 30 o 10 20 30 40 10 20 30 40 Time(s) Time(s) 250rpm_38Nm_646N_20C950W 250rpm_36Nm612N_30C_900W K1=0.0000059K2=0.14 K1=0.0000050K2=0.15 60 60 -Experiment --Model -Experiment 50 -Model 30 30 200 10 20 30 40 10 20 30 40 Time(s) Time(s) 300rpm35Nm595N25C1050W 350rpm40Nm680N23C1400W K1=0.0000052K2=0.17 K1=0.00000900.27
0 10 20 30 40 30 35 40 45 50 55 60 65 Time(s) T(℃) Experiment Model 0 10 20 30 40 25 30 35 40 45 50 Time(s) T(℃) Experiment Model 500rpm_22Nm_374N_30C_1100W 200rpm_38Nm_646N_30C_760W K1=0.0000074 K2=0.25 K1=0.0000036 K2=0.16 0 10 20 30 40 20 25 30 35 40 45 Time(s) T(℃) Experiment Model 0 10 20 30 40 25 30 35 40 45 50 55 60 Time(s) T(℃) Experiment Model 250rpm_38Nm_646N_20C_950W 250rpm_36Nm_612N_30C_900W K1=0.0000059 K2=0.14 K1=0.0000050 K2=0.15 0 10 20 30 40 20 30 40 50 60 Time(s) T(℃) Experiment Model 0 10 20 30 40 20 30 40 50 60 Time(s) T(℃) Experiment Model 300rpm_35Nm_595N_25C_1050W 350rpm_40Nm_680N_23C_1400W K1=0.0000052 K2=0.17 K1=0.0000090 0.27
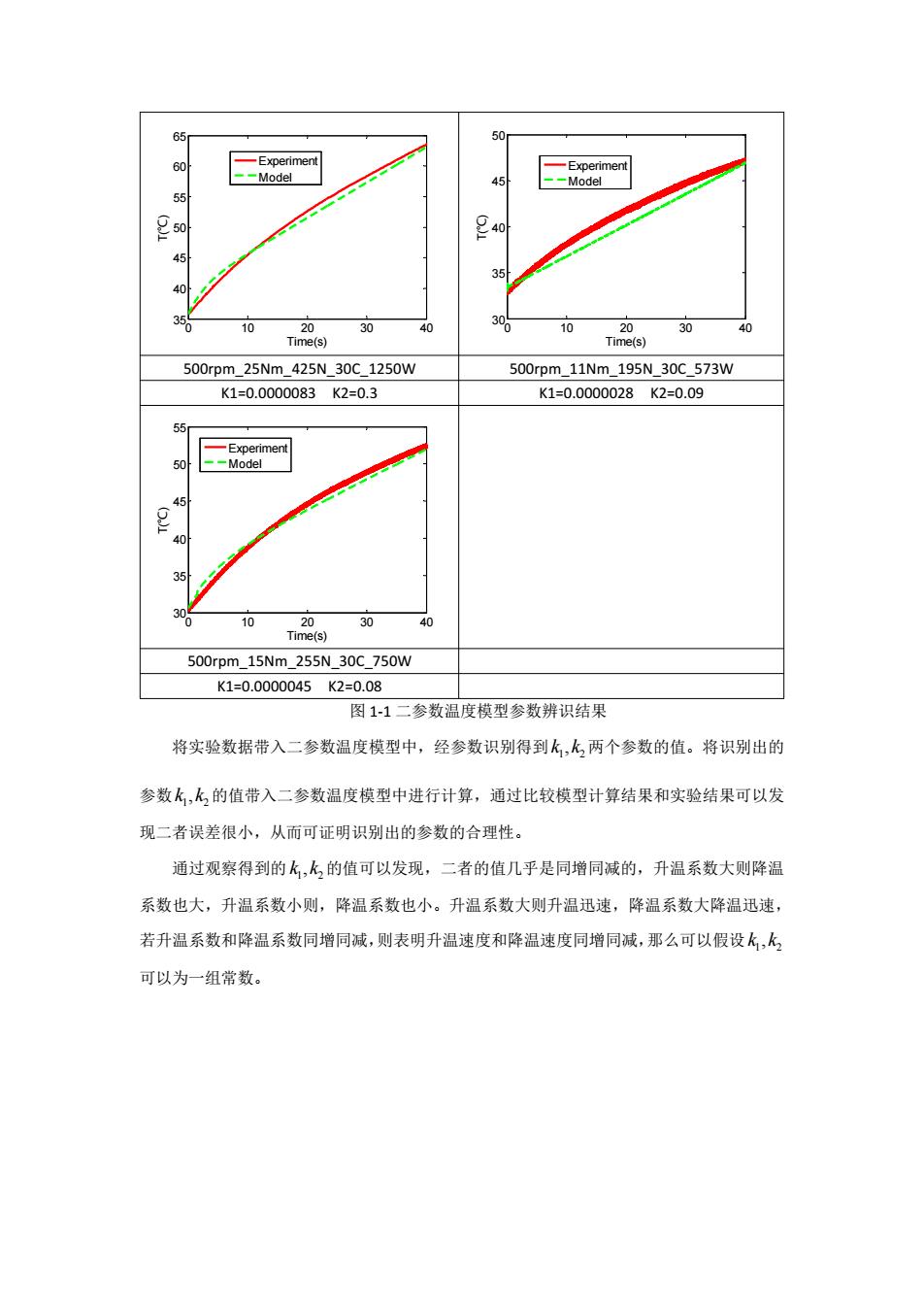
65 50 60 -Experiment -Experiment --Model 45 --Model 45 40 10 20 30 40 0 10 20 30 40 Time(s) Time(s) 500rpm_25Nm_425N_30C_1250W 500rpm11Nm195N30C573W K1=0.0000083K2=0.3 K1=0.0000028K2=0.09 55 -Experiment 50 --Model 45 90 35 30 0 10 20 30 40 Time(s) 500rpm15Nm255N_30C_750W K1=0.0000045K2=0.08 图1-1二参数温度模型参数辨识结果 将实验数据带入二参数温度模型中,经参数识别得到k,k,两个参数的值。将识别出的 参数k,k的值带入二参数温度模型中进行计算,通过比较模型计算结果和实验结果可以发 现二者误差很小,从而可证明识别出的参数的合理性。 通过观察得到的k,k的值可以发现,二者的值几乎是同增同减的,升温系数大则降温 系数也大,升温系数小则,降温系数也小。升温系数大则升温迅速,降温系数大降温迅速, 若升温系数和降温系数同增同减,则表明升温速度和降温速度同增同减,那么可以假设k,k 可以为一组常数
0 10 20 30 40 35 40 45 50 55 60 65 Time(s) T(℃) Experiment Model 0 10 20 30 40 30 35 40 45 50 Time(s) T(℃) Experiment Model 500rpm_25Nm_425N_30C_1250W 500rpm_11Nm_195N_30C_573W K1=0.0000083 K2=0.3 K1=0.0000028 K2=0.09 0 10 20 30 40 30 35 40 45 50 55 Time(s) T(℃) Experiment Model 500rpm_15Nm_255N_30C_750W K1=0.0000045 K2=0.08 图 1-1 二参数温度模型参数辨识结果 将实验数据带入二参数温度模型中,经参数识别得到 1 2 k ,k 两个参数的值。将识别出的 参数 1 2 k ,k 的值带入二参数温度模型中进行计算,通过比较模型计算结果和实验结果可以发 现二者误差很小,从而可证明识别出的参数的合理性。 通过观察得到的 1 2 k ,k 的值可以发现,二者的值几乎是同增同减的,升温系数大则降温 系数也大,升温系数小则,降温系数也小。升温系数大则升温迅速,降温系数大降温迅速, 若升温系数和降温系数同增同减,则表明升温速度和降温速度同增同减,那么可以假设 1 2 k ,k 可以为一组常数
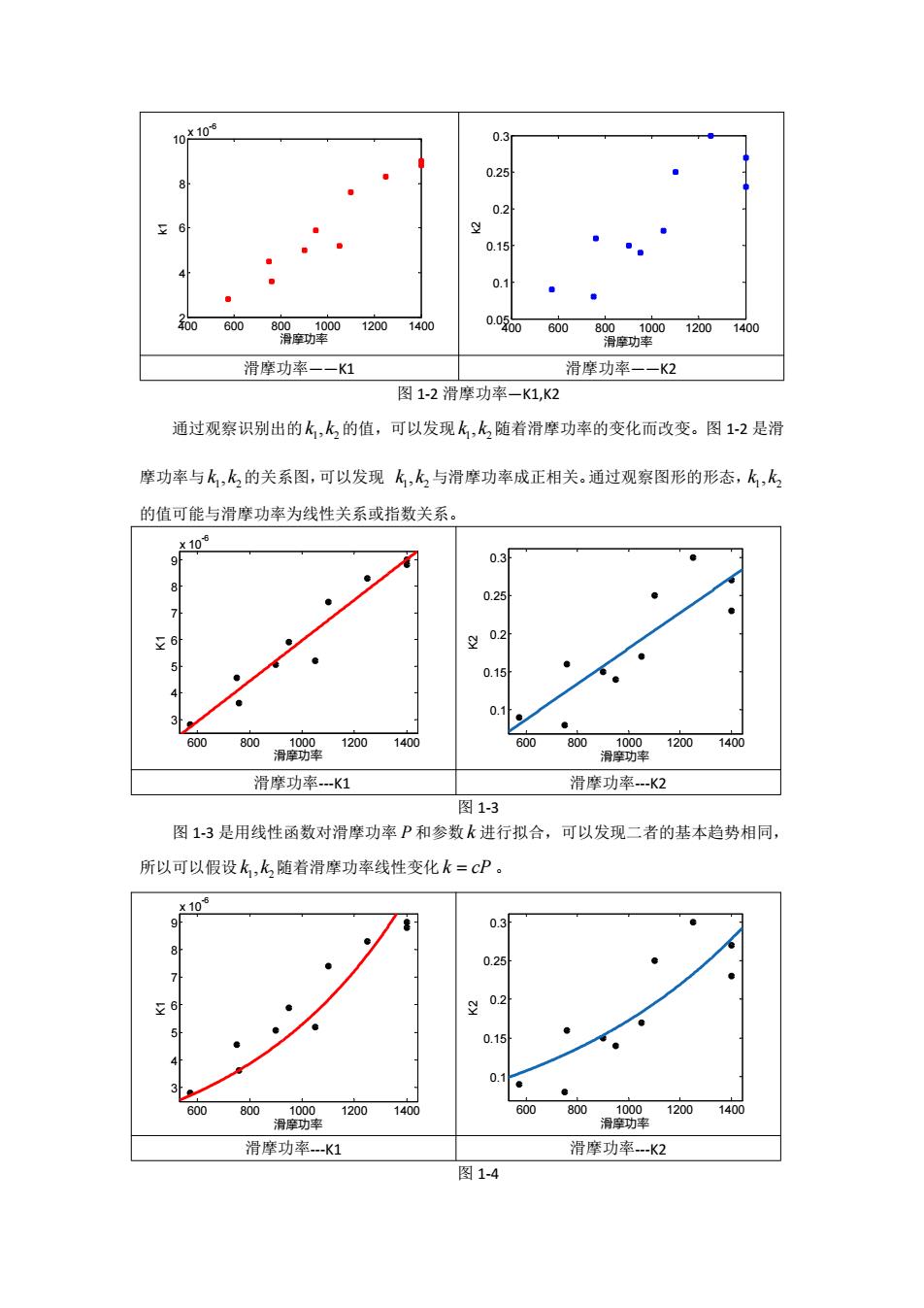
10'10s 0.25 0.2 ¥6 0.15 0.1 00 600 800 000 12001400 0.000 6008001000 12001400 滑摩功率 滑摩功率 滑摩功率一一K1 滑摩功率一一K2 图1-2滑摩功率一K1,K2 通过观察识别出的k,k的值,可以发现k,k随着滑摩功率的变化而改变。图1-2是滑 摩功率与k,的关系图,可以发现k,k与滑摩功率成正相关。通过观察图形的形态,k,k 的值可能与滑摩功率为线性关系或指数关系。 106 0.3 8 0.25 ¥6 义 0.2 0.15 0.1 ● 600 800 1000 1200 1400 600800100012001400 滑摩功率 滑摩功率 滑摩功率.-K1 滑摩功率-K2 图1-3 图13是用线性函数对滑摩功率P和参数k进行拟合,可以发现二者的基本趋势相同, 所以可以假设k,k随着滑摩功率线性变化k=cP。 106 9 0.3 0.25 6 义 0.2 0.15 0.1 600 800 1000 1200 1400 600 800 1000 12001400 滑摩功率 滑摩功率 滑摩功率.-K1 滑摩功率.-K2 图1-4
400 600 800 1000 1200 1400 2 4 6 8 10 x 10 -6 滑摩功率 k1 400 600 800 1000 1200 1400 0.05 0.1 0.15 0.2 0.25 0.3 k2 滑摩功率 滑摩功率——K1 滑摩功率——K2 图 1-2 滑摩功率—K1,K2 通过观察识别出的 1 2 k ,k 的值,可以发现 1 2 k ,k 随着滑摩功率的变化而改变。图 1-2 是滑 摩功率与 1 2 k ,k 的关系图,可以发现 1 2 k ,k 与滑摩功率成正相关。通过观察图形的形态, 1 2 k ,k 的值可能与滑摩功率为线性关系或指数关系。 600 800 1000 1200 1400 3 4 5 6 7 8 9 x 10 -6 滑摩功率 K1 600 800 1000 1200 1400 0.1 0.15 0.2 0.25 0.3 滑摩功率 K2 滑摩功率---K1 滑摩功率---K2 图 1-3 图 1-3 是用线性函数对滑摩功率 P 和参数 k 进行拟合,可以发现二者的基本趋势相同, 所以可以假设 1 2 k ,k 随着滑摩功率线性变化 k cP 。 600 800 1000 1200 1400 3 4 5 6 7 8 9 x 10 -6 滑摩功率 K1 600 800 1000 1200 1400 0.1 0.15 0.2 0.25 0.3 滑摩功率 K2 滑摩功率---K1 滑摩功率---K2 图 1-4
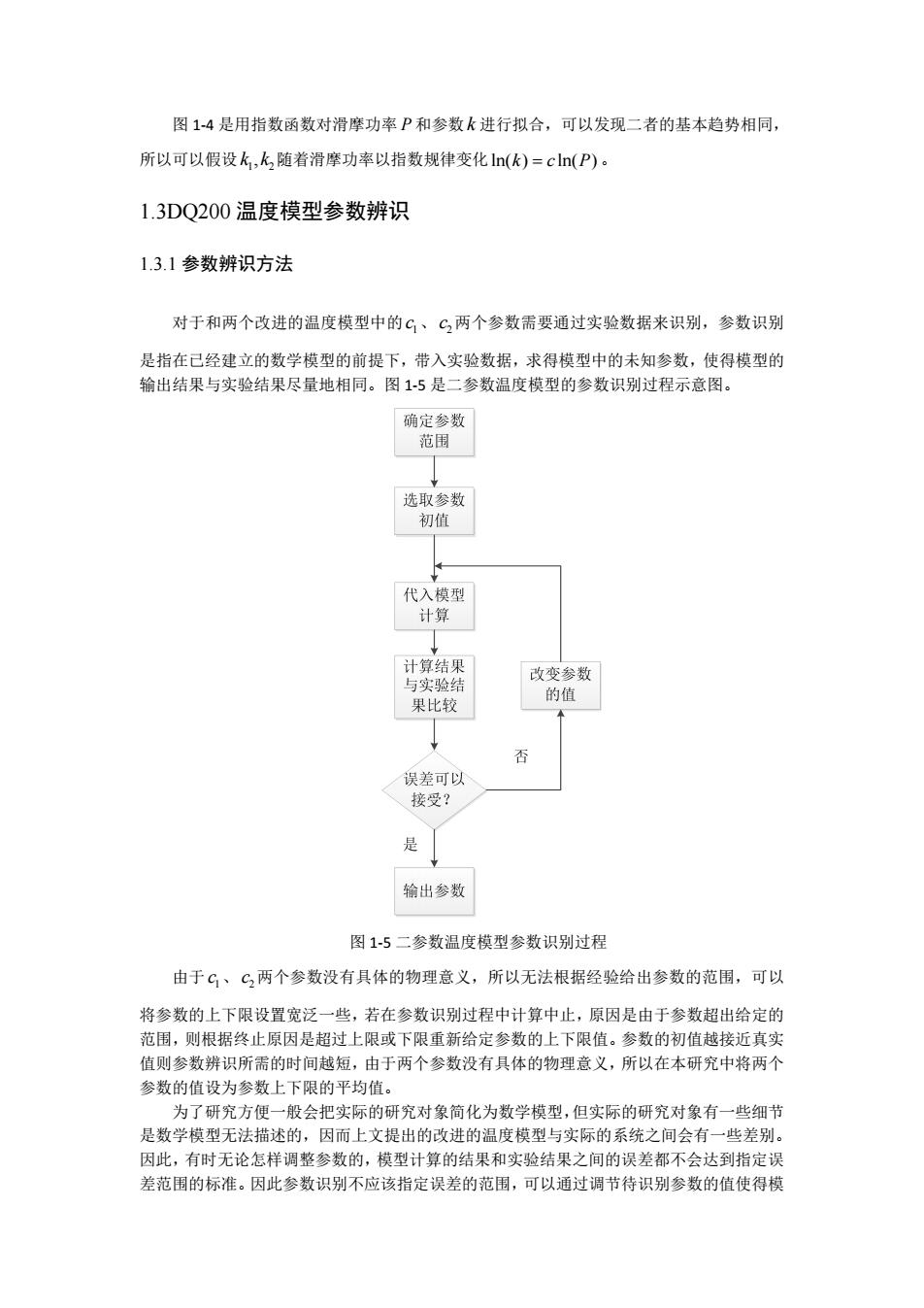
图1-4是用指数函数对滑摩功率P和参数k进行拟合,可以发现二者的基本趋势相同, 所以可以假设k,k,随着滑摩功率以指数规律变化ln(k)=cln(P)。 1.3DQ200温度模型参数辨识 1.3.1参数辨识方法 对于和两个改进的温度模型中的G、C,两个参数需要通过实验数据来识别,参数识别 是指在己经建立的数学模型的前提下,带入实验数据,求得模型中的未知参数,使得模型的 输出结果与实验结果尽量地相同。图1-5是二参数温度模型的参数识别过程示意图。 确定参数 范围 选取参数 初值 代入模型 计算 计算结果 与实验结 改变参数 果比较 的值 否 误差可以 接受? 浪 输出参数 图1-5二参数温度模型参数识别过程 由于G、C,两个参数没有具体的物理意义,所以无法根据经验给出参数的范围,可以 将参数的上下限设置宽泛一些,若在参数识别过程中计算中止,原因是由于参数超出给定的 范围,则根据终止原因是超过上限或下限重新给定参数的上下限值。参数的初值越接近真实 值则参数辨识所需的时间越短,由于两个参数没有具体的物理意义,所以在本研究中将两个 参数的值设为参数上下限的平均值。 为了研究方便一般会把实际的研究对象简化为数学模型,但实际的研究对象有一些细节 是数学模型无法描述的,因而上文提出的改进的温度模型与实际的系统之间会有一些差别。 因此,有时无论怎样调整参数的,模型计算的结果和实验结果之间的误差都不会达到指定误 差范围的标准。因此参数识别不应该指定误差的范围,可以通过调节待识别参数的值使得模
图 1-4 是用指数函数对滑摩功率 P 和参数 k 进行拟合,可以发现二者的基本趋势相同, 所以可以假设 1 2 k ,k 随着滑摩功率以指数规律变化 ln(k) c ln(P) 。 1.3DQ200 温度模型参数辨识 1.3.1 参数辨识方法 对于和两个改进的温度模型中的 1c 、 2 c 两个参数需要通过实验数据来识别,参数识别 是指在已经建立的数学模型的前提下,带入实验数据,求得模型中的未知参数,使得模型的 输出结果与实验结果尽量地相同。图 1-5 是二参数温度模型的参数识别过程示意图。 图 1-5 二参数温度模型参数识别过程 由于 1c 、 2 c 两个参数没有具体的物理意义,所以无法根据经验给出参数的范围,可以 将参数的上下限设置宽泛一些,若在参数识别过程中计算中止,原因是由于参数超出给定的 范围,则根据终止原因是超过上限或下限重新给定参数的上下限值。参数的初值越接近真实 值则参数辨识所需的时间越短,由于两个参数没有具体的物理意义,所以在本研究中将两个 参数的值设为参数上下限的平均值。 为了研究方便一般会把实际的研究对象简化为数学模型,但实际的研究对象有一些细节 是数学模型无法描述的,因而上文提出的改进的温度模型与实际的系统之间会有一些差别。 因此,有时无论怎样调整参数的,模型计算的结果和实验结果之间的误差都不会达到指定误 差范围的标准。因此参数识别不应该指定误差的范围,可以通过调节待识别参数的值使得模

型计算结果和实验结果之间的误差最小。 干式离合器温度模型的参数识别过程实际是带有约束的优化过程,带有约束是指给定的 参数范围。本研究采用MATLAB中的Isqnonlin非线性拟合函数完成参数辨识,其原理是 最小二乘法,不断地改变待识别的参数的值从而找到合适的参数值使得在有相同的输入值的 条件下,模型的计算结果和实验结果的方差最小。优化过程的示意图如图1-6所示。 初始化 调用 simulink 模型 迭代 终止 否 条件? 是 输出参数 图1-6优化过程的思路 初始化是指设定待识别参数的范围及为待识别的参数赋初值:调用的simulink模型是指 改进的温度模型,输入是离合器的转速差,滑摩转矩,通过MATLAB中的lookup模块输入 模型,输出是模型的计算结果和实验结果的差值。当满足终止条件时,停止迭代,输出参数 值,当不满足终止条件时则重新选择参数值进行计算直到满足终止条件输出参数值。这里的 终止条件包括待识别参数的变化量、模型计算结果和实验结果的方差的改变量,以及迭代的 次数。 1.3.2在MATLAB中实现最小二乘法参数辨识 k0=[11]: options optimoptions('Isqnonlin'); options.TolFun 1e-10; options.TolX le-10; options.MaxIter 400: options.MaxFunEvals 40000: dowm=[0.00000000000010.000000000001]: up=[10050000000000000000000000000]: [k,fx]1sqnonlin(@func_zpf,k0,down,up,options); 图1-7参数识别程序 在上述的程序中,k0是指待识别参数的初始值,若初始值与目标值比较接近则可以使
型计算结果和实验结果之间的误差最小。 干式离合器温度模型的参数识别过程实际是带有约束的优化过程,带有约束是指给定的 参数范围。本研究采用 MATLAB 中的 1sqnonlin 非线性拟合函数完成参数辨识,其原理是 最小二乘法,不断地改变待识别的参数的值从而找到合适的参数值使得在有相同的输入值的 条件下,模型的计算结果和实验结果的方差最小。优化过程的示意图如图 1-6 所示。 图 1-6 优化过程的思路 初始化是指设定待识别参数的范围及为待识别的参数赋初值;调用的 simulink 模型是指 改进的温度模型,输入是离合器的转速差,滑摩转矩,通过 MATLAB 中的 lookup 模块输入 模型,输出是模型的计算结果和实验结果的差值。当满足终止条件时,停止迭代,输出参数 值,当不满足终止条件时则重新选择参数值进行计算直到满足终止条件输出参数值。这里的 终止条件包括待识别参数的变化量、模型计算结果和实验结果的方差的改变量,以及迭代的 次数。 1.3.2 在 MATLAB 中实现最小二乘法参数辨识 图1-7参数识别程序 在上述的程序中,k0 是指待识别参数的初始值,若初始值与目标值比较接近则可以使
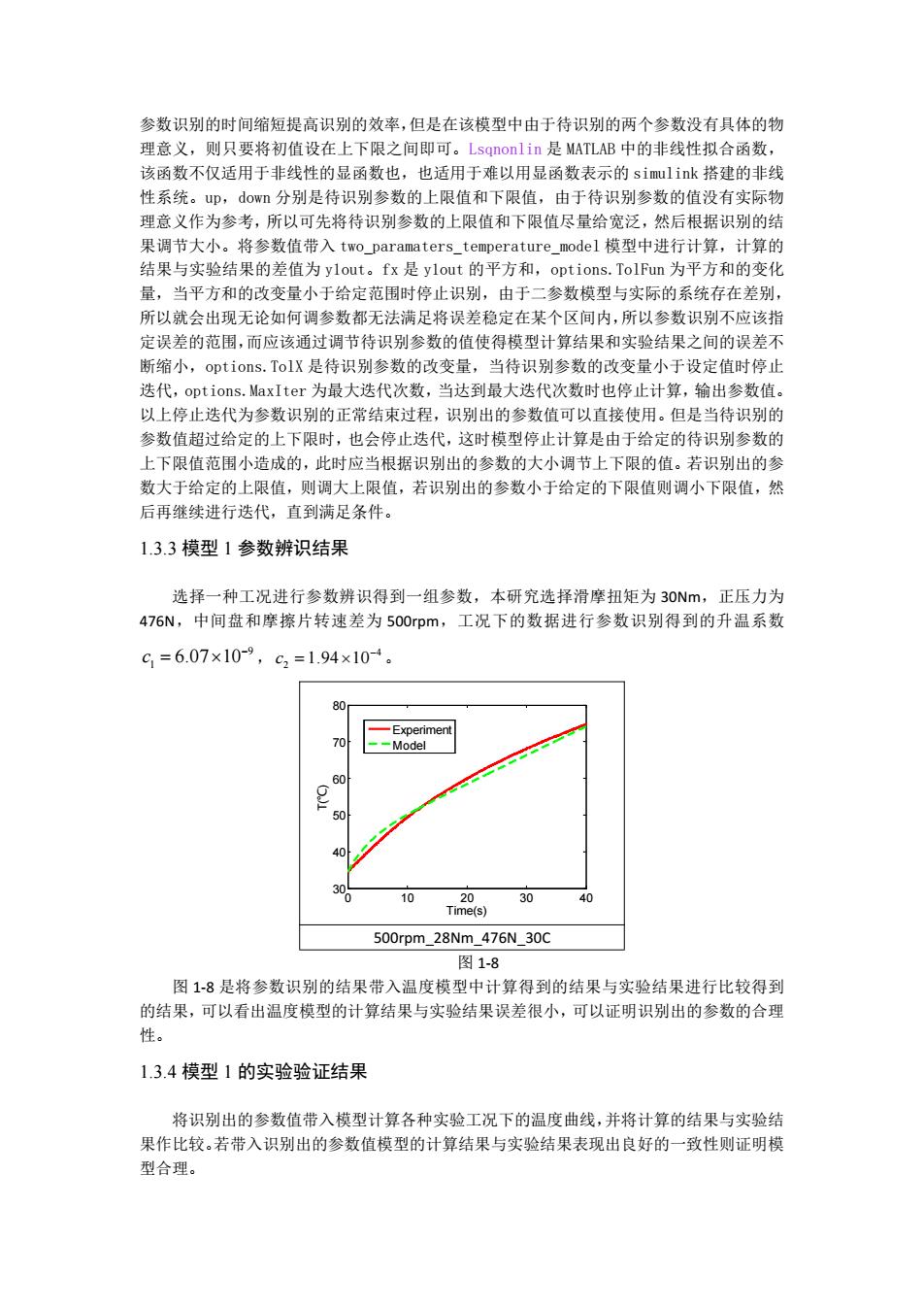
参数识别的时间缩短提高识别的效率,但是在该模型中由于待识别的两个参数没有具体的物 理意义,则只要将初值设在上下限之间即可。Lsqnonlin是MATLAB中的非线性拟合函数, 该函数不仅适用于非线性的显函数也,也适用于难以用显函数表示的simulink搭建的非线 性系统。up,down分别是待识别参数的上限值和下限值,由于待识别参数的值没有实际物 理意义作为参考,所以可先将待识别参数的上限值和下限值尽量给宽泛,然后根据识别的结 果调节大小。将参数值带入two_paramaters_temperature_model模型中进行计算,计算的 结果与实验结果的差值为ylout。.fx是ylout的平方和,options.TolFun为平方和的变化 量,当平方和的改变量小于给定范围时停止识别,由于二参数模型与实际的系统存在差别, 所以就会出现无论如何调参数都无法满足将误差稳定在某个区间内,所以参数识别不应该指 定误差的范围,而应该通过调节待识别参数的值使得模型计算结果和实验结果之间的误差不 断缩小,options.TolX是待识别参数的改变量,当待识别参数的改变量小于设定值时停止 迭代,options.MaxIter为最大迭代次数,当达到最大迭代次数时也停止计算,输出参数值。 以上停止迭代为参数识别的正常结束过程,识别出的参数值可以直接使用。但是当待识别的 参数值超过给定的上下限时,也会停止迭代,这时模型停止计算是由于给定的待识别参数的 上下限值范围小造成的,此时应当根据识别出的参数的大小调节上下限的值。若识别出的参 数大于给定的上限值,则调大上限值,若识别出的参数小于给定的下限值则调小下限值,然 后再继续进行迭代,直到满足条件。 1.3.3模型1参数辨识结果 选择一种工况进行参数辨识得到一组参数,本研究选择滑摩扭矩为30Nm,正压力为 476N,中间盘和摩擦片转速差为500rpm,工况下的数据进行参数识别得到的升温系数 c=6.07×10-9,c2=1.94×10-4。 80 -Experiment 70 --Model 60 50 40 10 20 30 40 Time(s) 500rpm 28Nm 476N 30C 图1-8 图1-8是将参数识别的结果带入温度模型中计算得到的结果与实验结果进行比较得到 的结果,可以看出温度模型的计算结果与实验结果误差很小,可以证明识别出的参数的合理 性。 1.3.4模型1的实验验证结果 将识别出的参数值带入模型计算各种实验工况下的温度曲线,并将计算的结果与实验结 果作比较。若带入识别出的参数值模型的计算结果与实验结果表现出良好的一致性则证明模 型合理
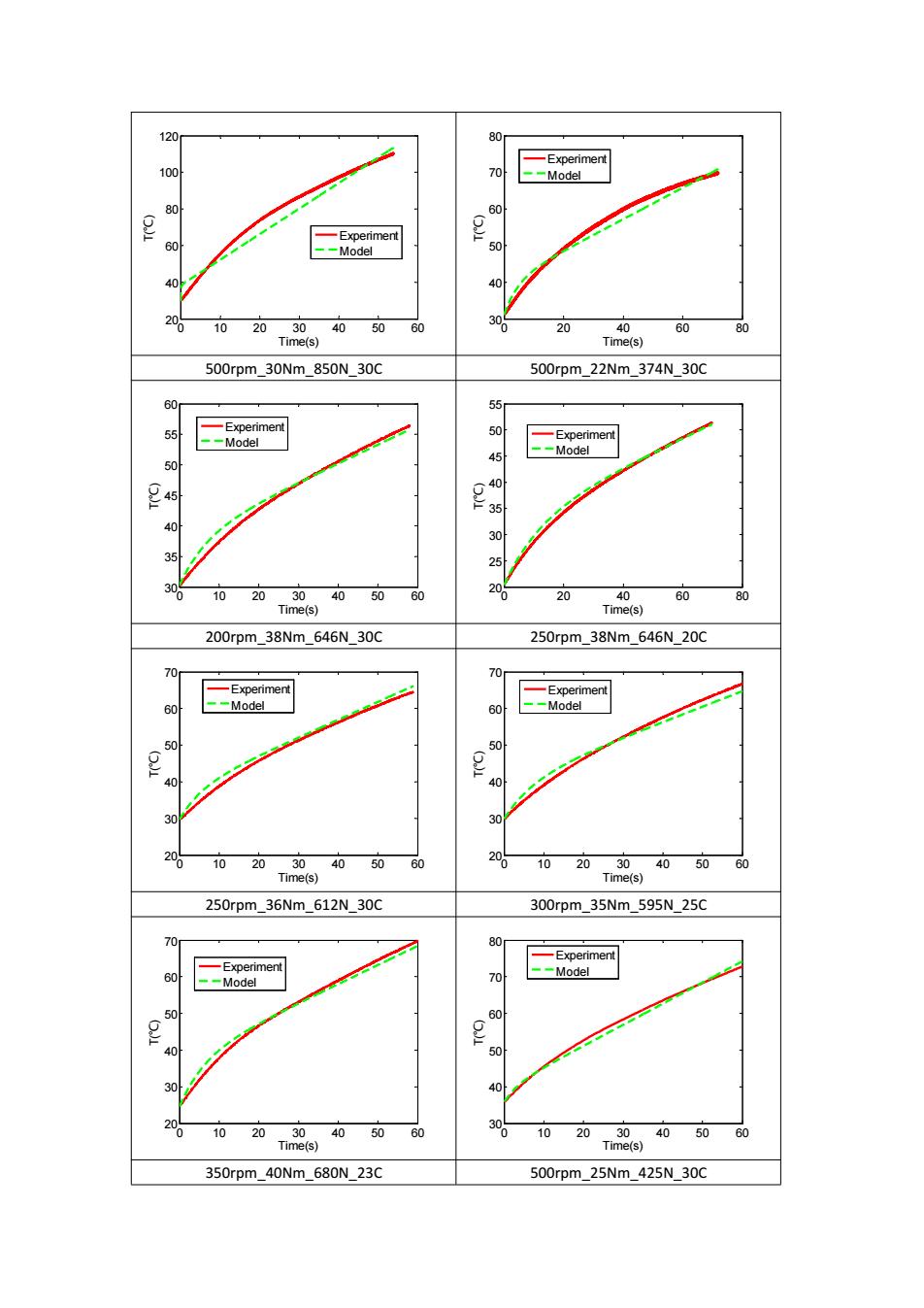
参数识别的时间缩短提高识别的效率,但是在该模型中由于待识别的两个参数没有具体的物 理意义,则只要将初值设在上下限之间即可。Lsqnonlin 是 MATLAB 中的非线性拟合函数, 该函数不仅适用于非线性的显函数也,也适用于难以用显函数表示的 simulink 搭建的非线 性系统。up,down 分别是待识别参数的上限值和下限值,由于待识别参数的值没有实际物 理意义作为参考,所以可先将待识别参数的上限值和下限值尽量给宽泛,然后根据识别的结 果调节大小。将参数值带入 two_paramaters_temperature_model 模型中进行计算,计算的 结果与实验结果的差值为 y1out。fx 是 y1out 的平方和,options.TolFun 为平方和的变化 量,当平方和的改变量小于给定范围时停止识别,由于二参数模型与实际的系统存在差别, 所以就会出现无论如何调参数都无法满足将误差稳定在某个区间内,所以参数识别不应该指 定误差的范围,而应该通过调节待识别参数的值使得模型计算结果和实验结果之间的误差不 断缩小,options.TolX 是待识别参数的改变量,当待识别参数的改变量小于设定值时停止 迭代,options.MaxIter 为最大迭代次数,当达到最大迭代次数时也停止计算,输出参数值。 以上停止迭代为参数识别的正常结束过程,识别出的参数值可以直接使用。但是当待识别的 参数值超过给定的上下限时,也会停止迭代,这时模型停止计算是由于给定的待识别参数的 上下限值范围小造成的,此时应当根据识别出的参数的大小调节上下限的值。若识别出的参 数大于给定的上限值,则调大上限值,若识别出的参数小于给定的下限值则调小下限值,然 后再继续进行迭代,直到满足条件。 1.3.3 模型 1 参数辨识结果 选择一种工况进行参数辨识得到一组参数,本研究选择滑摩扭矩为 30Nm,正压力为 476N,中间盘和摩擦片转速差为 500rpm,工况下的数据进行参数识别得到的升温系数 9 1 c 6.07 10 , 4 2 c 1.94 10 。 0 10 20 30 40 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 500rpm_28Nm_476N_30C 图 1-8 图 1-8 是将参数识别的结果带入温度模型中计算得到的结果与实验结果进行比较得到 的结果,可以看出温度模型的计算结果与实验结果误差很小,可以证明识别出的参数的合理 性。 1.3.4 模型 1 的实验验证结果 将识别出的参数值带入模型计算各种实验工况下的温度曲线,并将计算的结果与实验结 果作比较。若带入识别出的参数值模型的计算结果与实验结果表现出良好的一致性则证明模 型合理
120 一Experiment 100 70 --Model 60 -Experiment 60 --Model 50 40 40 20% 102030405060 20 40 60 80 Time(s) Time(s) 500rpm30Nm_850N_30C 500rpm_22Nm_374N_30C 60 吸 55 一Experiment 50 --Model -Experiment 45 --Model 40 40 30 35 25 300 10 2030405060 200 20 40 6080 Time(s) Time(s) 200rpm 38Nm 646N 30C 250rpm 38Nm 646N 20C 10 0 一Experiment -Experiment % --Model 60 --Model 50 50 40 40 30 200 0 2030405060 206 10 2030405060 Time(s) Time(s) 250rpm 36Nm 612N 30C 300rpm 35Nm 595N 25C 70 80 -Experiment 一Experiment 60 --Model 70 --Model 50 60H 40 50 30 40 102030 405060 o 102030 405060 Time(s) Time(s) 350rpm_40Nm_680N_23C 500rpm_25Nm425N30c
0 10 20 30 40 50 60 20 40 60 80 100 120 Time(s) T(℃) Experiment Model 0 20 40 60 80 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 500rpm_30Nm_850N_30C 500rpm_22Nm_374N_30C 0 10 20 30 40 50 60 30 35 40 45 50 55 60 Time(s) T(℃) Experiment Model 0 20 40 60 80 20 25 30 35 40 45 50 55 Time(s) T(℃) Experiment Model 200rpm_38Nm_646N_30C 250rpm_38Nm_646N_20C 0 10 20 30 40 50 60 20 30 40 50 60 70 Time(s) T(℃) Experiment Model 0 10 20 30 40 50 60 20 30 40 50 60 70 Time(s) T(℃) Experiment Model 250rpm_36Nm_612N_30C 300rpm_35Nm_595N_25C 0 10 20 30 40 50 60 20 30 40 50 60 70 Time(s) T(℃) Experiment Model 0 10 20 30 40 50 60 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 350rpm_40Nm_680N_23C 500rpm_25Nm_425N_30C
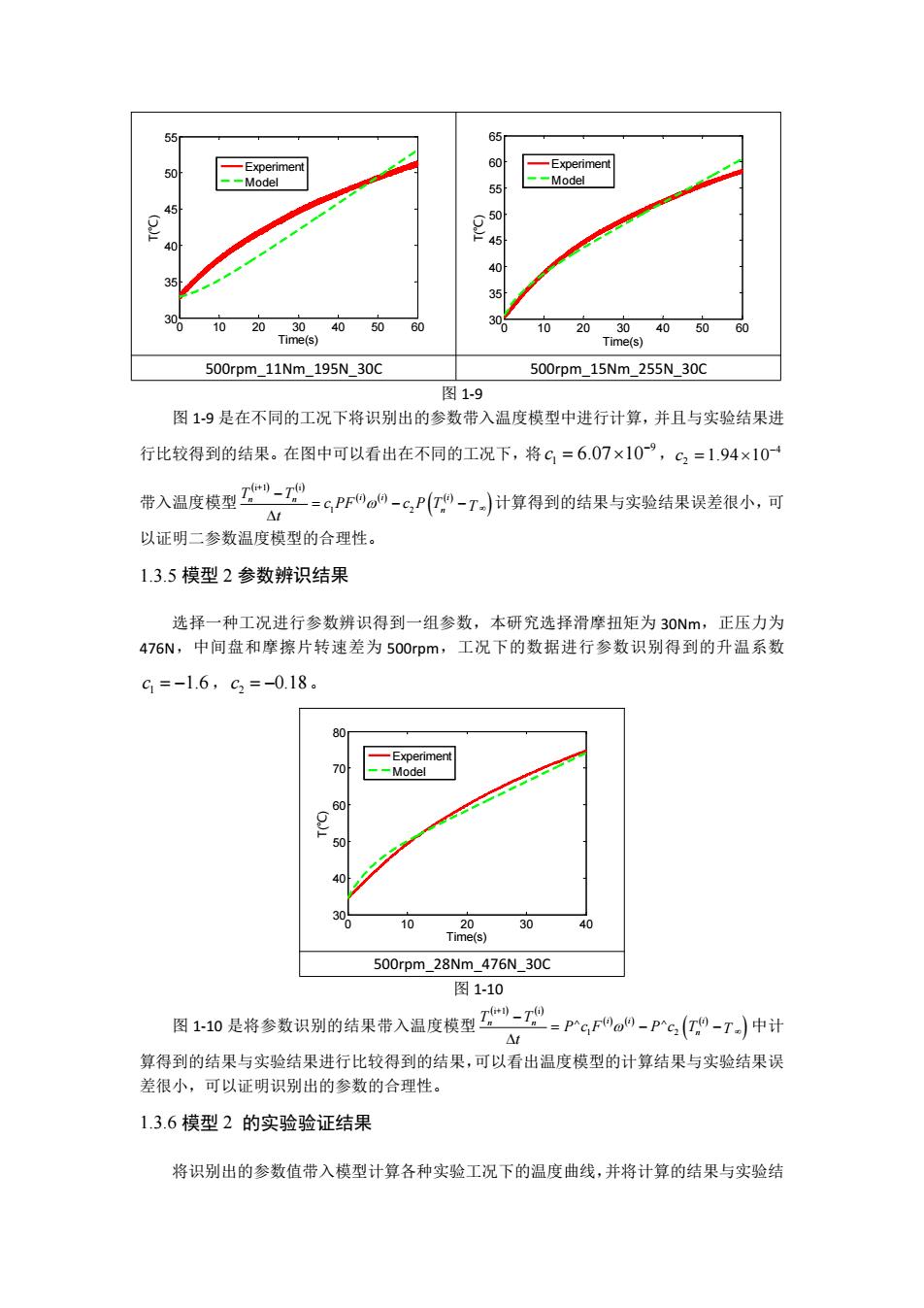
55 65r 50 一Experiment -Experiment --Model 55 --Model 45 40 45 40 35 35 102030 4050.60 30 102030405060 Time(s) Time(s) 500rpm_11Nm_195N_30C 500rpm_15Nm_255N_30C 图1-9 图1-9是在不同的工况下将识别出的参数带入温度模型中进行计算,并且与实验结果进 行比较得到的结果。在图中可以看出在不同的工况下,将C=6.07×10”,62=1.94×10 带入温度模型-7 =cPFo0-c,P(T-T)计算得到的结果与实验结果误差很小,可 △t 以证明二参数温度模型的合理性。 1.3.5模型2参数辨识结果 选择一种工况进行参数辨识得到一组参数,本研究选择滑摩扭矩为30Nm,正压力为 476N,中间盘和摩擦片转速差为500rpm,工况下的数据进行参数识别得到的升温系数 C=-1.6,c2=-0.18。 80 -Experiment 70 --Model 60 50 40 10 20 30 40 Time(s) 500rpm 28Nm 476N 30C 图1-10 图1:10是将参数识别的结果带入温度模型",:PcF-P%(0-7中计 △t 算得到的结果与实验结果进行比较得到的结果,可以看出温度模型的计算结果与实验结果误 差很小,可以证明识别出的参数的合理性。 1.3.6模型2的实验验证结果 将识别出的参数值带入模型计算各种实验工况下的温度曲线,并将计算的结果与实验结
0 10 20 30 40 50 60 30 35 40 45 50 55 Time(s) T(℃) Experiment Model 0 10 20 30 40 50 60 30 35 40 45 50 55 60 65 Time(s) T(℃) Experiment Model 500rpm_11Nm_195N_30C 500rpm_15Nm_255N_30C 图 1-9 图 1-9 是在不同的工况下将识别出的参数带入温度模型中进行计算,并且与实验结果进 行比较得到的结果。在图中可以看出在不同的工况下,将 9 1 c 6.07 10 , 4 2 c 1.94 10 带入温度模型 i+1 i 1 2 n n i i i n T T c PF c P T T t 计算得到的结果与实验结果误差很小,可 以证明二参数温度模型的合理性。 1.3.5 模型 2 参数辨识结果 选择一种工况进行参数辨识得到一组参数,本研究选择滑摩扭矩为 30Nm,正压力为 476N,中间盘和摩擦片转速差为 500rpm,工况下的数据进行参数识别得到的升温系数 1 c 1.6 , 2 c 0.18。 0 10 20 30 40 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 500rpm_28Nm_476N_30C 图 1-10 图 1-10 是将参数识别的结果带入温度模型 i+1 i 1 2 n n i i i n T T P c F P c T T t 中计 算得到的结果与实验结果进行比较得到的结果,可以看出温度模型的计算结果与实验结果误 差很小,可以证明识别出的参数的合理性。 1.3.6 模型 2 的实验验证结果 将识别出的参数值带入模型计算各种实验工况下的温度曲线,并将计算的结果与实验结