
第十二章动载荷 ▣概述 ▣惯性力问题 ▣冲击应力与变形 ▣提高构件动强度的措施 ▣ *冲击韧度 西半氕通大率 航天航空学院一力学中心 XIAN JIAOTONG UNIVERSITY
第十二章 动载荷 概述 惯性力问题 冲击应力与变形 提高构件动强度的措施 *冲击韧度 航天航空学院--力学中心

12-1概述 静载荷:载荷由零缓慢增加,到达某值后保持不变; (Static loading) 动载荷:引起构件加速度的载荷或冲击载荷; (Dynamic loading) 动变形和动应力:在动载荷下产生的变形和应力; 惯性力问题:已知加速度 冲击问题:未知加速度(能量守衡) 动载荷问题分类: 疲劳问题:持续变化的载荷作用 振动问题:(不涉及) 研究基本假设:动载荷作用下,应力、应变保持线性关系
12-1 概述 静载荷: (Static loading) 动载荷: (Dynamic loading) 动变形和动应力: 研究基本假设:动载荷作用下,应力、应变保持线性关系。 载荷由零缓慢增加,到达某值后保持不变; 引起构件加速度的载荷或冲击载荷; 在动载荷下产生的变形和应力; 动载荷问题分类: 惯性力问题:已知加速度 冲击问题:未知加速度(能量守衡) 疲劳问题:持续变化的载荷作用 振动问题:(不涉及)
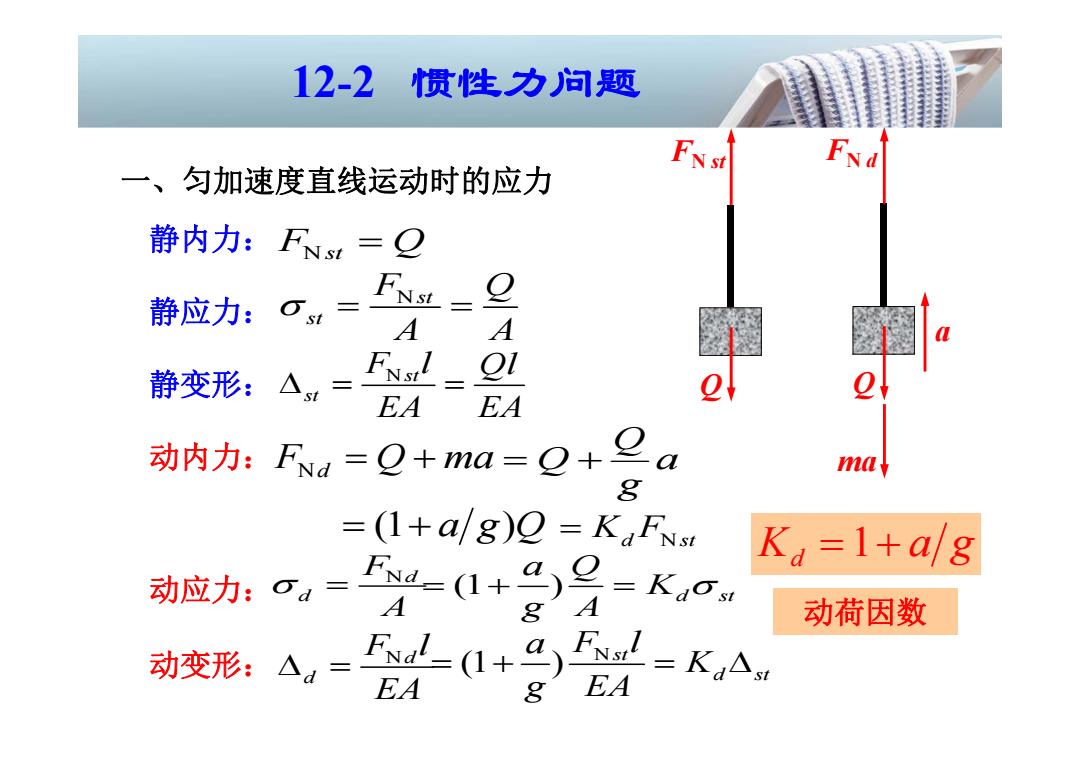
12-2, 惯性力问题 Fxd 一、匀加速度直线运动时的应力 静内力:FNs1=Q 静应力:O1= A A Ol 静变形:△ EA EA 动内力:Ra=Q+ma=o+ a may 8 =(1+a/g)O=KaFNs Kd=1+a/g 动应力:od= A 8 动荷因数 EA 81 EA
一、匀加速度直线运动时的应力 N d d F A K d 1 a g 动荷因数 FN d Q ma a g Q Q ( 1 a g ) Q FNst Q Nst st F Q A A Nst st F l Ql EA EA 静内力: 静应力: 静变形: 动内力: 动应力: 动变形: K Fd st N N d d F l EA 12-2 惯性力问题 (1 ) d st a Q K g A N (1 ) st d st a F l K g EA FN st Q FN d Q a ma

12-2 惯性力问题 Kd d 动荷因数:动内力与静内力之比; 动应力与静应力之比: 动变形与静变形之比。 由于构件在静载荷作用下的内力、应力和变形的计 算已经掌握,所以在此基础上计算出动荷因数,就可以 求解动内力、动应力和动变形了。所以,解决动载荷问 题的关键是确定动荷因数
12-2 惯性力问题 动荷因数:动内力与静内力之比; 动应力与静应力之比; 动变形与静变形之比。 N N ddd d st st st F K F 由于构件在静载荷作用下的内力、应力和变形的计 算已经掌握,所以在此基础上计算出动荷因数,就可以 求解动内力、动应力和动变形了。所以,解决动载荷问 题的关键是确定动荷因数
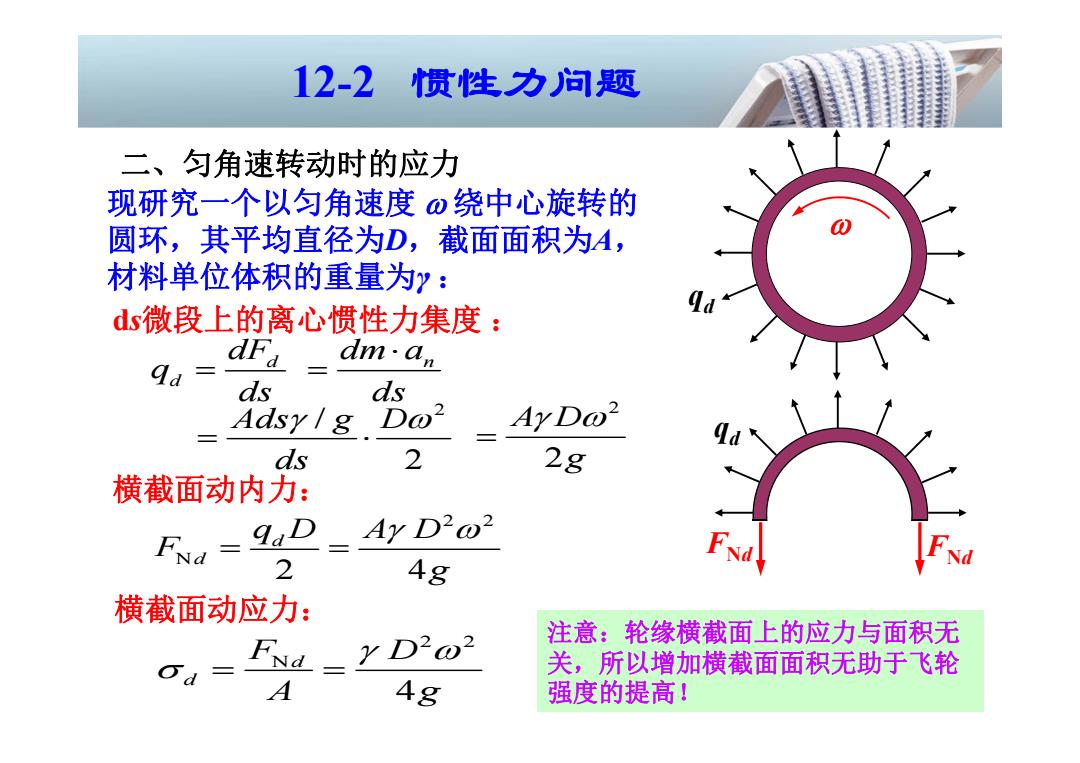
12-2 惯性力问题 二、匀角速转动时的应力 现研究一个以匀角速度0绕中心旋转的 圆环,其平均直径为D,截面面积为A, 材料单位体积的重量为?: ds微段上的离心惯性力集度: dFa dm·an 二 ds ds Adsy/g .Do? AyDo ds 2 2g 横截面动内力: Ay D2o2 2 Ag 横截面动应力: YD202 注意:轮缘横截面上的应力与面积无 od= FNd 关,所以增加横截面面积无助于飞轮 A 4g 强度的提高!
q d 二、匀角速转动时的应力 12-2 惯性力问题 d d dF q ds 2 2 N 2 4 d d q D A D F g 2 2 N 4 d d F D A g 现研究一个以匀角速度 绕中心旋转的 圆环,其平均直径为 D,截面面积为A , 材料单位体积的重量为 γ : 注意:轮缘横截面上的应力与面积无 关,所以增加横截面面积无助于飞轮 强度的提高! 2 / 2 Ads g D ds dm a n ds 2 2 A D g d s微段上的离心惯性力集度 : 横截面动内力: 横截面动应力: q d FN d FN d
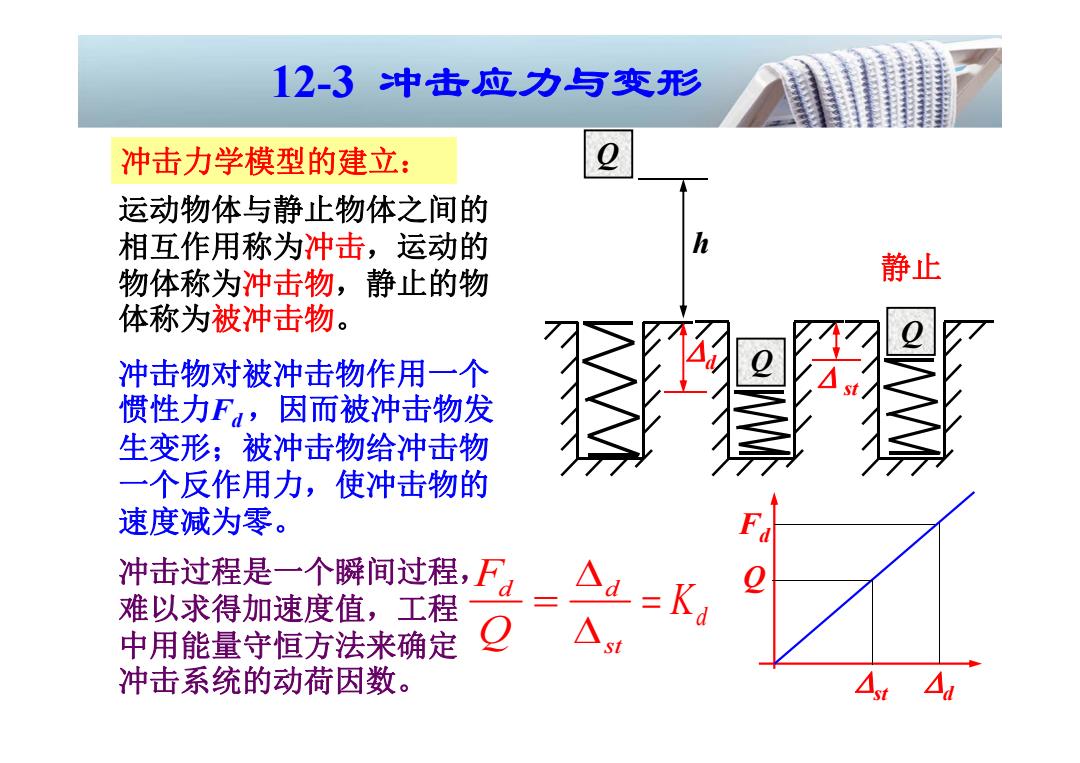
12-3冲击应力与变形 冲击力学模型的建立: 运动物体与静止物体之间的 相互作用称为冲击,运动的 h 物体称为冲击物,静止的物 静止 体称为被冲击物。 冲击物对被冲击物作用一个 惯性力F,因而被冲击物发 生变形;被冲击物给冲击物 一个反作用力,使冲击物的 速度减为零。 冲击过程是一个瞬间过程,F 难以求得加速度值,工程 Kd 中用能量守恒方法来确定 冲击系统的动荷因数
运动物体与静止物体之间的 相互作用称为冲击,运动的 物体称为冲击物,静止的物 体称为被冲击物 。 冲击物对被冲击物作用一个 惯性力 Fd ,因而被冲击物发 生变形;被冲击物给冲击物 一个反作用力,使冲击物的 速度减为零。 d d s t F Q K d 冲击过程是一个瞬间过程, 难以求得加速度值,工程 中用能量守恒方法来确定 冲击系统的动荷因数。 12-3 冲击应力与变形 Q h Q st 静止 Q d Fd d Q st 冲击力学模型的建立:
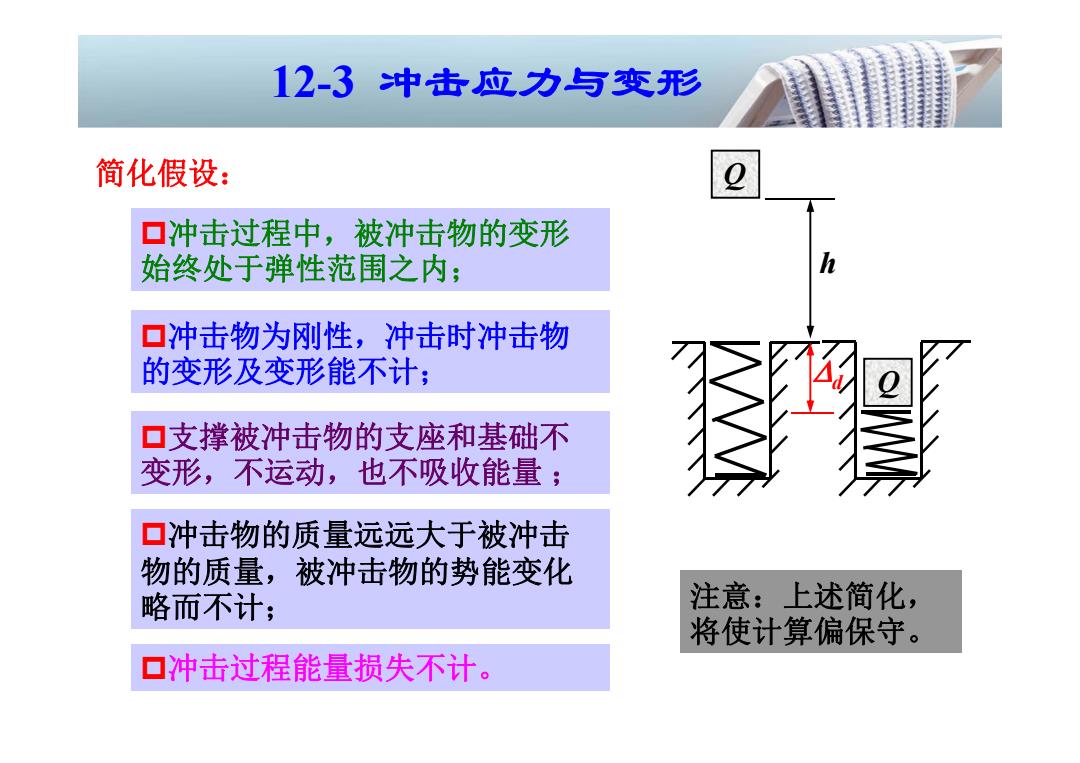
12-3冲击应力与变形 简化假设: 口冲击过程中,被冲击物的变形 始终处于弹性范围之内; ▣冲击物为刚性,冲击时冲击物 的变形及变形能不计; 口支撑被冲击物的支座和基础不 变形,不运动,也不吸收能量; 口冲击物的质量远远大于被冲击 物的质量,被冲击物的势能变化 略而不计; 注意:上述简化, 将使计算偏保守。 口冲击过程能量损失不计
简化假设: 冲击物为刚性,冲击时冲击物 的变形及变形能不计; 冲击过程中,被冲击物的变形 始终处于弹性范围之内; 支撑被冲击物的支座和基础不 变形,不运动,也不吸收能量 ; 冲击物的质量远远大于被冲击 物的质量,被冲击物的势能变化 略而不计; 冲击过程能量损失不计。 12-3 冲击应力与变形 Q h d Q 注意:上述简化, 将使计算偏保守
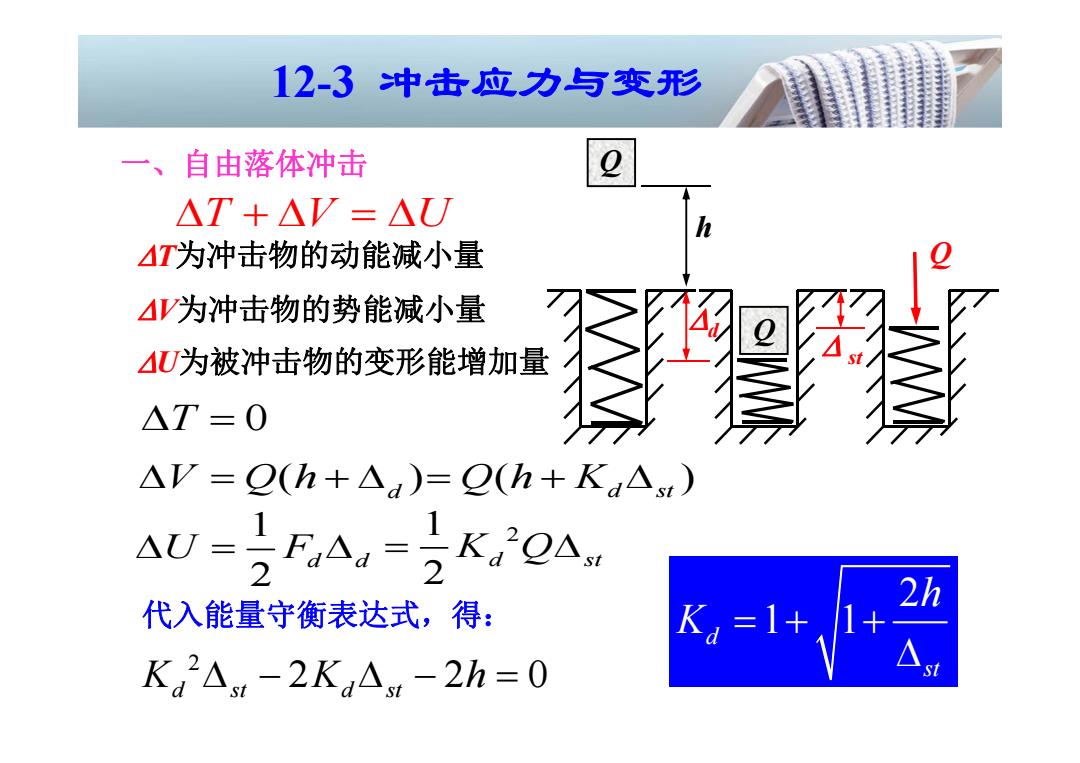
12-3冲击应力与变形 一、 自由落体冲击 △T+△V=△ T为冲击物的动能减小量 么V为冲击物的势能减小量 U为被冲击物的变形能增加量 △T=0 △V=Q(h+△a)=Q(h+Ka△t) AU-TFA-IKQA 2h 代入能量守衡表达式,得: Kg=1+ 1+ Ka△t-2Ka△t-2h=0 4
一、自由落体冲击 T V U T为冲击物的动能减小量 V为冲击物的势能减小量 U为被冲击物的变形能增加量 T 0 ( ) V Qh d 1 2 U Fd d 2 2 20 K Kh d st d st 代入能量守衡表达式,得: 2 1 1 d st h K ( ) Qh K d st 1 2 2 K Qd st 12-3 冲击应力与变形 Q h d Q Q st

12-3冲击应力与变形 二、水平冲击 △T+△V=△U T= 3 △V=O 28 △J= 2BA-TK0A g st ■与自由落体冲击相似,理解静变形4的含义! ■公式适用于任何水平冲击线性系统(静定或超静定)
二、水平冲击 2 2 v g Q T 1 2 U P d d d st v K g T V U V 0 与自由落体冲击相似,理解静变形Δst的含义! 12-3 冲击应力与变形 Q v Q st d 1 2 2 K Qd st 公式适用于任何水平冲击线性系统(静定或超静定)

12-3冲击应力与变形 三、冲击载荷下的强度条件 ■试验表明,材料在冲击载荷作用下,其冲击强度比静强度 略高一些。 ■方便起见,建立冲击载荷作用下的光滑构件强度条件时, 仍采用静载荷时的许用应力: /max =Ka(st)max ≤[o] max =Ka(rt)max≤[z] 上述强度条件,只适用于承受冲击载荷作用的光滑构件, 对于带有缺口的构件不适用。试验表明,带有凹槽、缺口或 截面尺寸突变的构件,其承受冲击载荷的能力,远小于光滑 构件承受冲击载荷的能力,此称之为“缺口效应”。带有缺 口的构件,我们暂不研究!
三、冲击载荷下的强度条件 max max ( ) ( ) [] d d st K max max ( ) ( ) [] d d st K 试验表明,材料在冲击载荷作用下,其冲击强度比静强度 略高一些。 方便起见,建立冲击载荷作用下的光滑构件强度条件时, 仍采用静载荷时的许用应力: 上述强度条件,只适用于承受冲击载荷作用的光滑构件 , 对于带有缺口的构件不适用。试验表明,带有凹槽、缺口或 截面尺寸突变的构件,其承受冲击载荷的能力,远小于光滑 构件承受冲击载荷的能力,此称之为“缺口效应”。带有缺 口的构件,我们暂不研究! 12-3 冲击应力与变形