
佛山科学技术学院2010~2011学年第一学期 《理论力学》课程期末考试试题解答及评分标准(B) 专业、班级: 任课教师:罗冬梅 (1)M-F.×2acos30°=0 1分 Rs③M 1分 3a F-Fcos60°=0 =3M 2分 6a Fn+Fsin60°=0 F--3M 2分 6a M.+Fsin60×2a=0M,=-M2分 (2)M,()=F×a-F,×a=-15a(l-V5) 3分 F.=15KN F.=-153KN 3分 二、求A点反力(12分) RL-Fx4-0 F- (2分) F+F-9L=0F,=9g弘-E 309 (2分) 2分) F=0 (2分) MA M,+FL-S=0M,=5-F (2分) (2分 2 22 FAx FB 共4页第1页 三
佛山科学技术学院 2010~2011 学年第 一 学期 《理论力学》课程期末考试试题解答及评分标准 (B) 专业、班级: 任课教师: 罗冬梅 一. (1) − 2 cos30 = 0 o M FC a 1 分 a M FC 3 3 = 1 分 − cos60 = 0 o FAx FC a M FAX 6 3 = 2 分 + sin60 = 0 o FAy FC a M FAy 6 3 = − 2 分 M + F sin 60 2a = 0 o A C MA = −M 2 分 (2) 3 分 F y = −15 3KN 3 分 二、求 A 点反力(12 分) 0 2 − = L FC L F 2 F FC = (2 分) FAy + FC − qL = 0 2 F FAy = qL − (2 分) (2 分) FAx = 0 (2 分) 0 2 2 + − = qL M A FC L 2 2 2 qL FL M A = − (2 分) (2 分) 共 4 页第 1 页 三、 M (F)= F a − F a = −15a(1− 3) A x y F x =15KN D C F 30O FC q FB FAy FAx MA

bcP acP M,办+。M,@++cM=06分》 四、 设木箱将要滑动时拉力为F F=0 F-F=0 ∑F=0 F-G=0 F=F=G=180KN (4分) 设木箱有翻动趋势时拉力为F2 ∑M,=0 F.h-G.5=0 2 (4分) Gb E,-2h 200KN 平衡时的拉力为180KN(2分) 五、A轮,BD杆做平面运动、CD杆做瞬时平动,DE杆做定轴转动 (4分) A轮的瞬心在P1点,BC杆的瞬心在P2点 (6分) P2 B 六、V (2分) (2分) V.=V。+V.(2分) -1 (2分) 3 共4页第2页
, , 0 2 2 2 2 2 2 = + + = − + + x = y M z a b c acP M a b c bcP M (6 分) 四、 设木箱将要滑动时拉力为 F1 (4 分) 设木箱有翻动趋势时拉力为 F2 (4 分) 平衡时的拉力为 180KN (2 分) 五、 A 轮,BD 杆做平面运动、CD 杆做瞬时平动,DE 杆做定轴转动 (4 分) A 轮的瞬心在 P1点,BC 杆的瞬心在 P2点 (6 分) 六、 (2 分) (2 分) (2 分) v a v r u 3 3 = = (2 分) 共 4 页第 2 页 = = 0 0 y x F F 0 1 0 − = − = F G F F N max F max = F1 = f s G =180KN MA = 0 0 2 2 − = b F h G KN h Gb F 200 2 2 = = A B C D E P1 P2 va ve vr ae ar τ ar n aa n aa τ v a = v e + v r

a+a,=a,+a+a (2分) dcos30°+acos60°=a.c0s60°+a (2分) 5l。--t) a= (2分) -a- 6123R61 七 VA民 457 2R (4分) 汤 (1)求杆BE的角速度和角加速度, 杆OA绕轴O作定轴转动,角速度为0,故杆 OA,A端速度大小为yB=BE·0g(图3(a).杆AB作平面运动,根据速度投影法,有 [VBJAB =[YAlAB (1) 则有 VB=VA COS 300 又 VB=VA+VEA VBA=VASin30 所以 u器- (4分) yaa=vatang-√3ms AB杆的角速度为 04B='4=10 rad/s AB 3 (4分) 点D为杆BD的速度瞬心,故BD杆的角速度 0o0=A=2E-105 rad's BD0.63 (2分) 八、(10分) (1)P=mv.=imLo 1 (3分) 6 共4页第3页
(2 分) n r o e n o a t o a a a a a cos30 + cos60 = cos60 + (2 分) ) 2 3 6 1 ( 6 3 2 2 l u R u a l = − − (2 分) 七 (4 分) (4 分) (4 分) (2 分) 八、(10 分) (1) P = mv c = mL 6 1 (3 分) 共 4 页第 3 页 AB = 0 τ r n e τ a n a r a +a =a +a +a
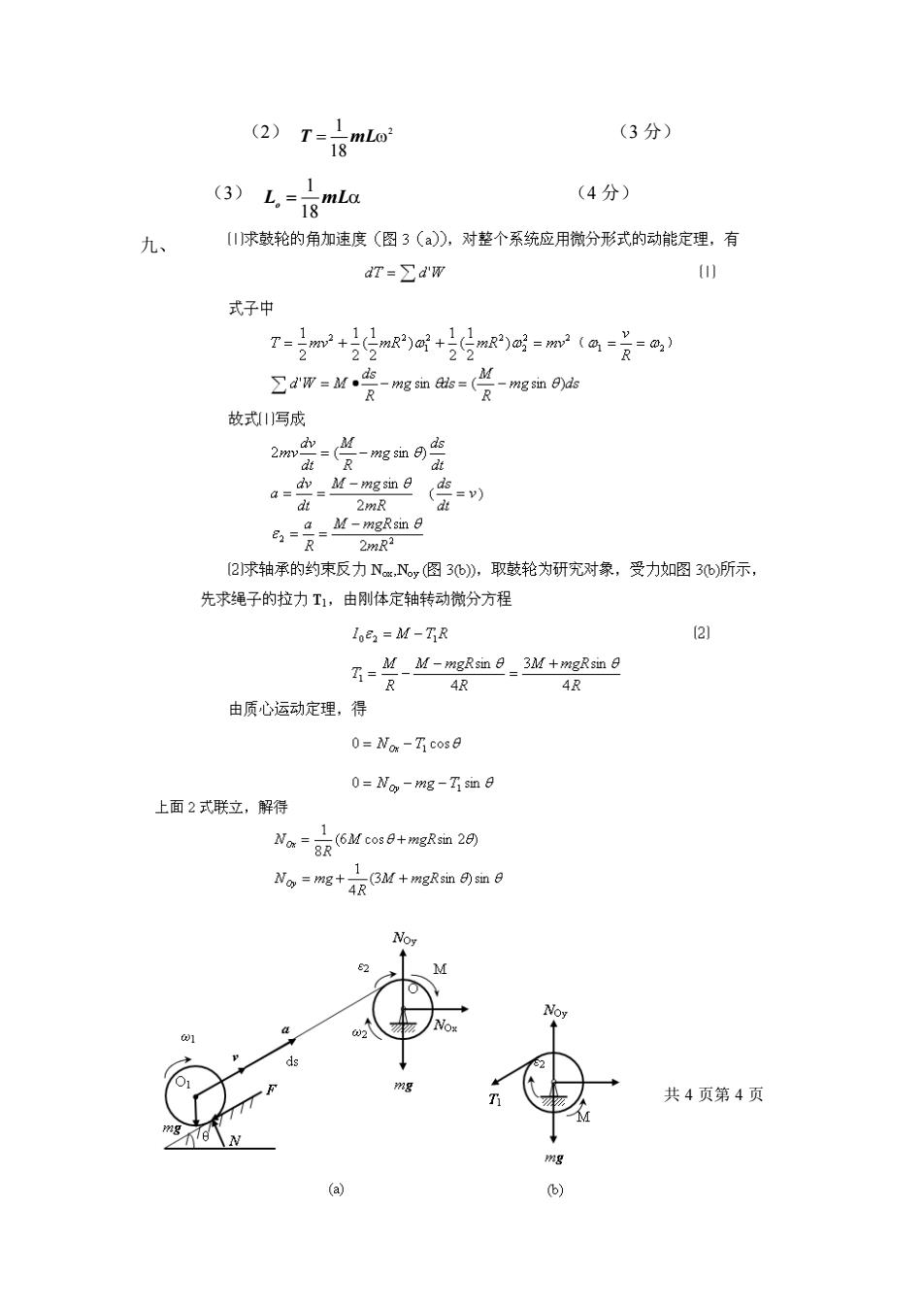
1 (2)T=三mLo (3分) 18 (3) .=8 mLa (4分) 九、 [I求鼓轮的角加速度(图3(a),对整个系统应用微分形式的动能定理,有 dT=∑d"w 1) 式子中 T=m+(mR)+(mR)m (h 2 22 22 R=@) ∑d"w=M. R -mgm=(点 -mg sin e)ds 故式)写成 2ww、M = mgn dt a=中=M-mgm0 ds d 2mR d =v) e =a=M-mgRsimn 0 = R 2mR2 [2求轴承的约束反力N,Ny(图3b),取鼓轮为研究对象,受力如图3b)所示, 先求绳子的拉力T1,由刚体定轴转动微分方程 loe2 =M-TR 2] 石=女-M-mgRa日-3M+mgR sin9 R 4R 4R 由质心运动定理,得 0=Nor -Ticose 0=No-mg-Tsim日 上面2式联立,解得 Nor= 1 (6M cos0+mgRsin 20) 8R No=mg+- BM+mgRsin)m日 4R Noy 2 M Noy No ds 共4页第4页 8 (a) (b)
(2) 2 18 1 T = mL (3 分) (3) L o = mL 18 1 (4 分) 九、 共 5 页第 4 页 共 4 页第 4 页
