佛山科学技术学院20~20学年第二学期 《理论力学》课程期末考试试题解答及评分标准(E) 专业、班级:土木工程系一 任课教师:肖莹萍 一.选择题,每题2分,共10分 1、D,2、C,3、C,4、C,5、B 二、(1) B (6分) (2)解:质心的速度v=mw 所以系统的动量为p=m=mmw(4分) 对0点的转动惯量为:J=m(2a+m2a+ma2=ma 3 对0点的动量矩为:L=邮= 3 ma'w (4分) 三、解以整体为研究对象,受力图如下: 3m F M (3分) ∑F=0,Fa+Fcos45=9×4,得F=0kN(3分) ∑F=0,F=Fsin45,得Fw=6kW(3分) ∑M,=0,M-M-q×4×号-Fsin45×3+Fcos45x4=0 3 得M=12kWm(3分) 共4页第1页
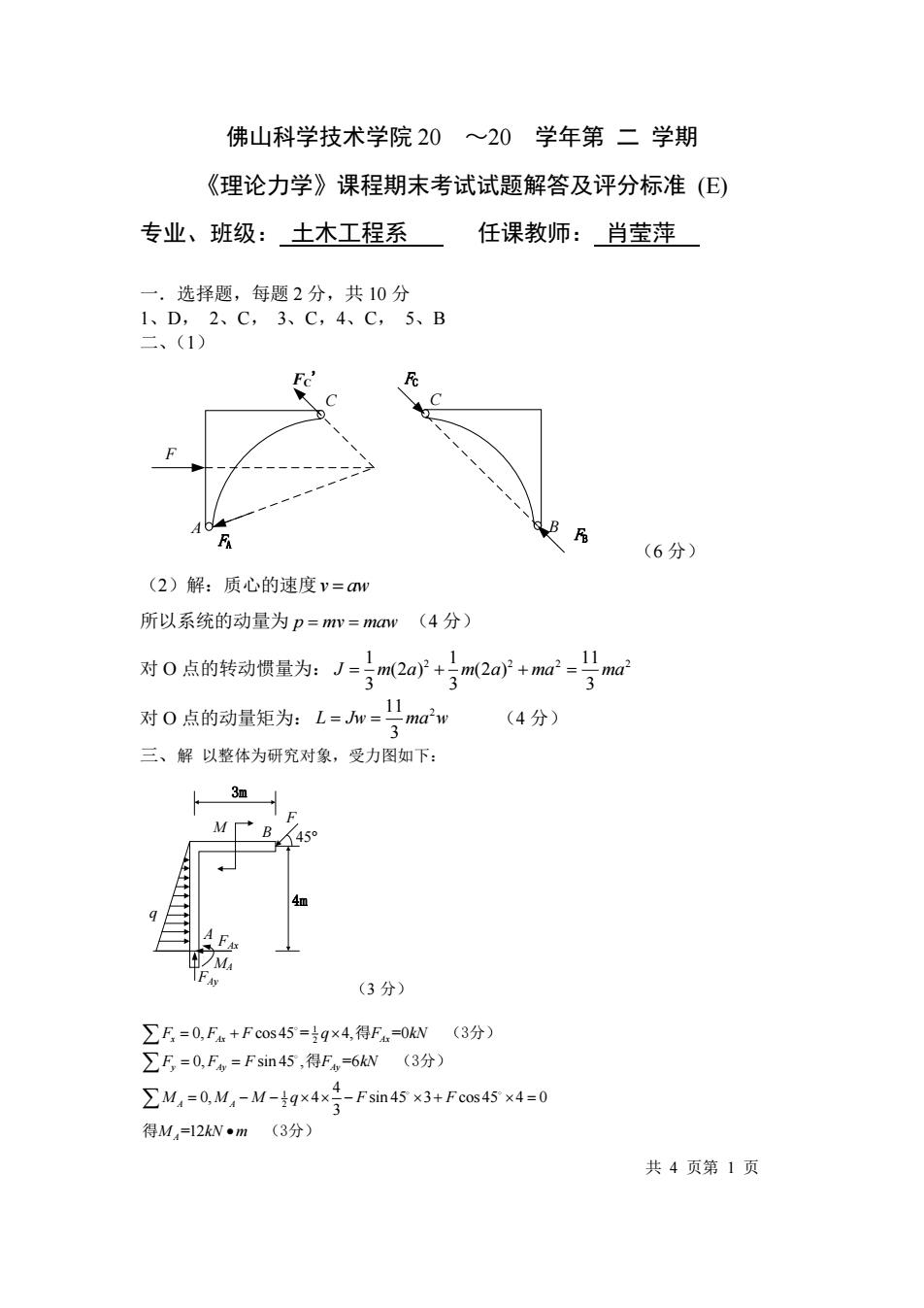
佛山科学技术学院 20 ~20 学年第 二 学期 《理论力学》课程期末考试试题解答及评分标准 (E) 专业、班级: 土木工程系 任课教师: 肖莹萍 一.选择题,每题 2 分,共 10 分 1、D, 2、C, 3、C,4、C, 5、B 二、(1) B C FB FC A C F FC' FA (6 分) (2)解:质心的速度 v aw = 所以系统的动量为 p mv maw = = (4 分) 对 O 点的转动惯量为: 1 1 11 2 2 2 2 (2 ) (2 ) 3 3 3 J m a m a ma ma = + + = 对 O 点的动量矩为: 11 2 3 L Jw ma w = = (4 分) 三、解 以整体为研究对象,受力图如下: q A M B 4m 45° F 3m FAy FAx MA (3 分) 1 2 1 2 0, cos 45 = 4, =0 0, sin 45 , =6 4 0, 4 sin 45 3 cos 45 4 0 3 =12 x Ax Ax y Ay Ay A A A F F F q F kN F F F F kN M M M q F F M kN m = + = = = − − − + = • 得 (3分) 得 (3分) 得 (3分) 共 4 页第 1 页

四、解: G G 30 G (4分) 取物块A为研究对象。 (1)设物体A达到沿斜面下滑的临界状态,如图5.11(b)所示。 ∑Fx=0G2cos30°-Gsin20°+F,=0 (2分) 2F,=0G2sin30°-Gcos20°+FN=0(2分) F,=fFN (1分) 解得 G2=sin20°-fcos20 cos30-,sim30-G-40.2kN ( )设物体A达到绕点B翻倒的临界状态[图5.11(d)门。 ∑M=0 Gcos30×a-Gsim20x9-Gcos20×2-0 (2分) 得 G,-lcos20+hsn20×9-104.2kN acos30 2 (2分) 五、 5=5F=0=-5 (1.5分) 2 i j M(E)= 0b b =-6Fh+ FbK (3分) 2 2 F0 6 2 21 F2=-F Fy=F F2=-2F (1.5分) k M(E)= b 02b =-2Fbi+0j+Fbk (3分) -F F-2F 5=5-F5=FE=( -2)F (1.5分) MP)=-S-2肠M,r)-5BM0)=-5+5 (1.5分) 2 共4页第2页
四、解: (2分) (2分) (1分) (1分) (2分) (2分) (4分) 五、 1 1 1 0 1 2 2 2 0 2 6 6 0 2 2 666 ( ) 0 222 6 6 0 2 2 2 ( ) 0 2 2 0 2 6 ( 1) 2 x y z x y z x y F F F F F i j k M F b b Fbi Fbj Fbk F F F F F F F F i j k M F b b Fbi j Fbk F F F F F F F F = = = − = = − + − − = − = = − = = − + + − − = − = (1.5分) (3分) (1.5分) (3分) 6 ( 2) 2 6 6 6 ( ) ( 2) ( ) ( ) ( 1) 2 2 2 z x y z F M F Fb M F Fb M F Fb = − − = − − = = − + (1.5分) (1.5分) 共 4 页第 2 页

六 (2分) 首先计算连杆AB的角速度。由题意得A点逸度的大小为 %=OA·w=w (2分) 其方向如因 因DB杆饶D轴转动,而B点是三杆的较接点,固此由转动杆件BD的运动可加垂直 于DB。根据瞬心确定方法可得C:点即是AB杆的速度瓣心,于是 连杆AB的角速度为 w一品B品清2 (2分) 转向由%的指向确定,如图9.26所示。由此可得B,点的速度大小为 m=GB·uw=ABco60×2w-号e (2分) 来次来解连杆BC的商建度。用滑块语参直方向运动,故此的方向也浴香直方有, 可确定C为BC杆的醉心。连杆BC的角速度为 wx一C&是 通过几何关系可以看出CB=C,C=BC=l,于是可得 m瓷- (2分) 其为逆时针转向。 (2分) 其指向垂直向下。 七、解: (3分) 画出动点的速度合成失量图 其中三个速度的方向均为已知,且绝对速 度的大小为=OA·u=125.6cm/s,由几何关系可求得 ,=,==125.6cm/s (3分) 则滑道BCD的连度vm=125.6cm/s。 画出动点的加速度合成夫量图,如图8.12所示。由加速度合成定理有 a;+a'=a,+a+a; (3分) 302 20 头中,a=0,心G=Rd,a=品而a,和为未知量,假设关指向如图所示,建立加困所 示的投形坐标轴,将各失量投影到刀袖上,得 -acos60°=-a.cos30°+af (3分) 解得 a.-gea60+g=2740cm/s=27.4mh c08300 (2分) a,即为清道BCD的加追度,结果为正:表明所假设a的指向与实际指向一致。 共4页第3页
六 (2分) (2分) (2分) (2分) (2分) (2分) (2分) 七、解: (3分) (3分) (2分) (3分) (3分) 共 4 页第 3 页

八、解:A、B两物块作直线运动,取坐标系Oxy,则A、B两物块的运动微分方程为: m心4=mg-F sin0 (1)(2分) m成a=Fa'cos0 (2)(2分) 由几何关系可知 y=Isin0 (3)(1分) x8=Icos0 (4)(1分) 将上式对时间求导,得 少a4=l0cos0 =10 cos0-10-sin0 (5)(2分) g=-10sin0 g=-16sin0-102cos0 (6)(2分) 把(5)和(6)分别代入(1)和(2) 整理得: F-mg tan0+ml(tan1) (1分) tan-1 初始时刻4、物块速度为0,故0-0,代入上式得F6Bm 2 (1分) 共4页第4页
八、解:A、B 两物块作直线运动,取坐标系 Oxy,则 A、B 两物块的运动微分方程为: θ A B O x y sin cos sin cos cos cos A AB B AB A B A A my mg F mx F y l x l y l y l l = − = = = = = − (1) (2分) (2) (2分) 由几何关系可知 (3) (1分) (4) (1分) 将上式对时间求导,得 2 2 2 2 2 sin sin sin cos tan (tan 1) = tan 1 3 =0, = 2 B B AB AB x l x l l mg ml F mg A B F = − = − − + + − (5) (2分) (6) (2分) 把(5)和(6)分别代入(1)和(2) 整理得: (1分) 初始时刻 、 物块速度为0,故 代入上式得 (1分) 共 4 页第 4 页