
1.3解0如题1.3.2图 ↑y a c a B 第1.3题图 y 、a 人0 B 1 题1.3.2图 由题分析可知,点C的坐标为 x=rcoso+acosy y=asinv 又由于在△A0B中,有”=2a (正弦定理)所以 sin y sin sin 2asin y2y r 联立以上各式运用 sin2 +cos2=1 由此可得 coso=x-acosy_x-va2-y2 得 4y2x2+a2-y2-2xVa2-y2 得 3y2+x2+a2-r2=2xNa2-y7 化简整理可得
1.3 解 (1) 如题 1.3.2 图 x y C a B A r O a 第1.3题图• • A B r C a x yO 题1.3.2图 由题分析可知,点 C 的坐标为 = = + sin cos cos y a x r a 又由于在 AOB 中,有 sin 2 sin r a = (正弦定理)所以 r y r 2asin 2 sin = = 联立以上各式运用 sin cos 1 2 2 + = 由此可得 r x a y r x a 2 2 cos cos − − = − = 得 1 4 2 2 2 2 2 2 2 2 2 = + − − − + r x a y x a y r y 得 2 2 2 2 2 2 3y + x + a − r = 2x a − y 化简整理可得
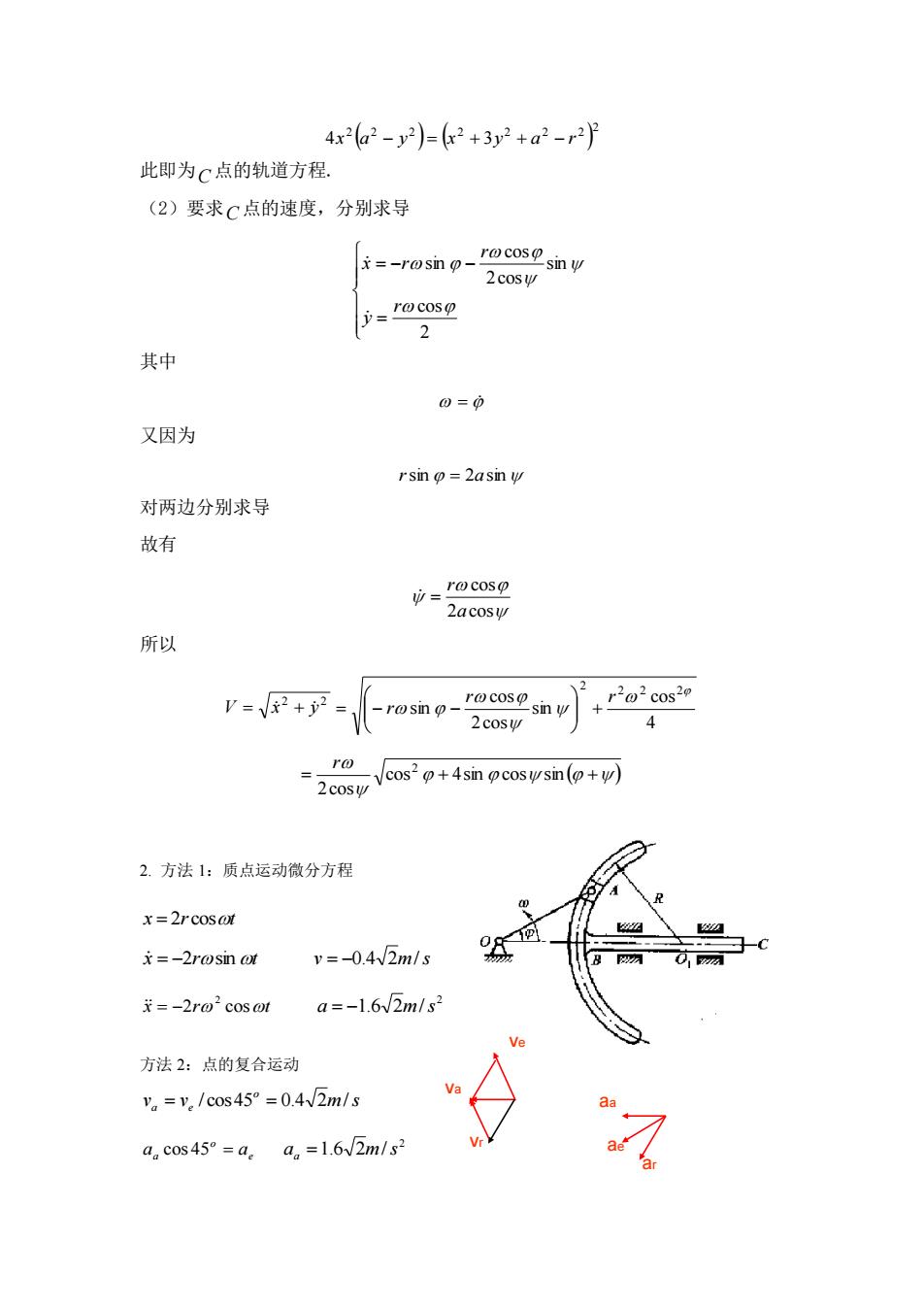
4x2a2-y2)=(2+3y2+a2-r2)月 此即为C点的轨道方程. (2)要求C点的速度,分别求导 x=-rosin rocoso sin w 2cosy rocosp y= 2 其中 0=0 又因为 rsin =2asin w 对两边分别求导 故有 ro coso 中= 2acosy 所以 V=2+2 ro cos r2@2cos20 rosmn o- sin u 2cosy 4 "0 cos-p+4sin ocosusin (+y) 2cosy 2.方法1:质点运动微分方程 x=2rcosot =-2rosin ot v=-0.4V2m/s =-2ro-cosot a=-1.6V2m/s2 Ve 方法2:点的复合运动 v。=v。/cos45°=0.4V2m/s Va aa a.cos45°=a。an=1.6W2m/s2 ae
( ) ( ) 2 2 2 2 2 2 2 2 4x a − y = x + 3y + a − r 此即为 C 点的轨道方程. (2)要求 C 点的速度,分别求导 = = − − 2 cos sin 2cos cos sin r y r x r 其中 = 又因为 rsin = 2asin 对两边分别求导 故有 2 cos cos a r = 所以 2 2 V = x + y 4 cos sin 2cos cos sin 2 2 2 2 r r r + = − − ( ) = cos + 4sin cos sin + 2cos r 2 2. 方法 1:质点运动微分方程 x = 2r cost x = −2rsint v = −0.4 2m/s x 2r cost 2 = − 2 a = −1.6 2m/s 方法 2:点的复合运动 v v m s o a e = / cos45 = 0.4 2 / e o aa cos 45 = a 2 a 1.6 2m/s a = va ve vr aa ae ar

解: a'=asin60°=r8 a"=ac0s60°=ro2 两式相除: 860°= d 02 2.0=3o2 d 6=V3o2 do =3dp do=3o o do.dp=√3o dt do 0=0,ev3o do dt =@e3o edo adt eh-ml+C 、 1 p=万h1-5a, 解:动点M,动系OD杆 t=1s时,中=30° D OM=108 0= 2π2 3 C Va=V。+V y=0M0=0C.9=3x2 coso y,==23m2y=y,sn0=V3x2 cos
3 0 e dt d = e d dt 0 3 = − − e = t + C − 0 3 3 3 t 1 3 0 1 ln 3 1 − = a φ O = a = r a sin 60 τ n 2 a = acos60 = r 两式相除: 2 60 = tg 2 = 3 2 3 = dt d 2 3 = d d dt d 2 3 = d d d d = 3 = 0 3 0 d d 3 0 = e φ A B C O D M 解:动点M,动系OD杆 ve va vr 2 3 cos = = = ve OM OC 2 2 3 cos = = e a v v 2 vr = va sin = 3 t =1s 时,φ=300 2 36 3 3 108 OM = = v a =v e +v r vr va ve 解:

解:动点:C(CD上),动系:OAB 绝对运动:铅直线运动: 相对运动:斜直线运动: 牵连运动:转动 0a=0。+0 D。=,830°=0Co1g30=y cos30°o830= rω 3 +a=+a0@+ 中 X a,c0s30°=-ac0s30°+0+ak =10N3rw2 aa = 注意!不要掉了ak 9 VA D 解: AB作平面运动,用速度投影 定理求VB VBC0S30°=y4=ro C为轮B的瞬心,有: VB ROBC 请思考:当中=90时vo= VD =2R@BC =2VB =4v3 r0 3
C B A O D ω φ ve 解: 动点:C(CD上), 动系:OAB 绝对运动: 铅直线运动; 相对运动: 斜直线运动; 牵连运动: 转动 υ a =υ e +υ r va vr tg30 cos30 r υa = ve tg30 = OCωtg30 = rω 3 2 = k τ r τ n e τ n a n a a a a a a a a e r + = + + + + ar ae ak ? ? k n aa cos30 a cos30 0 a e = − + + 2 a 3 rω 9 10 a = 注意!不要掉了ak ω O A B D φ R r 解: vA vB C ωBC vB = vA = r cos30 C为轮B的瞬心,有: AB作平面运动,用速度投影 定理求VB: B R BC v = vD D BC B v = 2R = 2v r 3 4 3 = 请思考:当φ=900时vD=?