
授课内容(四) 复习平面汇交力系 §2-2平面力对点之矩的概念及计算 §2-3平面力偶与平面力偶系 2018.3.15
授课内容(四) §2-2 平面力对点之矩的概念及计算 §2-3 平面力偶与平面力偶系 复习平面汇交力系 2018.3.15

例2-3已知: 活塞杆压力=3kN,=1500mm,h=200mm.忽略自重; 求:平衡时,压块C对工件与地面的压力,AB杆 受力
例2-3 已知: 活塞杆压力=3kN, l=1500mm, h=200mm.忽略自重; 求:平衡时,压块C对工件与地面的压力,AB杆 受力。 D E A B C l l h
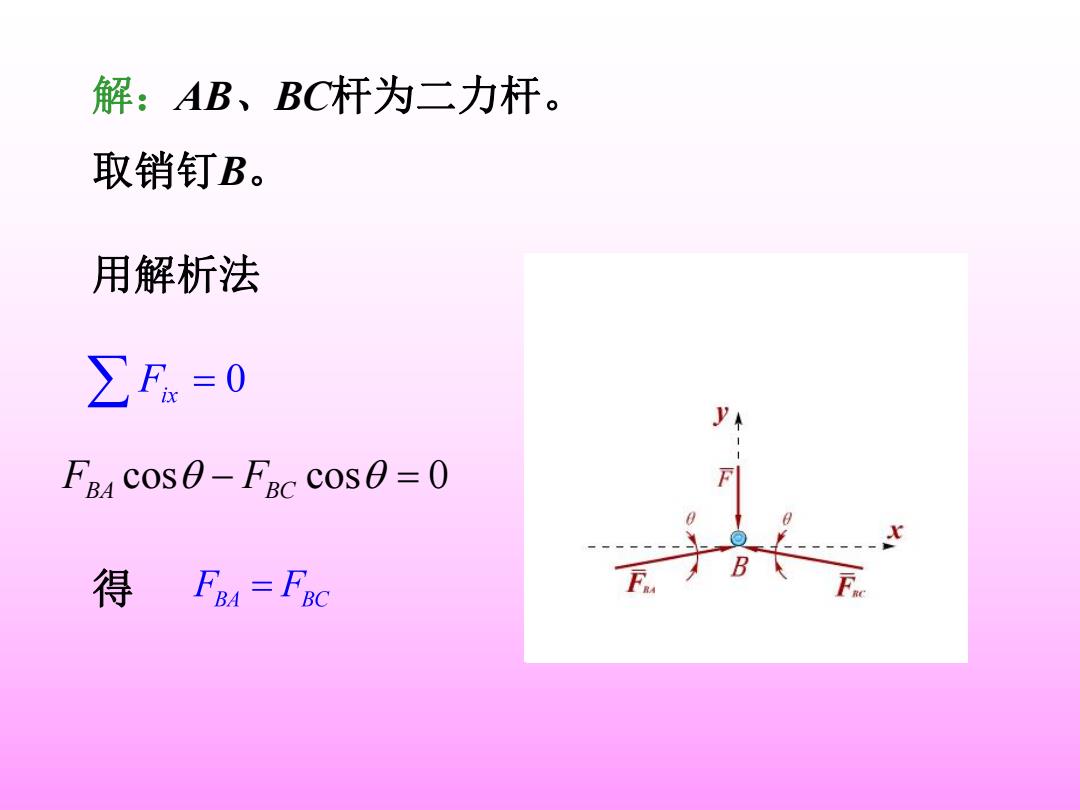
解:AB、BC杆为二力杆。 取销钉B。 用解析法 ∑F=0 y FBA cos0-FBc cos=0 得FBA=FaC
解:AB、BC杆为二力杆。 取销钉B。 用解析法 得 FBA cos FBC cos 0

∑F=0 FBa sin0+FBc sin0-F=0 解得 FBA=FBC =11.35kN 选压块C ∑F=0 FCB COS0-F=0 解得R.5o0=分1125N 2h ∑F=0 -F cB sin e+Fcy=0 解得 FCy =1.5kN
解得 选压块C 解得 解得

解静力学平衡问题的一般方法和步骤 1.选择研究对象 与已知力(或已求出的力)、未知力有直接关系, 便于应用平衡条件由已知条件求未知力; 2.画受力图 根据研究对象所受外部载荷、约束及其性质, 对研究对象进行受力分析并得出它的受力图。 3.建立坐标系 最好选取有一轴与一个未知力垂直。 4.列平衡方程解出未知量 要注意各力投影的正负号 如果计算结果中出现负号时,说明原假设方向与实际受力方向相反
1.选择研究对象 与已知力(或已求出的力)、未知力有直接关系, 便于应用平衡条件由已知条件求未知力; 2.画受力图 根据研究对象所受外部载荷、约束及其性质, 对研究对象进行受力分析并得出它的受力图。 3.建立坐标系 最好选取有一轴与一个未知力垂直。 4.列平衡方程解出未知量 要注意各力投影的正负号 如果计算结果中出现负号时,说明原假设方向与实际受力方向相反 解静力学平衡问题的一般方法和步骤
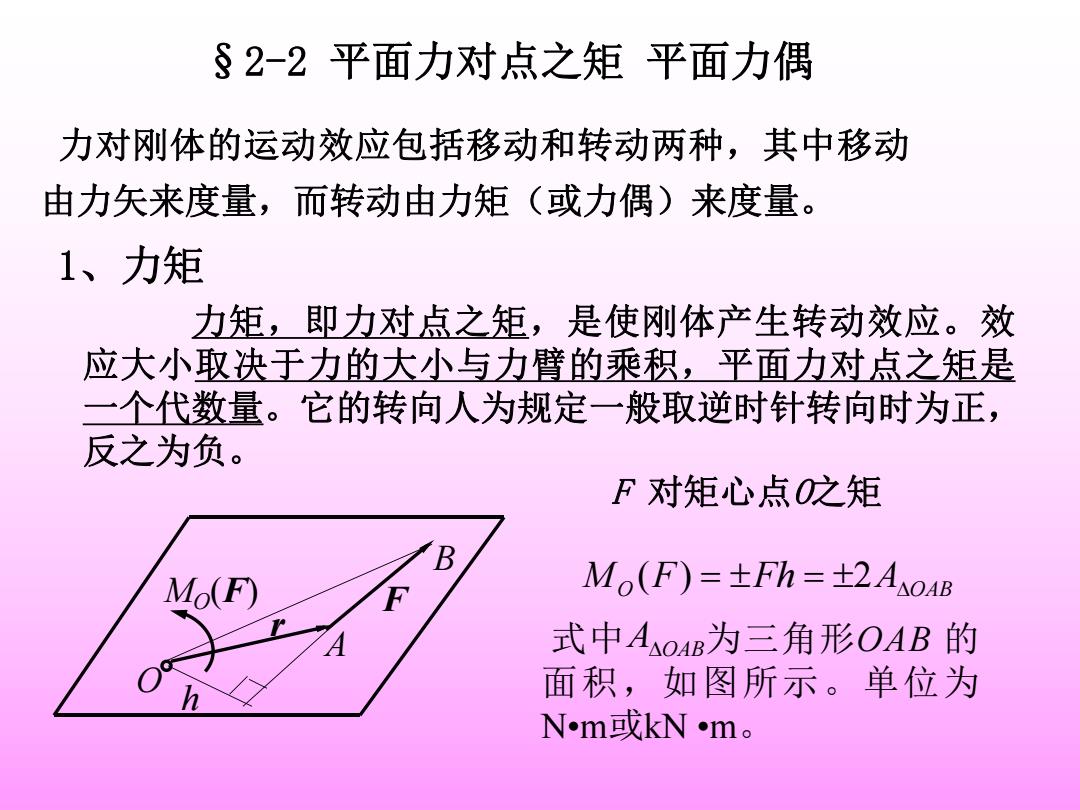
§2-2平面力对点之矩平面力偶 力对刚体的运动效应包括移动和转动两种,其中移动 由力矢来度量,而转动由力矩(或力偶)来度量。 1、力矩 力矩,即力对点之矩,是使刚体产生转动效应。效 应大小取决于力的大小与力臂的乘积,平面力对点之矩是 一个代数量。它的转向人为规定一般取逆时针转向时为正, 反之为负。 F对矩心点之矩 Mo(F) Mo(F)=±Fh=+2AoAB 式中AoAB为三角形OAB的 面积,如图所示。单位为 Nm或kNm
§2-2 平面力对点之矩 平面力偶 力对刚体的运动效应包括移动和转动两种,其中移动 由力矢来度量,而转动由力矩(或力偶)来度量。 力矩,即力对点之矩,是使刚体产生转动效应。效 应大小取决于力的大小与力臂的乘积,平面力对点之矩是 一个代数量。它的转向人为规定一般取逆时针转向时为正, 反之为负。 F 对矩心点O之矩 O F A OAB M F h ( ) 2 1、力矩 O h r F A MO(F) B 式中 为三角形OAB 的 面积,如图所示。单位为 N•m或kN •m。 AOAB
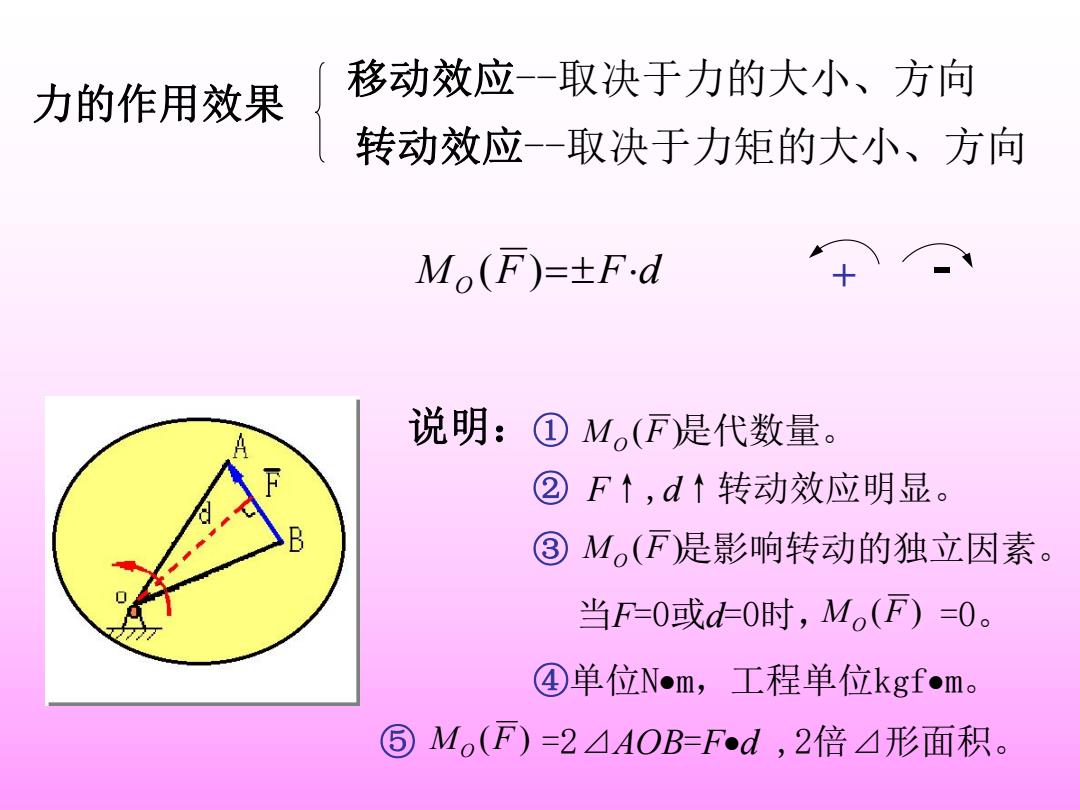
移动效应--取决于力的大小、方向 力的作用效果 转动效应-取决于力矩的大小、方向 Mo(F)=±Fd 说明:①M(F是代数量。 ②F↑,d↑转动效应明显。 ③ M。(F是影响转动的独立因素。 当F=0或d0时,Mo(F)=0。 ④单位N●m,工程单位kgfm。 ⑤1 Mo(F)=2AOB=Fd,2倍△形面积
① MO (F )是代数量。 当F=0或d=0时,MO (F ) =0。 ③ MO (F )是影响转动的独立因素。 ⑤ MO (F ) =2⊿AOB=Fd ,2倍⊿形面积。 移动效应--取决于力的大小、方向 M F F d + - O ( ) 说明: ② F↑,d↑转动效应明显。 ④单位Nm,工程单位kgfm。 转动效应--取决于力矩的大小、方向 力的作用效果
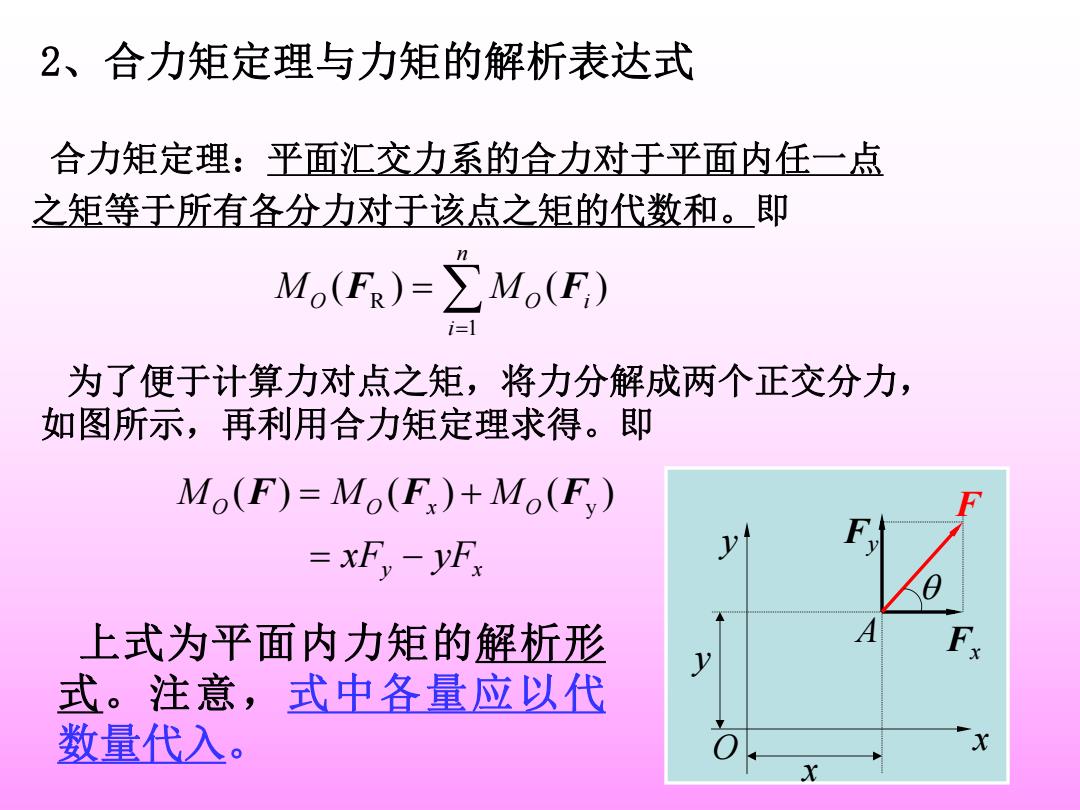
2、合力矩定理与力矩的解析表达式 合力矩定理:平面汇交力系的合力对于平面内任一点 之矩等于所有各分力对于该点之矩的代数和。即 Mo(FR)=∑Mo(F) i=l 为了便于计算力对点之矩,将力分解成两个正交分力, 如图所示,再利用合力矩定理求得。即 Mo(F)=Mo(F)+Mo(Fy) =xFy-yF 上式为平面内力矩的解析形 式。注意,式中各量应以代 数量代入。 X X
2、合力矩定理与力矩的解析表达式 合力矩定理:平面汇交力系的合力对于平面内任一点 之矩等于所有各分力对于该点之矩的代数和。即 ( ) ( ) 1 R i n i MO F MO F 为了便于计算力对点之矩,将力分解成两个正交分力, 如图所示,再利用合力矩定理求得。即 y x O O x O xF yF M M M ( ) ( ) ( ) F F Fy 上式为平面内力矩的解析形 式。注意,式中各量应以代 数量代入。 O y x A y x Fy Fx F

合力F对点O之矩的解析表达式为 MoEa)-∑(ya = 如图所示,如果已知:F、0、p、1,求力F对点0位矩 (1)按力矩的定义 Mo(F)=F.h=FIsin90-0+p)=Flcos-) (2)应用合力矩定理 Mo(F)=Mo(E)+Mo(F) =Fsine.Isin+Fcos0.lcosp+ =FIcos-p)
合力FR对点O之矩的解析表达式为 如图所示,如果已知:F 、、 、l,求力F 对点O之矩 M ( ) Fh Flsin(90 ) Flcos( ) O F (1)按力矩的定义 (2)应用合力矩定理 cos( ) sin sin cos cos ( ) ( ) ( ) Fl F l F l MO F MO Fx MO Fy

已知: a,b,F,a 求: M()=? 解:户=户+F 由合力矩定理 M()=M厅)+M.(厅,) Fcosa =-Fxb+Fya Fy =Fsina --Fbcosa+Fasina =F(asina-bcosa)
o a b F 已知: a, b, F, 求: 解: M F ? o 由合力矩定理 Mo F Mo Fx Mo Fy F Fx Fy Fx Fcos Fy Fsin F b F a x y Fbcos Fasin Fasin bcos