
第7章1 刚体的简单运动 §7-1刚体的平行移动 §7-2刚体绕定轴的转动 §7-3转动刚体内各点的速度和加速度 2018.4.26
第7章 刚体的简单运动 §7-1 刚体的平行移动 §7-2 刚体绕定轴的转动 §7-3 转动刚体内各点的速度和加速度 2018.4.26
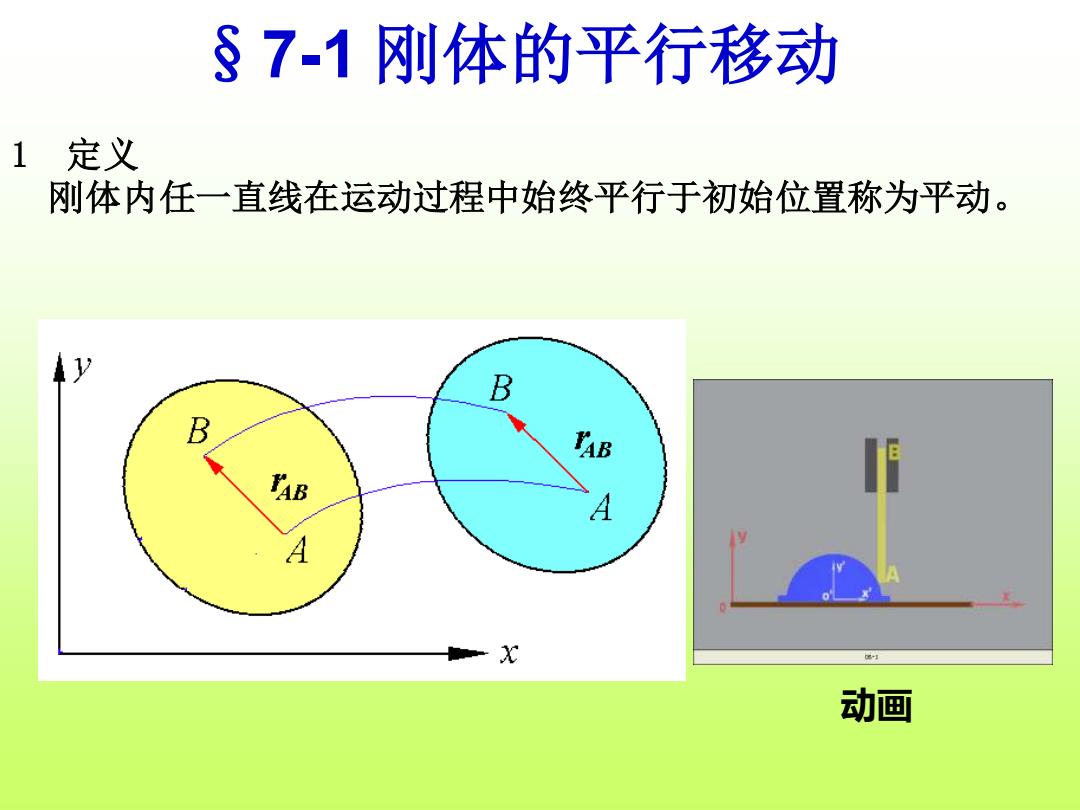
§7-1刚体的平行移动 1定义 刚体内任一直线在运动过程中始终平行于初始位置称为平动。 1 B B A A 动画
1 定义 刚体内任一直线在运动过程中始终平行于初始位置称为平动。 §7-1 刚体的平行移动 动画
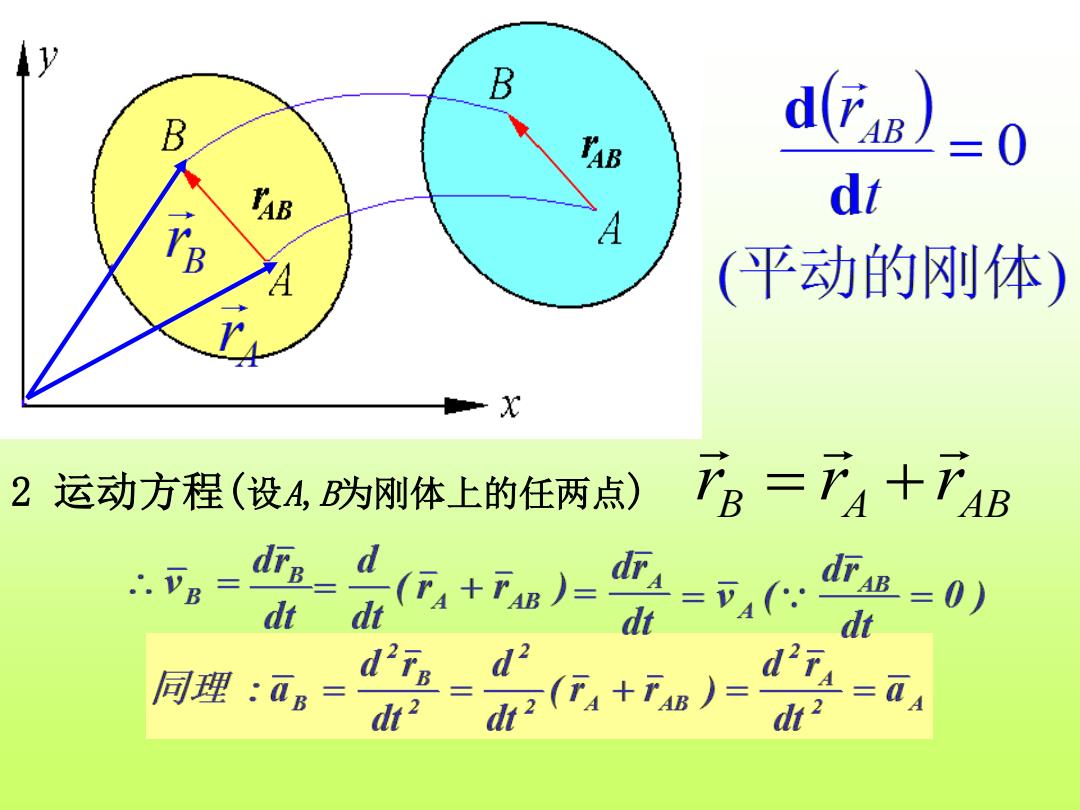
y B B TAB d(a)=0 di B A (平动的刚体) 2运动方程(设A,为刚体上的任两点) B=下4十下4B dt ,+a==可, dt dt 面B=0) dt 同理:ū8= (+w)= 万A=aA dt2
2 运动方程(设A,B为刚体上的任两点) B A AB r r r = +
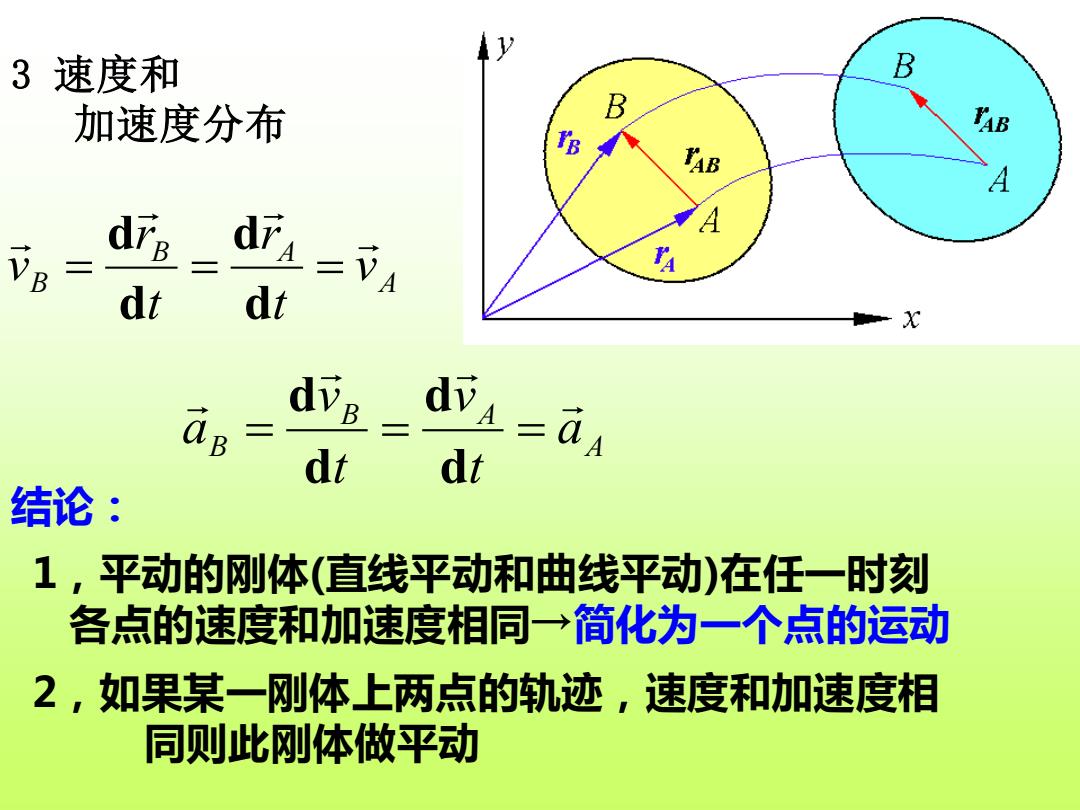
3速度和 B 加速度分布 B TAB B TAB A A VB d d 二VA dt di ag= d城4=aA dt dt 结论: 1,平动的刚体(直线平动和曲线平动)在任一时刻 各点的速度和加速度相同一→简化为一个点的运动 2,如果某一刚体上两点的轨迹,速度和加速度相 同则此刚体做平动
2,如果某一刚体上两点的轨迹,速度和加速度相 同则此刚体做平动 3 速度和 加速度分布 A B A B v t r t r v = = = d d d d A B A B a t v t v a = = = d d d d 结论: 1,平动的刚体(直线平动和曲线平动)在任一时刻 各点的速度和加速度相同→简化为一个点的运动

口平移的特点 口刚体上的各点具有形状相同的运动轨迹 刚体上的各点在某一瞬时具有相同的速度 和加速度: 刚体平移时的运动分析可以简化为其上任 意一点(一般取为质心的运动分析;
平移的特点 刚体上的各点具有形状相同的运动轨迹; 刚体上的各点在某一瞬时具有相同的速度 和加速度; 刚体平移时的运动分析可以简化为其上任 意一点(一般取为质心)的运动分析;
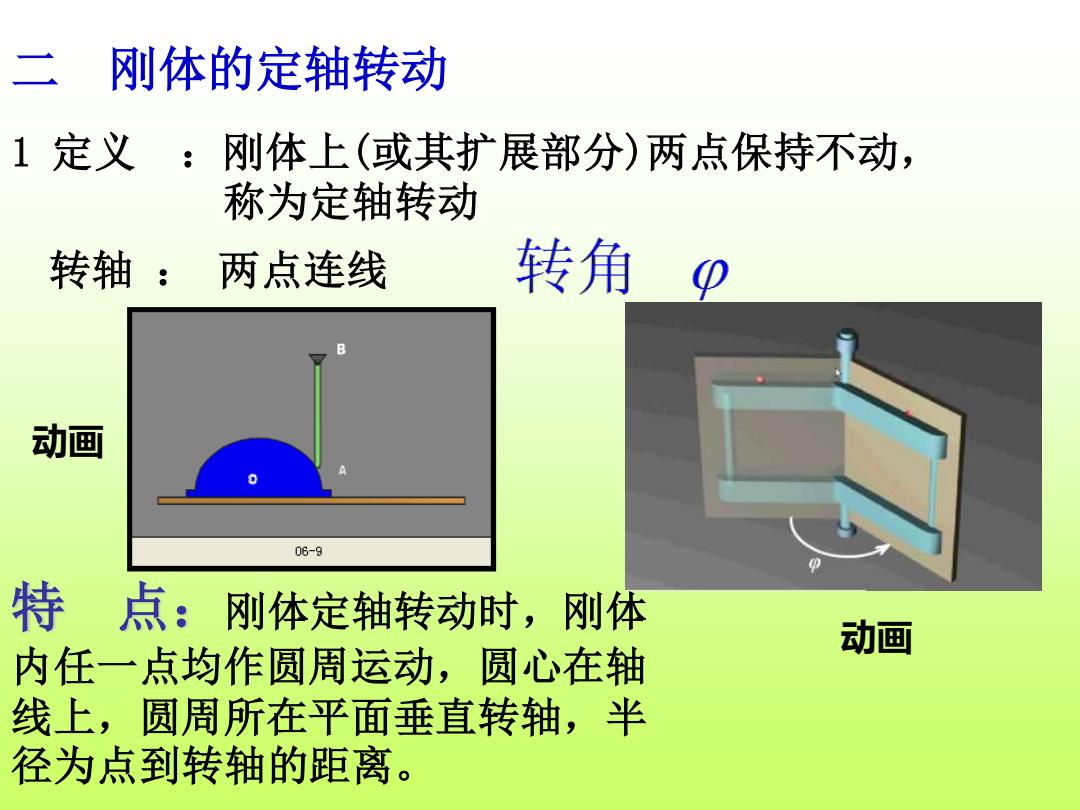
二 刚体的定轴转动 1定义 :刚体上(或其扩展部分)两点保持不动, 称为定轴转动 转轴:两点连线 转角0 动画 06-9 特点: 刚体定轴转动时,刚体 动画 内任一点均作圆周运动,圆心在轴 线上,圆周所在平面垂直转轴,半 径为点到转轴的距离
1 定义 :刚体上(或其扩展部分)两点保持不动, 称为定轴转动 转轴 : 两点连线 二 刚体的定轴转动 特 点:刚体定轴转动时,刚体 内任一点均作圆周运动,圆心在轴 线上,圆周所在平面垂直转轴,半 径为点到转轴的距离。 动画 动画
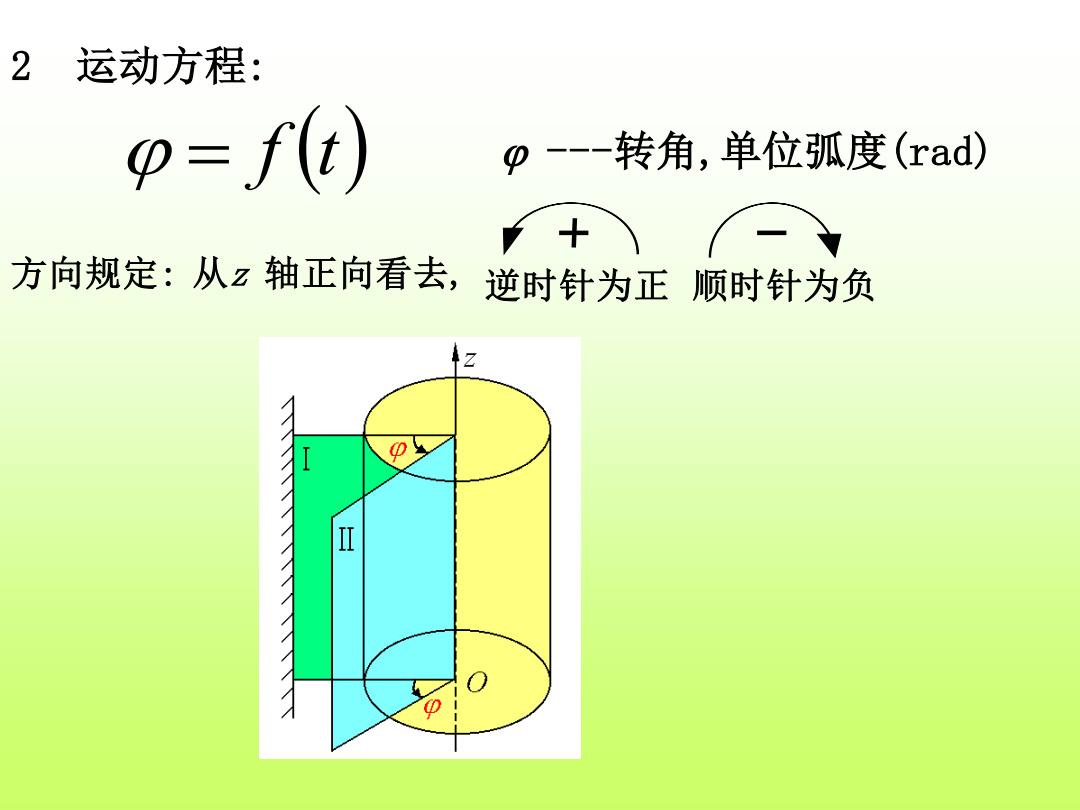
2运动方程: p=f(t) p--转角,单位弧度(rad) 十 方向规定:从z轴正向看去, 逆时针为正顺时针为负 0 I
2 运动方程: = f (t) ---转角,单位弧度(rad) 方向规定: 从z 轴正向看去, 逆时针为正 顺时针为负
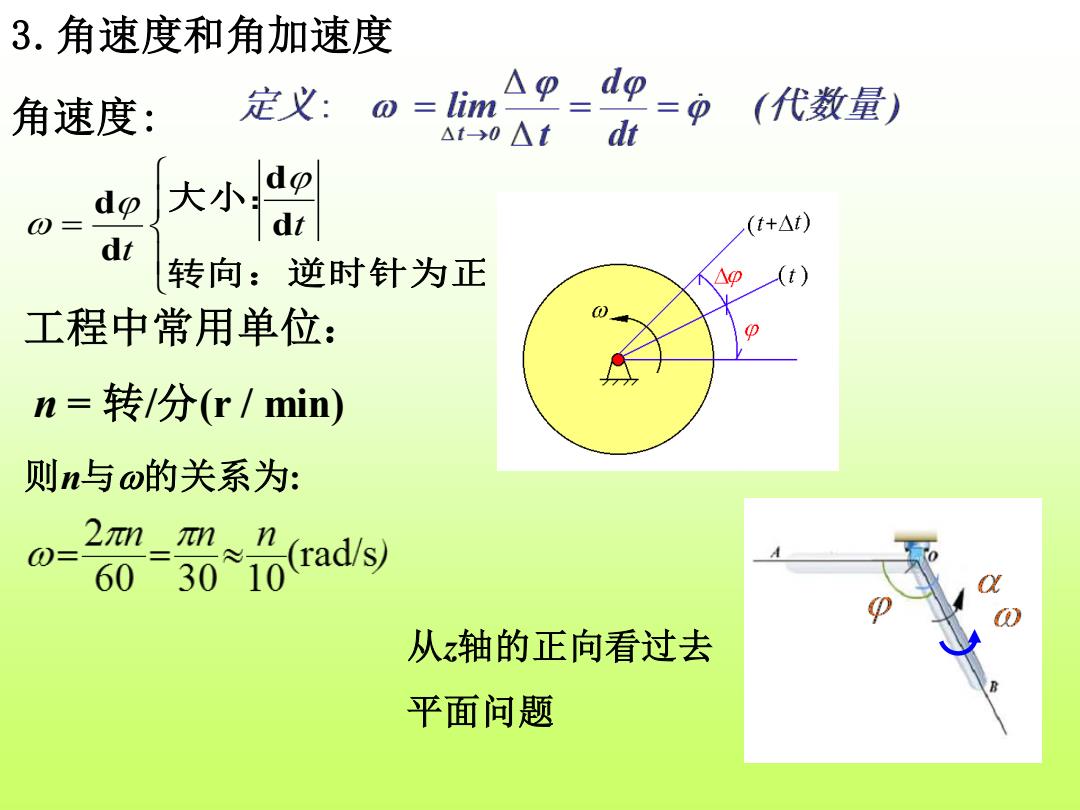
3.角速度和角加速度 △9 角速度: 定义:o=lim ,(代数量) △t-→0 △t _dt dp 大小 dp 0= (t+△t) dt 转向:逆时针为正 △p (t) 工程中常用单位: n=转/分r/min) 则n与o的关系为: 20-0*6ad时 从z轴的正向看过去 平面问题
3.角速度和角加速度 = 向:逆时针为正 大 小 转 : t t d d d d 从z轴的正向看过去 平面问题 角速度: 工程中常用单位: n = 转/分(r / min) 则n与的关系为:

2、角加速度: △0 do .∴角加速度:&=1im 4t→0 At dt e-9-1(D 单位:rad/s2(代数量) 与o方向一致为加速转动,与o方向相反为减速转动 3、当角加速度为常量时,匀变速转动: 0=⊙o+Bt =%+0a1+2会
2、角加速度: 与方向一致为加速转动, 与 方向相反为减速转动 单位:rad/s2 (代数量) 2 0 0 0 2 1 t t t = + + = + 3、当角加速度为常量时,匀变速转动:
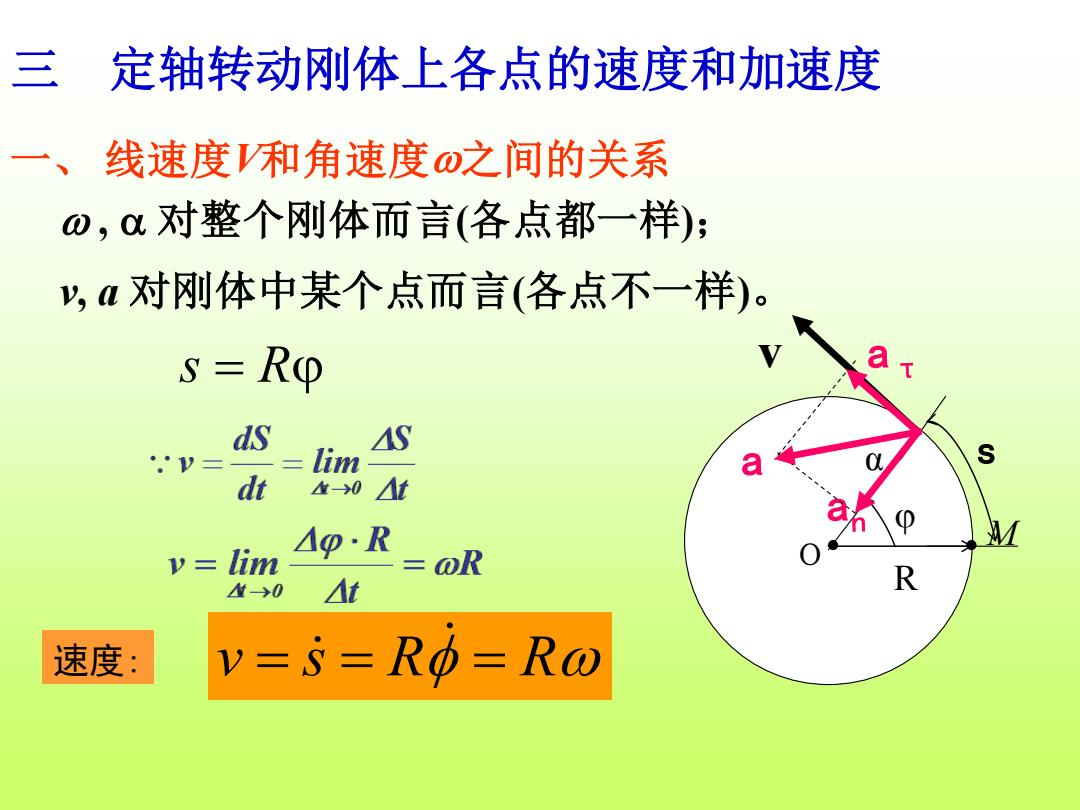
三定轴转动刚体上各点的速度和加速度 线速度和角速度o之间的关系 o,对整个刚体而言(各点都一样); y,a对刚体中某个点而言(各点不一样)。 s Ro ds AS lim dt 0 △t lim p·R @R -→0 t 速度: v=s=Ro=R@
, 对整个刚体而言(各点都一样); v, a 对刚体中某个点而言(各点不一样)。 一、 线速度V和角速度之间的关系 s M v o R α s = R 速度: v = s = R = R 三 定轴转动刚体上各点的速度和加速度