
第13章质点系动能定理 ▣ 动能定理与机械能守恒 日 动力学普遍定理的综合应用 日 讨论
□ 动能定理与机械能守恒 □ 讨论 第13章 质点系动能定理 □ 动力学普遍定理的综合应用
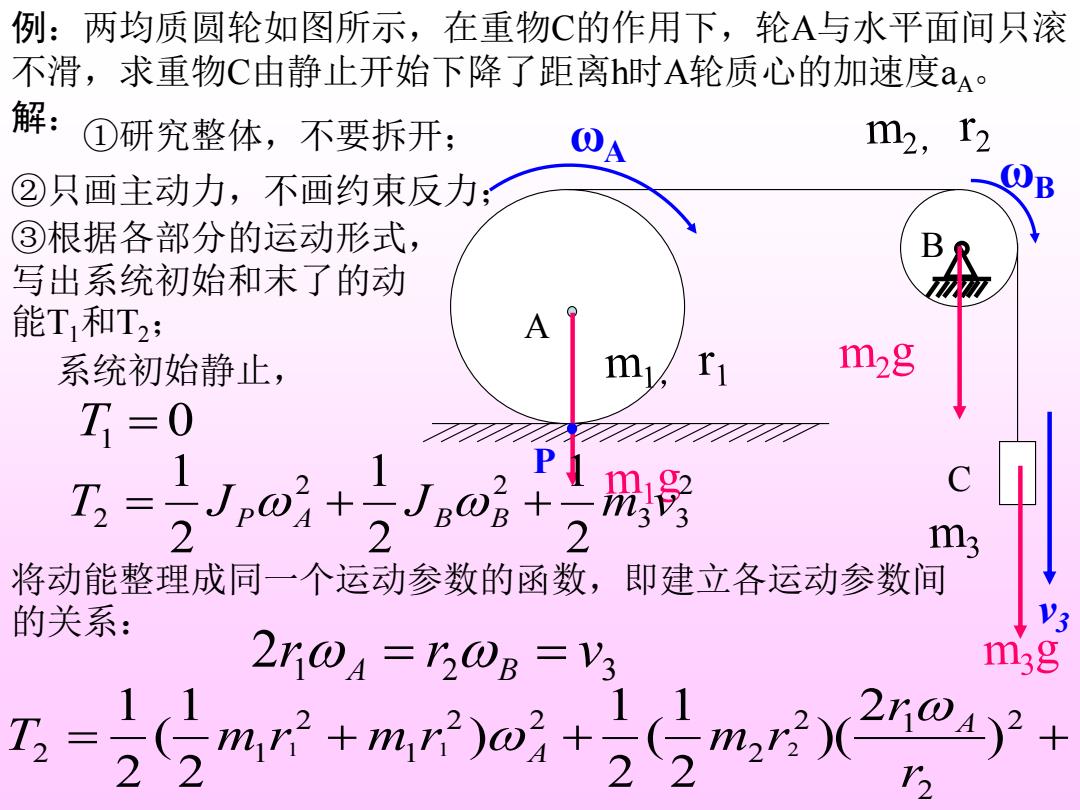
例:两均质圆轮如图所示,在重物C的作用下,轮A与水平面间只滚 不滑,求重物C由静止开始下降了距离h时A轮质心的加速度aA。 解: ①研究整体,不要拆开; m2 ②只画主动力,不画约束反力: ③根据各部分的运动形式, 写出系统初始和末了的动 能T,和T2: A 系统初始静止, m ri m2g T=0 -1,wi+1 m; 将动能整理成同一个运动参数的函数,即建立各运动参数间 的关系: 2r@=r0B =V3 m3g 11 D= 2兮m+m0+25m,20
例:两均质圆轮如图所示,在重物C的作用下,轮A与水平面间只滚 不滑,求重物C由静止开始下降了距离h时A轮质心的加速度aA。 C A B 解:①研究整体,不要拆开; ②只画主动力,不画约束反力; ③根据各部分的运动形式, 写出系统初始和末了的动 能T1和T2; T1 = 0 系统初始静止, 2 3 3 2 2 2 2 1 2 1 2 1 T J J m v = P A + B B + P ωA ωB v3 将动能整理成同一个运动参数的函数,即建立各运动参数间 的关系: 2 1 2 3 r r v A = B = = + + + 2 2 2 1 2 2 2 1 2 2 1 ) 2 )( 2 1 ( 2 1 ) 2 1 ( 2 1 1 1 2 r r T m r m r m r A A
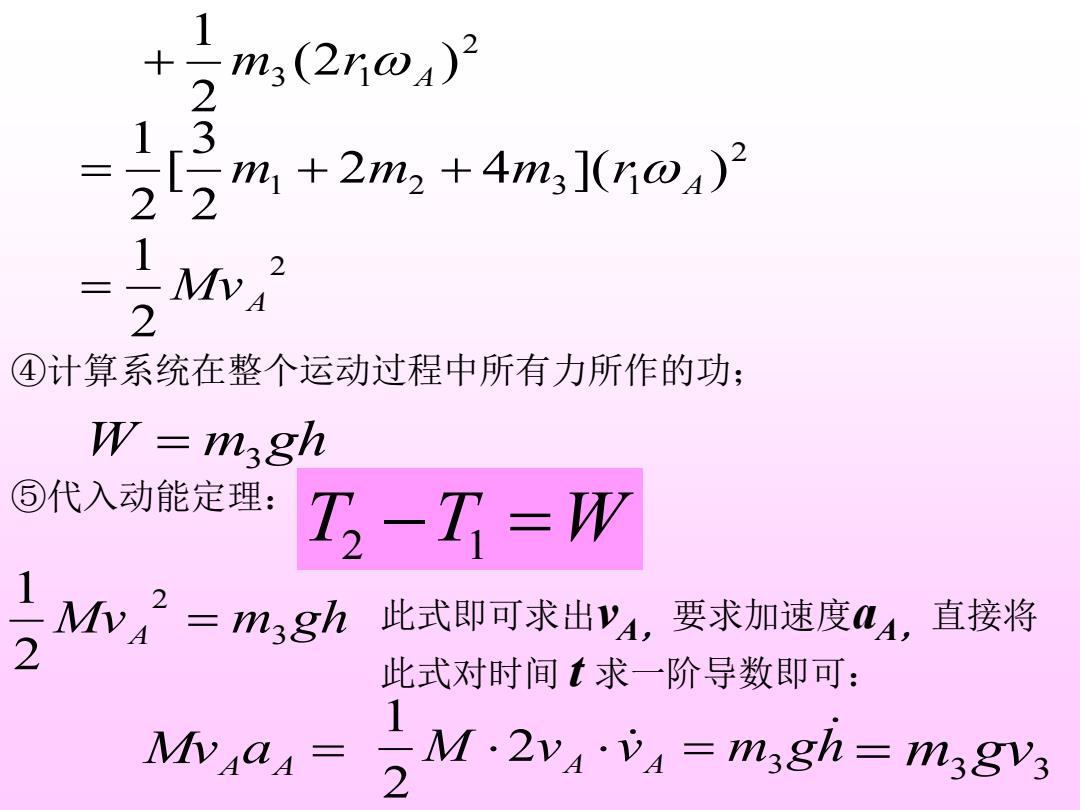
十 二23 m3(2io4)2 1 m1+2m2+4m3](ioA)2 2 2 1 2 Mv A 2 ④计算系统在整个运动过程中所有力所作的功; W=magh ⑤代入动能定理: T-T=W 1 Mv"=m3gh 此式即可求出yA,要求加速度aA, 直接将 2 此式对时间t求一阶导数即可: 1 2 M.2vv=m3gh m3gvs
2 3 1 (2 ) 2 1 A + m r 2 1 2 3 1 2 4 ]( ) 2 3 [ 2 1 A = m + m + m r 2 2 1 = MvA ④计算系统在整个运动过程中所有力所作的功; W = m3 gh ⑤代入动能定理: T2 −T1 =W MvA m3 gh 2 2 1 = 此式即可求出vA,要求加速度aA,直接将 此式对时间 t 求一阶导数即可: MvA aA = = m3 gv3 M vA vA m gh 2 3 2 1 =
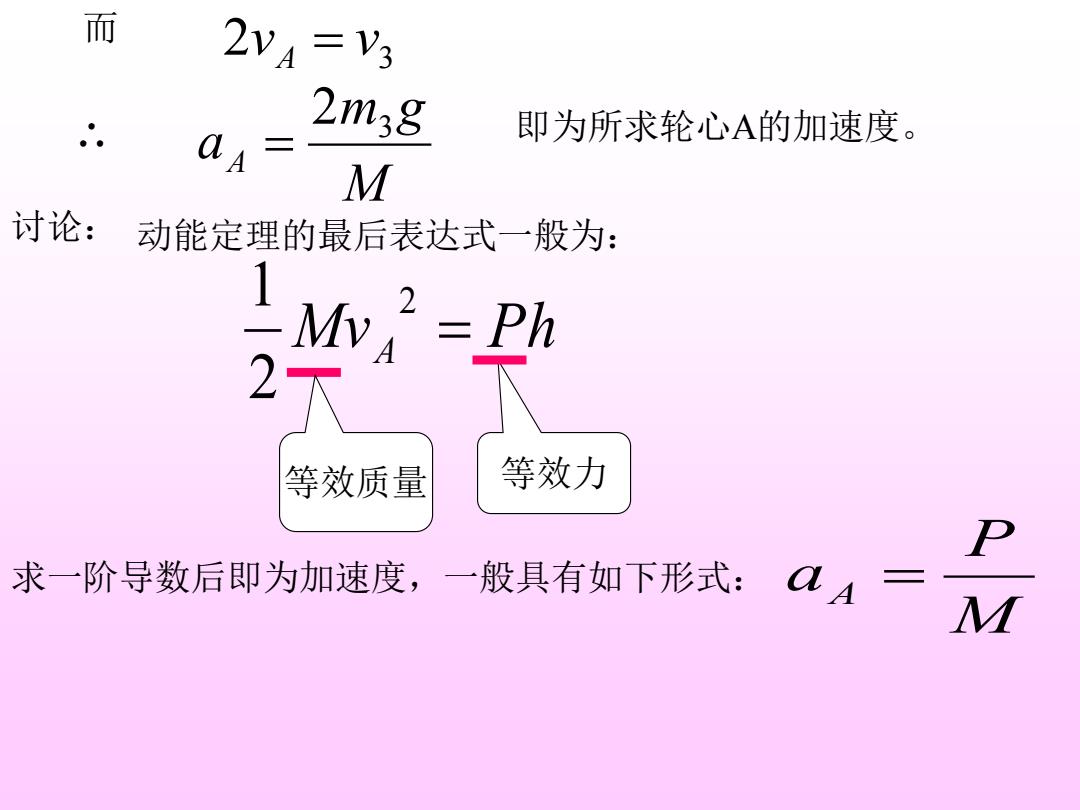
而 2v=V3 2m3g 即为所求轮心A的加速度。 a4= M 讨论:动能定理的最后表达式一般为: Mv=Ph 2下 等效质量 等效力 P 求一阶导数后即为加速度,一般具有如下形式: aA
2 3 v v 而 A = M m g aA 3 2 ∴ = 即为所求轮心A的加速度。 Mv Ph A = 2 2 1 讨论: 等效质量 等效力 动能定理的最后表达式一般为: 求一阶导数后即为加速度,一般具有如下形式: M P aA =
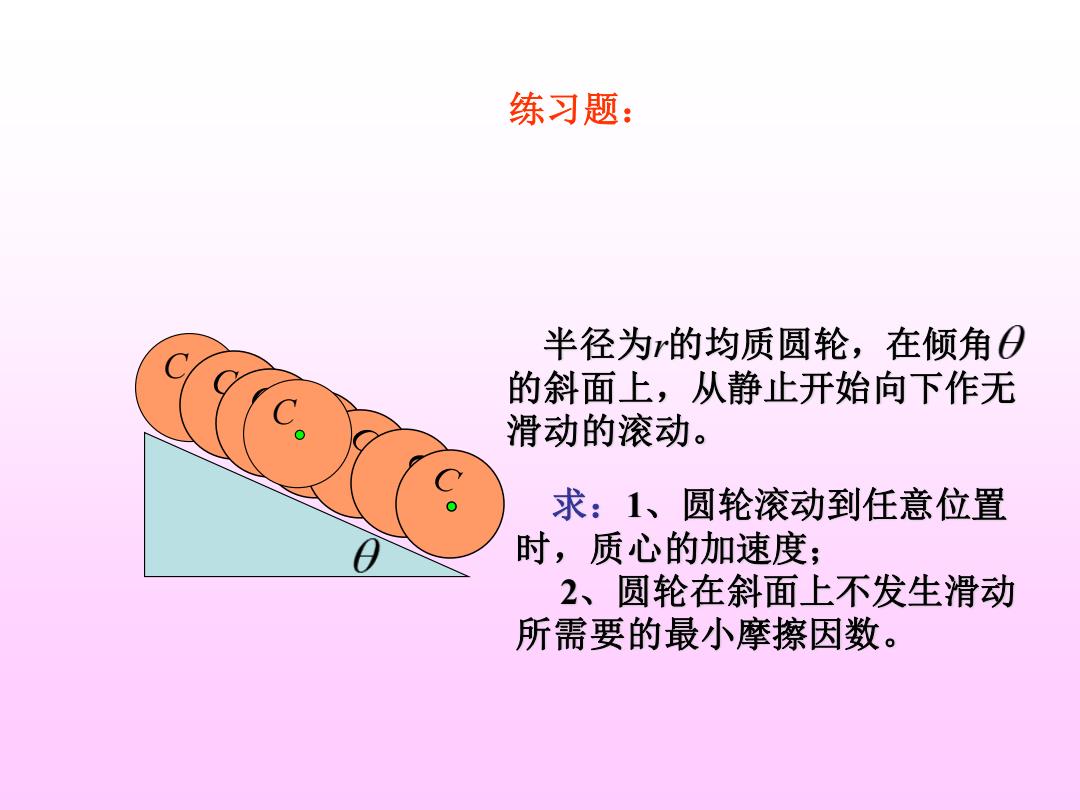
练习题: 半径为r的均质圆轮,在倾角日 的斜面上,从静止开始向下作无 滑动的滚动。 求:1、圆轮滚动到任意位置 时,质心的加速度; 2、圆轮在斜面上不发生滑动 所需要的最小摩擦因数
C 求:1、圆轮滚动到任意位置 时,质心的加速度; 2、圆轮在斜面上不发生滑动 所需要的最小摩擦因数。 C 半径为r的均质圆轮,在倾角 的斜面上,从静止开始向下作无 滑动的滚动。 练习题:

解:(1)主动力做的功 W mgSsin 0 (2)动能 T=0 Vo =r@o .1 2 3mvi=mgSsin 4 2 gsin 0 3 (3)质心运动定理 mao =mgsin e-fgcoso 380
W = mgS sin 解: (1)主动力做的功 2 2 2 2 0 1 2 1 2 1 0 o o T J m v T = + = (2)动能 0 0 v = r sin 4 3 2 0 mgS mv = sin 3 2 a0 = g (3)质心运动定理 ma0 = mgsin − fgcos f tg 3 1 =
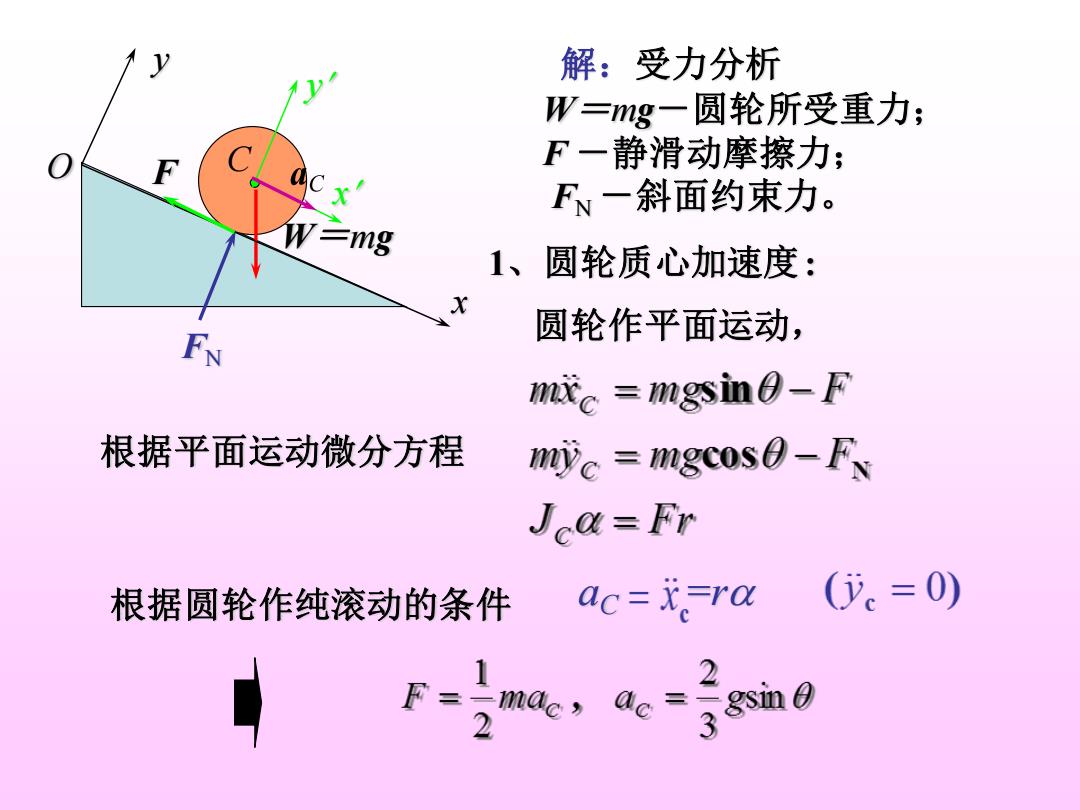
解:受力分析 W=mg一圆轮所受重力; F一静滑动摩擦力; FN一斜面约束力。 W-mg 1、圆轮质心加速度: 比 F 圆轮作平面运动, m成c=mgsin0-F 根据平面运动微分方程 mic=mgcos(0-F、 Jca=Fr 根据圆轮作纯滚动的条件 ac=t。=ra (。=0) F=mde,ae=sin 1 2
解:受力分析 C W=mg FN 1、圆轮质心加速度: W=mg-圆轮所受重力; F -静滑动摩擦力; x FN -斜面约束力。 y x y O F 根据平面运动微分方程 圆轮作平面运动, 根据圆轮作纯滚动的条件 aC =r
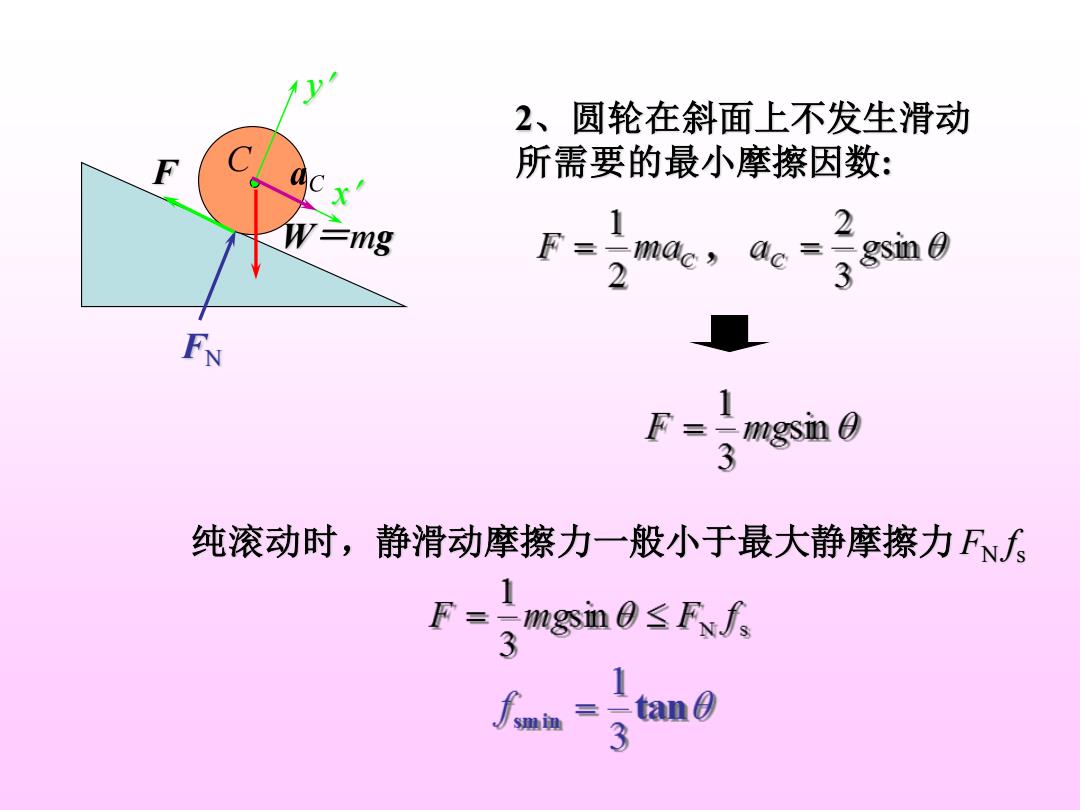
2、圆轮在斜面上不发生滑动 所需要的最小摩擦因数: W=mg 2 F-imde,de-sin 2 FN 1 F=。mgsin0 3 纯滚动时,静滑动摩擦力一般小于最大静摩擦力F∫ F=-mgin0≤Ffs 3
2、圆轮在斜面上不发生滑动 所需要的最小摩擦因数: 纯滚动时,静滑动摩擦力一般小于最大静摩擦力FN f s C W=mg FN x y F

应用动能定理解题的步骤: (1)明确分析对象,一般以整个系统为研究对象: (2)分析系统的受力,区分主动力与约束力, 在理想约束的情况下约束力不做功: (3)分析系统的运动,计算系统在任意位置的动能 或在起始和终了位置的动能; (4)应用动能定理建立系统的动力学方程,而后求解; (5)对问题的进一步分析与讨论
(5)对问题的进一步分析与讨论。 应用动能定理解题的步骤: (1)明确分析对象,一般以整个系统为研究对象; (2)分析系统的受力,区分主动力与约束力, 在理想约束的情况下约束力不做功; (3)分析系统的运动,计算系统在任意位置的动能 或在起始和终了位置的动能; (4)应用动能定理建立系统的动力学方程,而后求解;
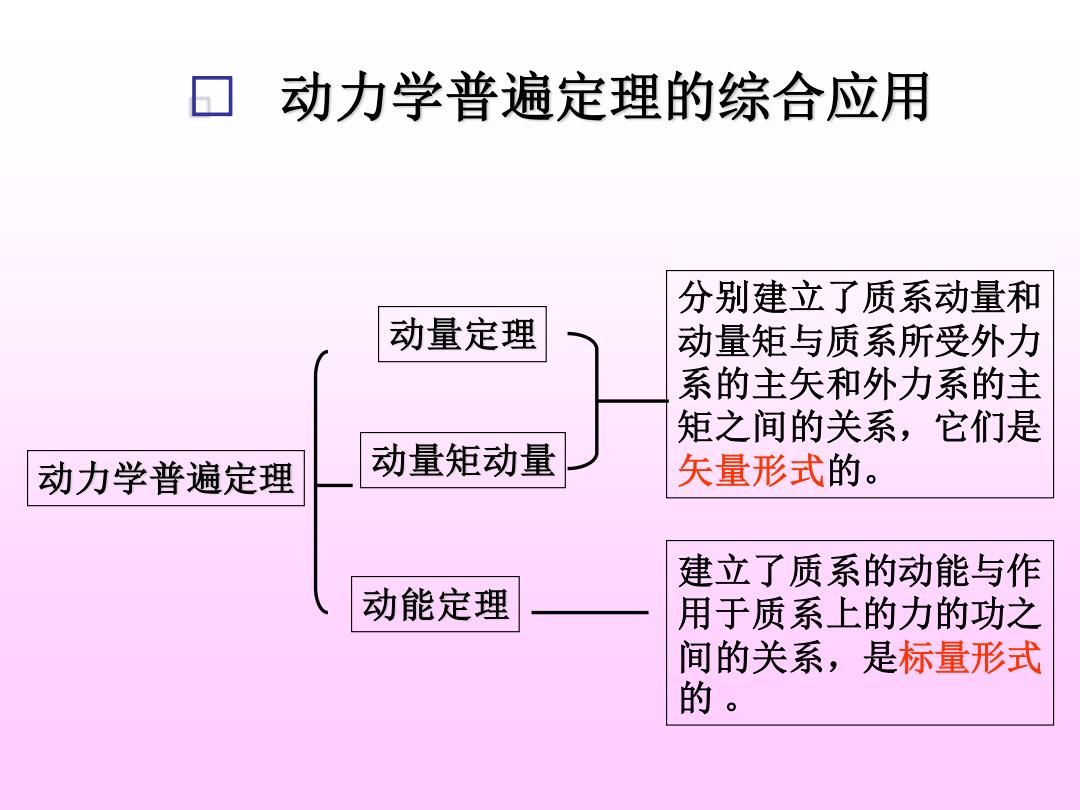
□ 动力学普遍定理的综合应用 分别建立了质系动量和 动量定理 动量矩与质系所受外力 系的主矢和外力系的主 矩之间的关系,它们是 动力学普遍定理 动量矩动量 矢量形式的。 建立了质系的动能与作 动能定理 用于质系上的力的功之 间的关系,是标量形式 的
动力学普遍定理 动量定理 动量矩动量 动能定理 □ 动力学普遍定理的综合应用 分别建立了质系动量和 动量矩与质系所受外力 系的主矢和外力系的主 矩之间的关系,它们是 矢量形式的。 建立了质系的动能与作 用于质系上的力的功之 间的关系,是标量形式 的