
第6章↓ 点的运动学 ★矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例
第6章 点的运动学 ★ 矢量法 ★ 直角坐标法 ★ 自然(弧坐标)法 ★ 应用举例

§6-1 运动学的基本概念 非运动学:以几何观点(几何公理)研究物体的运 动(轨迹,速度和加速度),不考虑物体运动的原因. 固定参考系:一般采用固连于地球上的坐标系为 参考系,称为固定参考系。 参照物--参考体--参考坐标系---参考系 对任何物体运动的描述都是相对的。 +时间:瞬时和时间间隔 瞬时 时间间隔
运动学: 以几何观点(几何公理)研究物体的运 动(轨迹,速度和加速度), 不考虑物体运动的原因. §6-1 运动学的基本概念 固定参考系: 一般采用固连于地球上的坐标系为 参考系,称为固定参考系. 时间: 瞬时和时间间隔 瞬时 时间间隔 t1 t t2 t 参照物-----参考体------参考坐标系------参考系 对任何物体运动的描述都是相对的

点:就是指不计其形状、大小、只在空间占有确 定位置的几何点 刚体:可看作由无穷多个点的组成的不变形的几何 体。 直线运动 曲线运动
刚体:可看作由无穷多个点的组成的不变形的几何 体。 点:就是指不计其形状、大小、只在空间占有确 定位置的几何点 直线运动 曲线运动
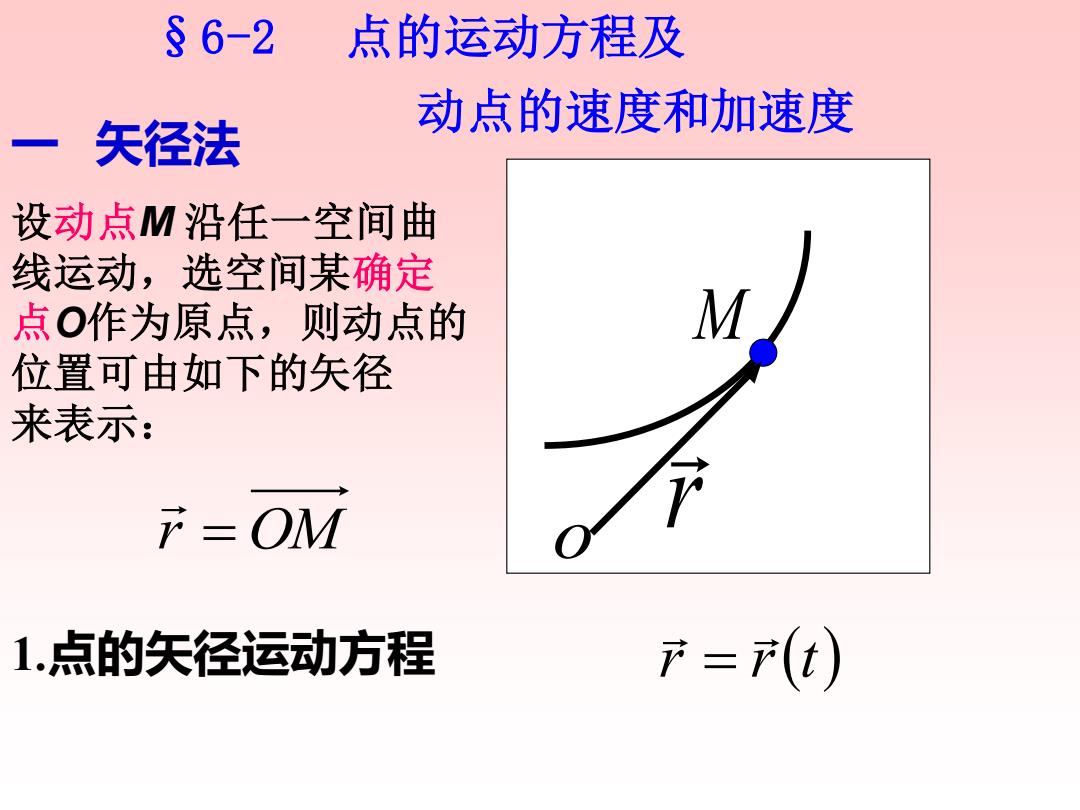
§6-2 点的运动方程及 动点的速度和加速度 一矢径法 设动点M沿任一空间曲 线运动,选空间某确定 点O作为原点,则动点的 位置可由如下的矢径 来表示: r OM 1.点的矢径运动方程 产=(t)
§6-2 点的运动方程及 动点的速度和加速度 一 矢径法 r = OM 1.点的矢径运动方程 r r(t) = 设动点M 沿任一空间曲 线运动,选空间某确定 点O作为原点,则动点的 位置可由如下的矢径 来表示: o M r
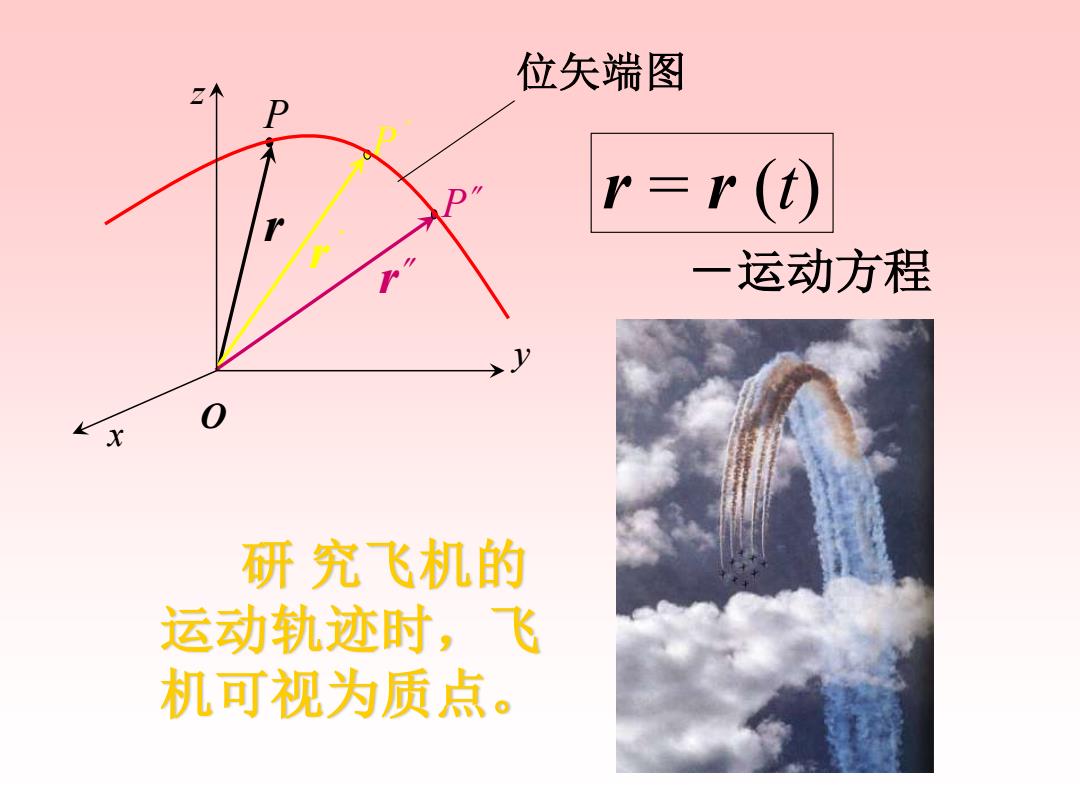
位矢端图 2个 r=r(t) 一运动方程 研究飞机的 运动轨迹时,飞 机可视为质点
r r ´ r r = r (t) P P´ P x z y O -运动方程 位矢端图 研 究飞机的 运动轨迹时,飞 机可视为质点

2.点的速度(定义): 速度(velocity) 点在瞬时运动快慢和运动方向的力学量。 dr 速度的方向沿着运动轨迹的切线: ) dt 指向与点的运动方向一致; 速度大小等于矢量的模。 3.点的加速度(定义): 加速度(acceleration) 描述点在瞬时速度大小和方向 变化率的力学量。 do d'r a 加速度的方向为△的极限方向 dt dt2 (指向与轨迹曲线的凹向一致) 加速度大小等于矢量的模
2.点的速度(定义): t r d d = t a d d = 2 2 d d t r = 3.点的加速度(定义): 速度(velocity) 速度大小等于矢量的模。 指向与点的运动方向一致; 速度的方向沿着运动轨迹的切线; 点在t瞬时运动快慢和运动方向的力学量。 加速度(acceleration) 加速度大小等于矢量a的模。 加速度的方向为v的极限方向 (指向与轨迹曲线的凹向一致) 描述点在t瞬时速度大小和方向 变化率的力学量

小结 (1)矢径r,运动方程 r=r() (2)轨迹-矢端曲线 (3)有限位移 dr=r(i+4t)-r( (4)速度 p= dr dt (5)加速度 dv d'r a= dt2
小结

二直角坐标法 设动点M在空间运动,它在空间任一瞬时的位置也可用 一个固体的直角坐标系的三个坐标x,y,z来确定: 1.点的运动方程x=f(t) y=f(t) M z=6(t) F=xi+yj+z水 Y(t) (解析式)
二 直角坐标法 设动点M 在空间运动,它在空间任一瞬时的位置也可用 一个固体的直角坐标系的三个坐标x, y, z来确定: 1. 点的运动方程 x f (t) = 1 y f (t) = 2 z f (t) = 3 ( ) i j k 解析式 r = x + y + z O M r z(t) y(t) x(t) z y x

2.点的速度: F=xi+yj+zk d = dt i+业j+出+i++z水 d dt dt (Oz)为定参考系 i-j-k-0 =可+可,+ M -vitvj+v.k (t)i x(t) ) 2 2 二 Vx +,2+u
2. 点的速度: i j k r = x + y + z t r d d = k xi yj zk d d j d d i d d = + + + + + t z t y t x 2 2 2 = x + y + z x y z v v v v = + + i j k x y z v = v + v + v O M r z y x z(t) y(t) x(t) i = j = k = 0 (Oxyz)为定参考系

3.点的加速度: B=vitv,j+ok dv a- di+业j+d dt d dt dt 0 J+ dt dt dt M a-a,i+a,j+ak x(t) X () a-jas2+a 2 +az
t a d d = 2 2 2 a = ax + ay + az i j k =x + y +z 3. 点的加速度: k d d j d d i d d t t t a x y z = + + k d d j d d i dt d t t x y z = + + i j k a = ax + ay + az O M r z y x z(t) y(t) x(t)