
第三章平面任意力系 作业讲评 1力线平移定理 2平面任意力系向一点简化,主矢和主矩 3分布荷载 习4平面任意力系的平衡条件和平衡方程 2018年3月22日
第三章 平面任意力系 作业讲评 1 力线平移定理 2 平面任意力系向一点简化,主矢和主矩 3 分布荷载 4 平面任意力系的平衡条件和平衡方程 2018年3月22日
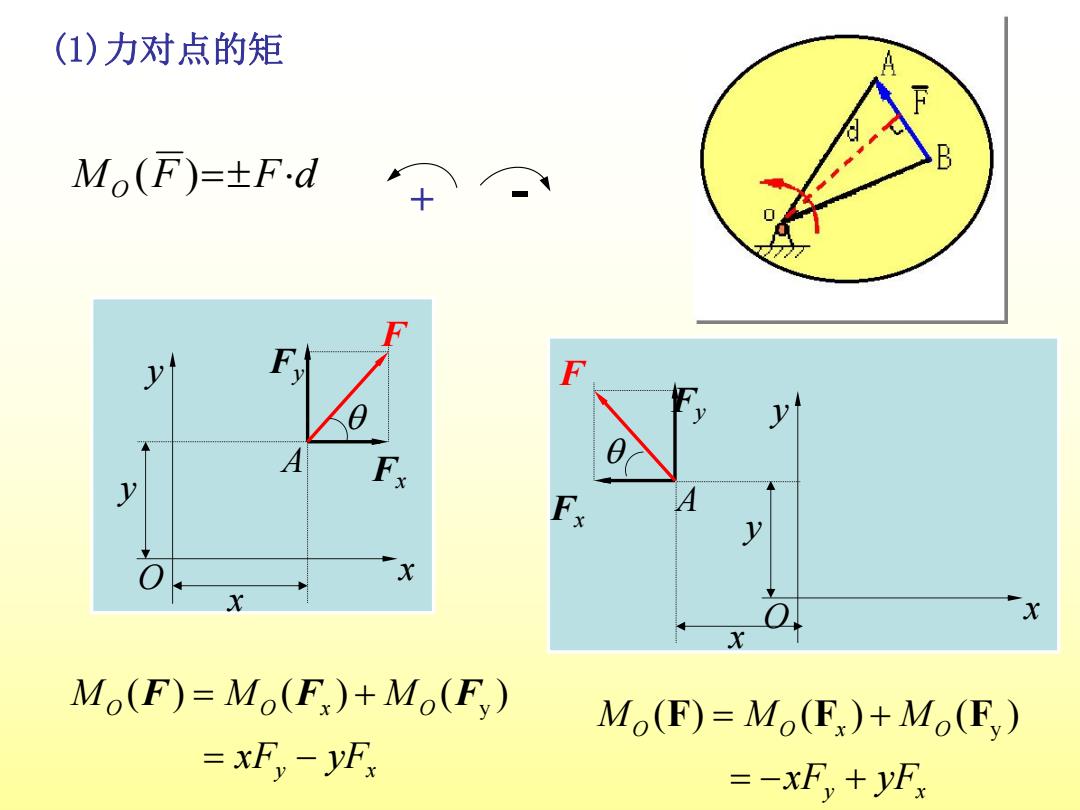
(1)力对点的矩 Mo(F)=±F.d y F y A y Fx y X X Mo(F)=Mo(F)+Mo(F) Mo(F)=Mo(F)+Mo(F) =xF-yF =-xF,+yF
MO (F )Fd (1)力对点的矩 + - y x O O x O xF yF M M M ( ) ( ) ( ) F F Fy O y x A y x Fy Fx F q O y x y x A Fy Fx F q y x O O x O xF yF M M M ( ) ( ) ( ) F F Fy
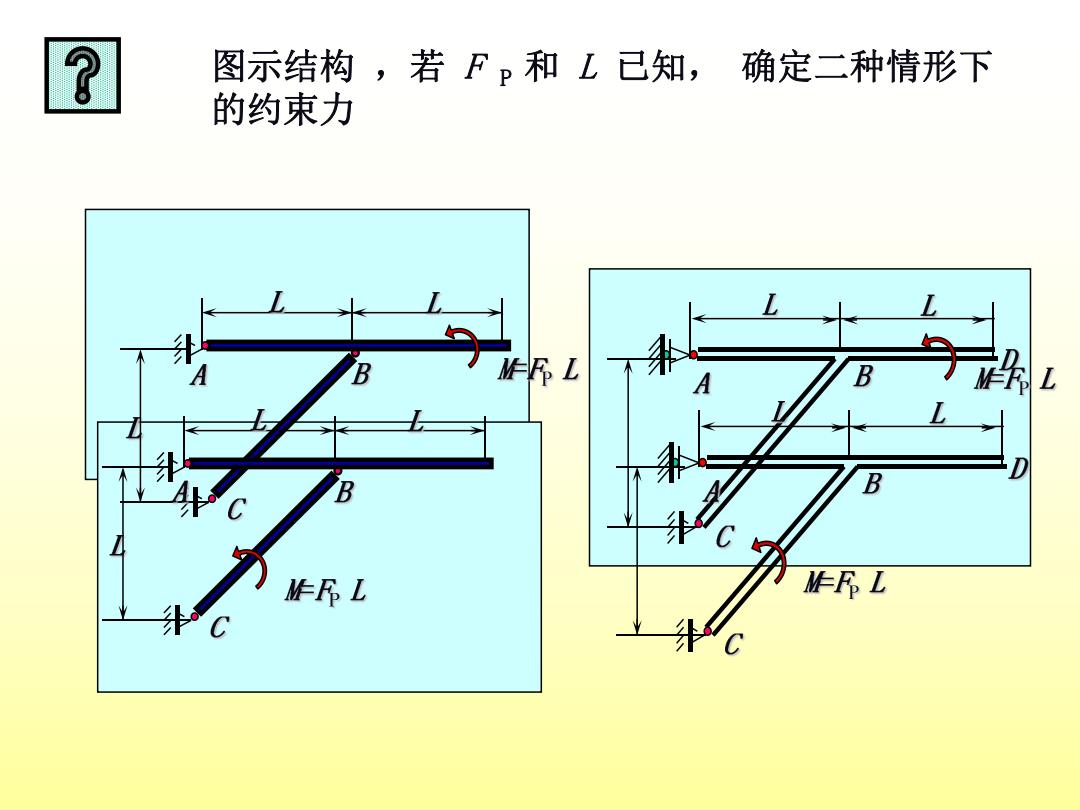
3 图示结构,若Fp和L已知,确定二种情形下 的约束力 作RL B 作FL 作FL
图示结构 ,若 F P 和 L 已知, 确定二种情形下 的约束力
§2-3 平面任意力系的简化 风力 重力 浮力 阻力
风力 浮力 重力 阻力 §2-3 平面任意力系的简化

一般力系实例 Fs FN Stringers Floor beams
一般力系实例
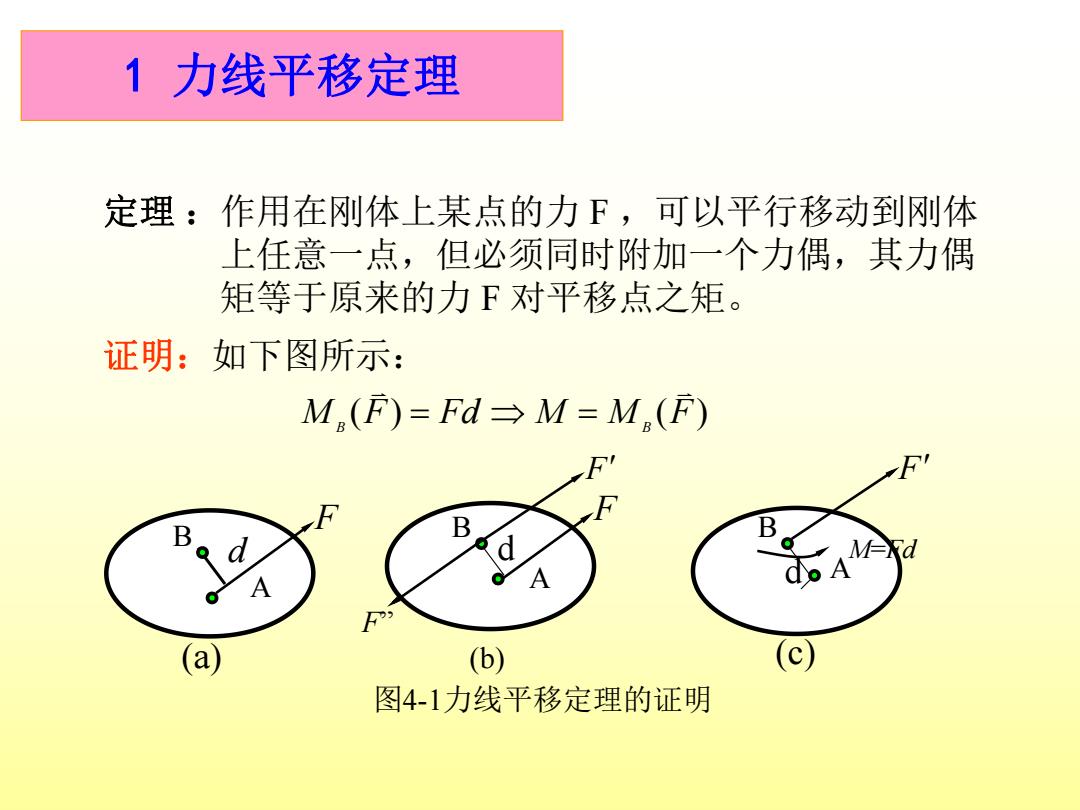
1力线平移定理 定理:作用在刚体上某点的力F,可以平行移动到刚体 上任意一点,但必须同时附加一个力偶,其力偶 矩等于原来的力F对平移点之矩。 证明:如下图所示: M(F)=Fd→M=M.(F) B B M合d A A (a) (b) (c) 图4-1力线平移定理的证明
定理 :作用在刚体上某点的力 F ,可以平行移动到刚体 上任意一点,但必须同时附加一个力偶,其力偶 矩等于原来的力 F 对平移点之矩。 证明:如下图所示: M (F) Fd M M (F) B B 1 力线平移定理 (a) A B d F A B d F F” (b) 图4-1力线平移定理的证明 B d AM=Fd (c) F F

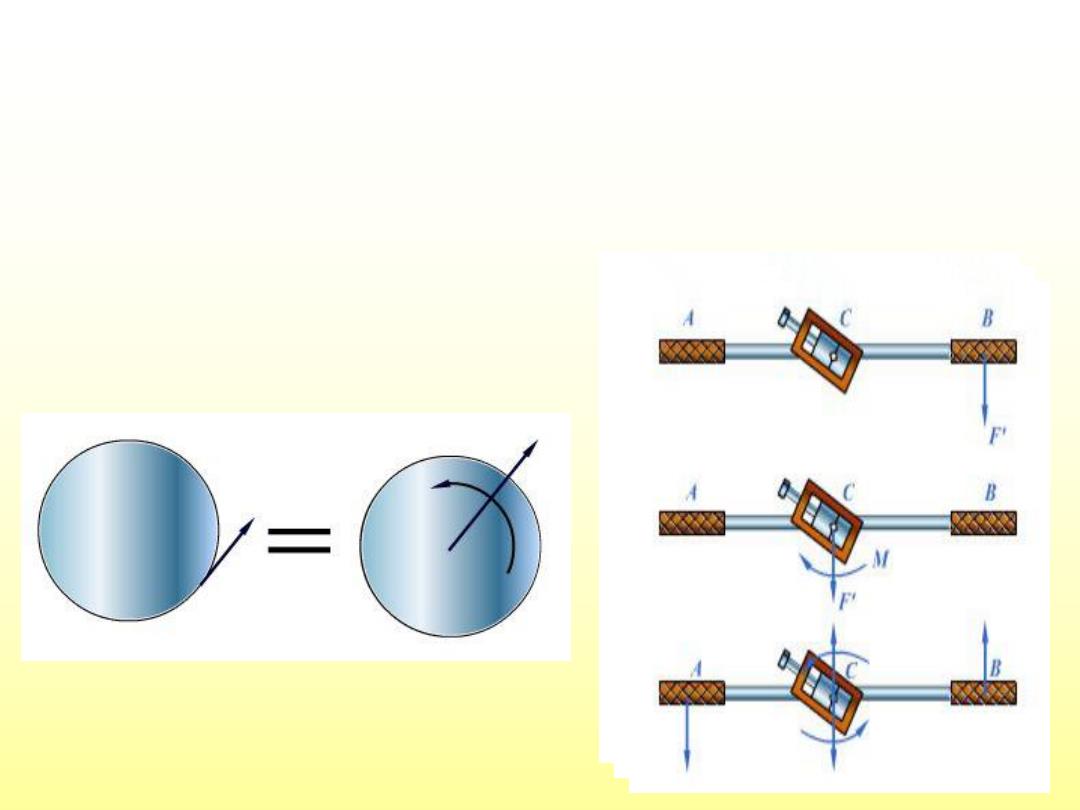
可见,一个力可以分解为一个与其等值平行的力和一 个位于平移平面内的力偶。反之,一个力偶和一个位于该 力偶作用面内的力,也可以用一个位于力偶作用面内的力 来等效替换 如打乒乓球,若球拍对球作用的力其作用线通过球心 (球的质心),则球将平动而不旋转;但若力的作用线与 球相切一“削球”,则球将产生平动和转动。 (a) (b) 图4-2
可见,一个力可以分解为一个与其等值平行的力和一 个位于平移平面内的力偶。反之,一个力偶和一个位于该 力偶作用面内的力,也可以用一个位于力偶作用面内的力 来等效替换 如打乒乓球,若球拍对球作用的力其作用线通过球心 (球的质心),则球将平动而不旋转;但若力的作用线与 球相切——“削球” ,则球将产生平动和转动。 c F c F c m 图4-2 (a) (b) F
A C B 网 F B 三 B
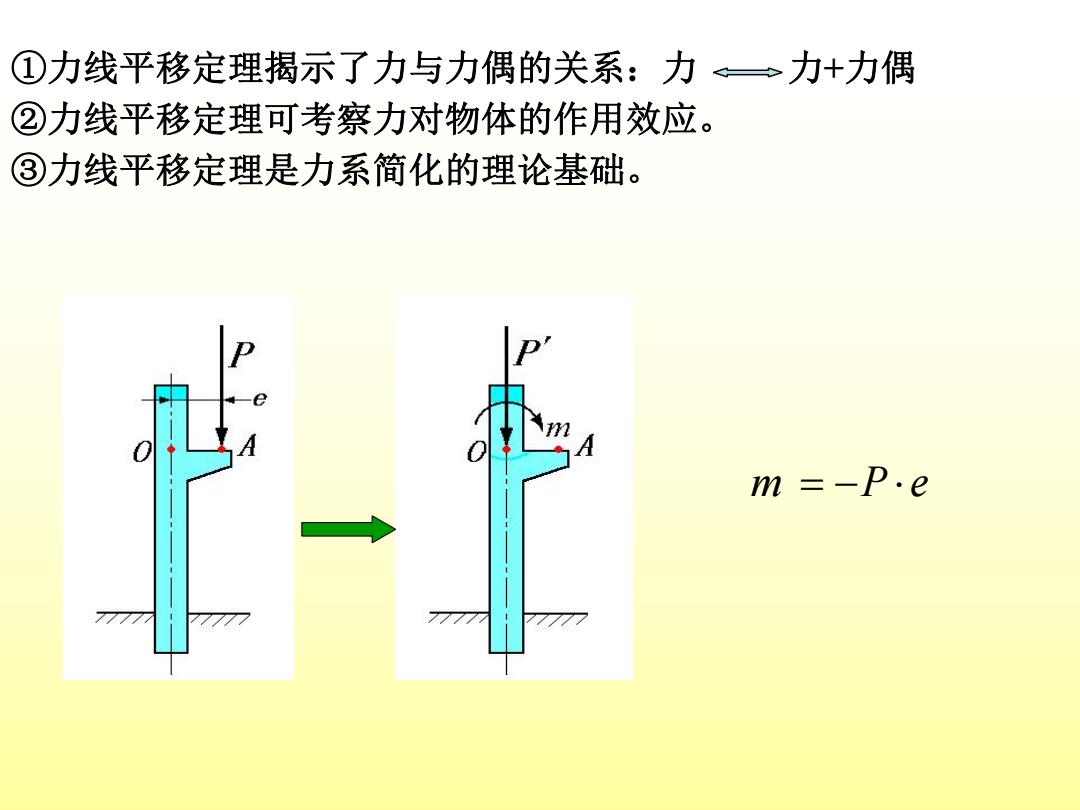
①力线平移定理揭示了力与力偶的关系:力。心力+力偶 ②力线平移定理可考察力对物体的作用效应。 ③力线平移定理是力系简化的理论基础。 m =-P.e
①力线平移定理揭示了力与力偶的关系:力 力+力偶 ②力线平移定理可考察力对物体的作用效应。 m P e ③力线平移定理是力系简化的理论基础
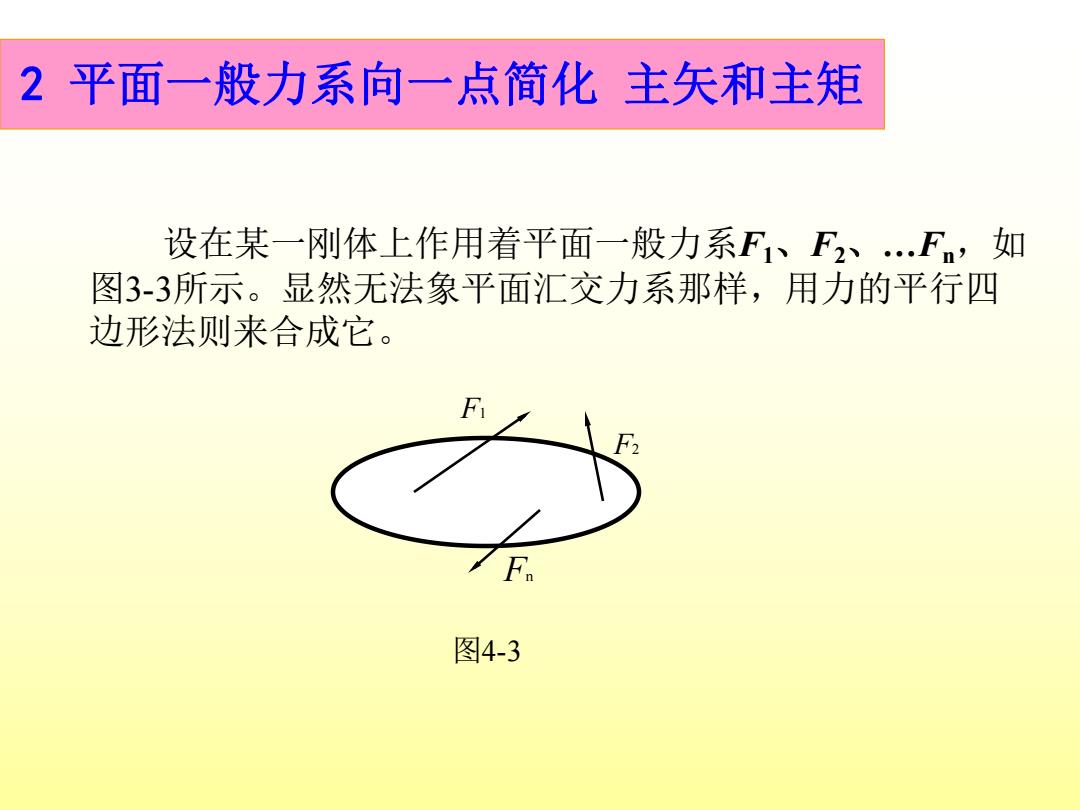
2平面一般力系向一点简化主矢和主矩 设在某一刚体上作用着平面一般力系F、F2、.Fn,如 图3-3所示。显然无法象平面汇交力系那样,用力的平行四 边形法则来合成它。 图4-3
F1 F2 Fn 图4-3 设在某一刚体上作用着平面一般力系F1、F2、…Fn,如 图3-3所示。显然无法象平面汇交力系那样,用力的平行四 边形法则来合成它。 2 平面一般力系向一点简化 主矢和主矩