
佛山科学技术学院2016~2017学年第二学期 《理论力学》课程期末考试试题解答及评分标准(E) 专业、班级:土木工程系 任课教师: 一.选择题,每题2分,共10分 1、A,2、B,3、B,4、B,5、D 二、(1) 【解答】 由对称性可知yc=0 而xc= ∑sx ∑s 由已知S1=S2=4000mm2,S3=3000mm3 x1=-10mm,x?=100mm,x3=210mm 代入方程,求得xc=90mm (6分) (2)解:质心的速度v=mw 所以系统的动量为p=2m=2mnv(4分) 对0点的转动惯量为:J=m2a'+ 12m2a'+ma2=8 对0点的动量矩为:L==8maw (4分) 三、解以整体为研究对象,受力图如下: D E D B (a) (b) (c) ∑F=0,F=0 ∑Me(F)=0,-FX2a-M=0 将得R=0,-一出 (4分) 以杆DEF为研究对象,受力如图. ∑Me(F-0,Fm·a-M=0 第得P。=4 (4分) 共4页第1页
佛山科学技术学院 2016~2017 学年第 二 学期 《理论力学》课程期末考试试题解答及评分标准 (E) 专业、班级: 土木工程系 任课教师: 一.选择题,每题 2 分,共 10 分 1、A, 2、B, 3、B,4、B, 5、D 二、(1) (6 分) (2)解:质心的速度 v aw = 所以系统的动量为 p mv maw = = 2 2 (4 分) 对 O 点的转动惯量为: 1 1 8 2 2 2 2 (2 ) (2 ) 3 12 3 J m a m a ma ma = + + = 对 O 点的动量矩为: 8 2 3 L Jw ma w = = (4 分) 三、解 以整体为研究对象,受力图如下: (4 分) (4 分) 共 4 页第 1 页
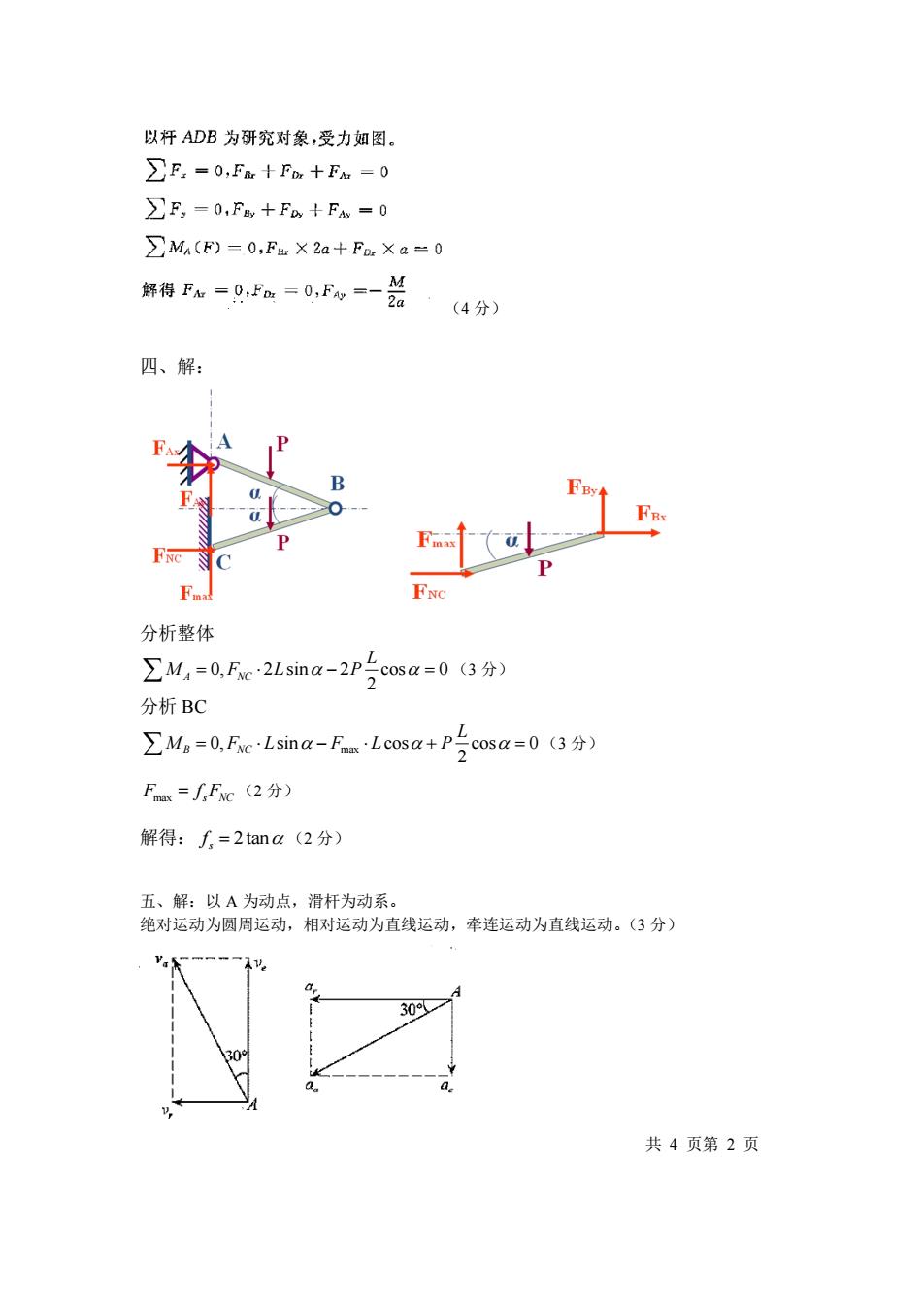
以杆ADB为研究对象,受力如图。 ∑P,=0,Fm十F,十Fa=0 ∑F,=0,PF+F+FA-0 >MA(F)=0,Fu X 2a+For Xa-0 邻得Pa=0Fa=0,Fw=一兰 ·(4分) 四、解: B FBs FNc 分析整体 ∑M4=0,Fc·2 Lsina-2p5。 cosa=0(3分) 分析BC ∑Ma=0,FcLsina-FLcosa+posa=0(3分) ) F=fFc(2分) 解得:f,=2tana(2分) 五、解:以A为动点,滑杆为动系。 绝对运动为圆周运动,相对运动为直线运动,牵连运动为直线运动。(3分) 30 30 共4页第2页
(4 分) 四、解: 分析整体 0, 2 sin 2 cos 0 2 A NC L M F L P = − = (3 分) 分析 BC max 0, sin cos cos 0 2 B NC L M F L F L P = − + = (3 分) F f F max = s NC (2 分) 解得: 2 tan s f = (2 分) 五、解:以 A 为动点,滑杆为动系。 绝对运动为圆周运动,相对运动为直线运动,牵连运动为直线运动。(3 分) 共 4 页第 2 页

(1)速度=.十℃, ea=w·QA=0.2m/s =4c030°=0.2X9=0.173m/3 (4分) (2)加速度:a。=a,十a, a.=a8=2·0A=0.52X0.4=0.1m/s2 a。=aa·sin30°=0.05m/s2 (4分) 六、解 【解答】 分别研究AB,BD 对AB Jna1 =Fil 对BD Joa:=F合+F台 mao F-Fg (6分) 运动学关系 an =a:l n=an十a:台 6F 解得a=7m= 30F 7ml (6分) 七、解:解AB杆作平面运动,在图示瞬时,因ya/ye且v4⊥ye,所以AB瞬 时平移(瞬时平动),所以 Va=v=@OA=0.4 m/s (3分) 04B=0,aB4=0 B 轮B做纯滚动,所以 @Bc =Va/r=8 rad/s (2分) 又ae=d+dg4+g (a) 其中a”=o2.OA=0.8m/s2 式(a分别在x,y方向上投影: 共4页第3页
(4 分) (4 分) 六、解 (6 分) (6 分) 七、解:解 AB 杆作平面运动,在图示瞬时,因 // A B v v 且 v v A B ⊥ ,所以 AB 瞬 时平移(瞬时平动),所以 0.4 m/s 0, 0 B A n AB BA v v OA a = = = = = (3 分) 轮 B 做纯滚动,所以 / 8 rad/s BC B = = v r (2 分) 又 ( ) n t n B A BA BA a a a a = + + a 其中 2 2 0.8 m/s n A a OA = = 式 (a) 分别在 x y, 方向上投影: 共 4 页第 3 页 A B n A a B a O n BA a t BA a AB

J,-aB=-amu [1 0=-a-am (5分) ∴.ag=0 aB4=-a4=-a4=-0.8m/s2 轮纯滚动∴.&c=agr=0 AB杆平面运动 (5分) a4B=aR4/AB=-0.810.2 =-4 rad/s2 八、解:以整体为研究对象。 根据各部分的运动形式,写出系统初始和末了的动能T和T2, 系统初始静止,工=0 g 22g )-2g (3分) 计算系统在整个运动过程中所有力所作的功,W=Ps-Pssi30° (2分) 由动能定理知:T,-T=W :3p v2=Ps-Pssin30° 2g (3分) 求导, ds 6 =yA,-a+a×a=0,a4=g dt 6 (5分) 以A为研究对象, 根据质心的运动定理知: P P-T=-a 7=p-2a,2p 5 (3分) 8 6 共4页第4页
2 0 0 0.8 m/s n y B BA n t x A BA B t n n BA A A a a a a a a a a − = − = − − = = − = − = − (5 分) 2 / 0 / 0.8 / 0.2 4 rad/s BC B t AB BA a r AB a AB = = = = − = − 轮纯滚动 杆平面运动 (5 分) 八、解:以整体为研究对象。 根据各部分的运动形式,写出系统初始和末了的动能 T1 和 T2, 系统初始静止, 1 T = 0 (3 分) 计算系统在整个运动过程中所有力所作的功, 0 W Ps Ps = − sin 30 (2 分) 由动能定理知: T T W 2 1 − = ∴ 3 2 0 = sin30 2 A P Ps Ps g − ∴ = 3 A gs (3 分) (5 分) 以 A 为研究对象, 根据质心的运动定理知: A P P T a g − = ∴ 5 = 6 A P T P a P g = − (3 分) 共 4 页第 4 页