
第8章点的合成运动 §8-3牵连运动是平动时点的加速度合成定理 §8-4牵连运动为转动时点的加速度合成
第8章 点的合成运动 §8-3 牵连运动是平动时点的加速度合成定理 §8-4 牵连运动为转动时点的加速度合成
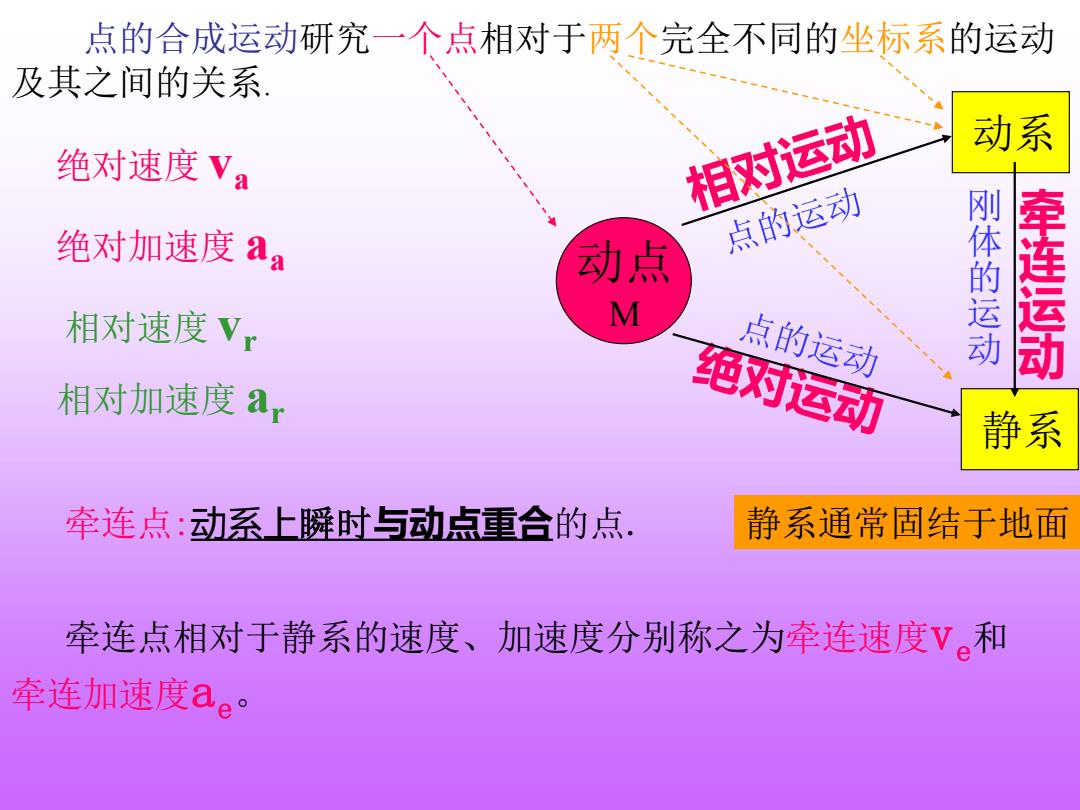
点的合成运动研究一个点相对于两个完全不同的坐标系的运动 及其之间的关系 相对运动 动系 绝对速度Va 绝对加速度aa 点的运动 动点 相对速度V, M 点的运动 刚体的运动 牵连运动 相对加速度a 绝对运动 静系 牵连点:动系上瞬时与动点重合的点 静系通常固结于地面 牵连点相对于静系的速度、加速度分别称之为牵连速度V。和 牵连加速度ae
点的合成运动研究一个点相对于两个完全不同的坐标系的运动 及其之间的关系. 牵 连 运 动 静系 动点 M 动系 刚 体 的 运 动 牵连点:动系上瞬时与动点重合的点. 绝对速度 va 绝对加速度 aa 相对速度 vr 相对加速度 ar 静系通常固结于地面 牵连点相对于静系的速度、加速度分别称之为牵连速度ve和 牵连加速度ae

求解合成运动的速度问题的一般步骤: 选取动点,动系。 三种运动的分析。 三种速度的分析。 根据速度合成定理下,=下。+下,作出速度平行四边形。 根据速度平行四边形,求出未知量
•选取动点,动系。 •三种运动的分析。 •三种速度的分析。 •根据速度平行四边形,求出未知量。 求解合成运动的速度问题的一般步骤: •根据速度合成定理 va ve vr 作出速度平行四边形。 = +

3、动点、动系选择原则 动点、动系必须分别属于两个不同的物体,否则就没有相对运 动; 动点相对动系的相对运动轨迹易于直观判断(已知绝对运动和 牵连运动求解相对运动的问题除外); 动点一般选为机构中的稳定的接触点
动点、动系必须分别属于两个不同的物体,否则就没有相对运 动; 动点相对动系的相对运动轨迹易于直观判断(已知绝对运动和 牵连运动求解相对运动的问题除外); 动点一般选为机构中的稳定的接触点. 3、动点、动系选择原则
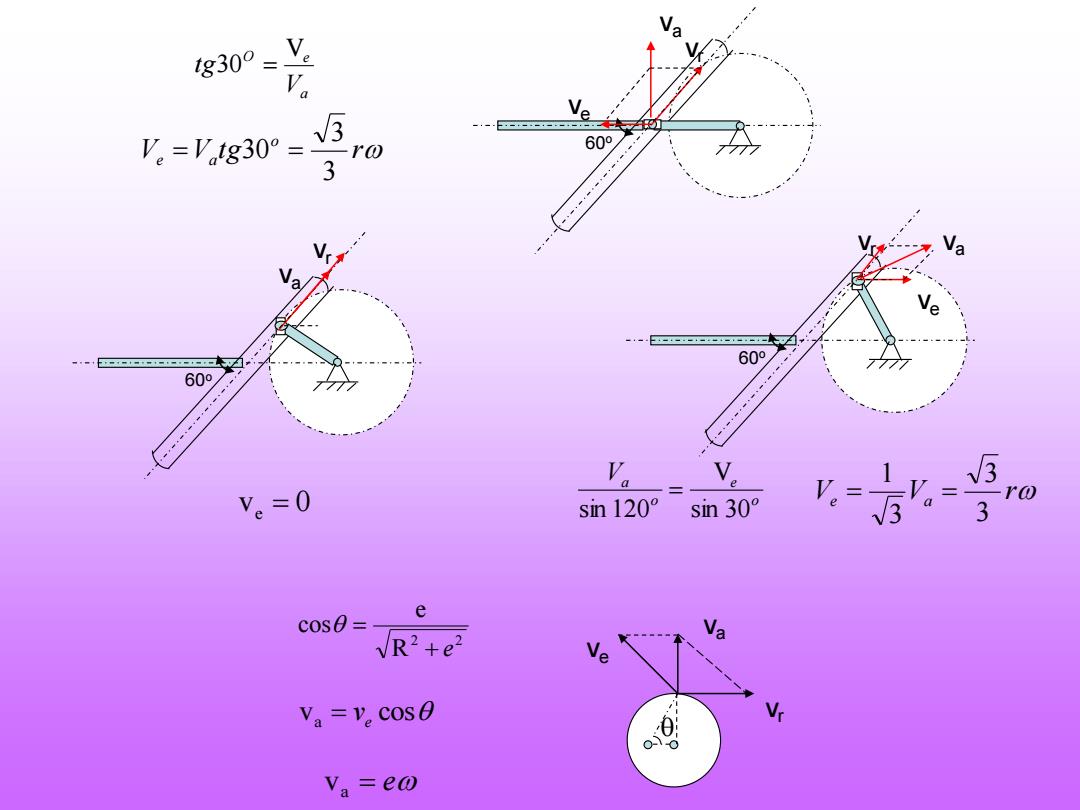
g30°=业 V e 片=,g30= 3 rw 60° e 60 60o g 1 V。=0 。= -r0 sin120° sin30° a 3 e cos0= VR2+e2 Va=V。cos0 V Va=eo
a O e V tg V 30 = 60o va ve vr V V tg r o e a 3 3 = 30 = 60o va vr 60o vr ve va ve = 0 o e o Va sin 30 V sin 120 = Ve Va r 3 3 3 1 = = va vr ve 2 2 R e cos + e = va = ve cos va = e
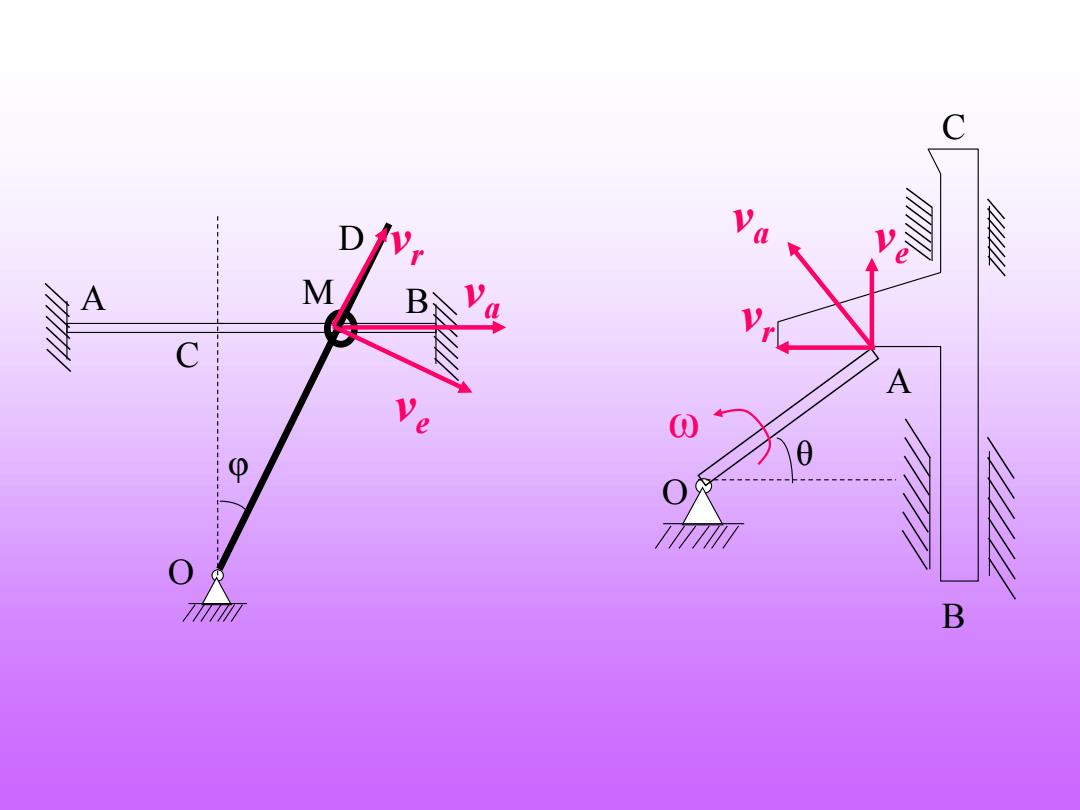
C D a M B A N 0 B
φ A B CO D M v e v a v r ω θ CB O A v avr v e

§8-3牵连运动平动时点的加速度合成定理 动点的相对速度和相对加速度 西,=++1 a,='++1 动系平动时 M 步,=置'+j+R'=a
§8-3 牵连运动平动时点的加速度合成定理 动点的相对速度和相对加速度 z x y O 动系平动时 M

区=正+吗 两边求导求加速度 。=立+, a。= 牵连加速度为 。=o=do=d。 加速度合成公式成为 dn=d。+d, 牵连运动为平动时,动点的绝对加速度等于牵连加速度 和相对加速度的矢量和
a e r v v v = + 两边求导求加速度 牵连加速度为 加速度合成公式成为 牵连运动为平动时,动点的绝对加速度等于牵连加速度 和相对加速度的矢量和
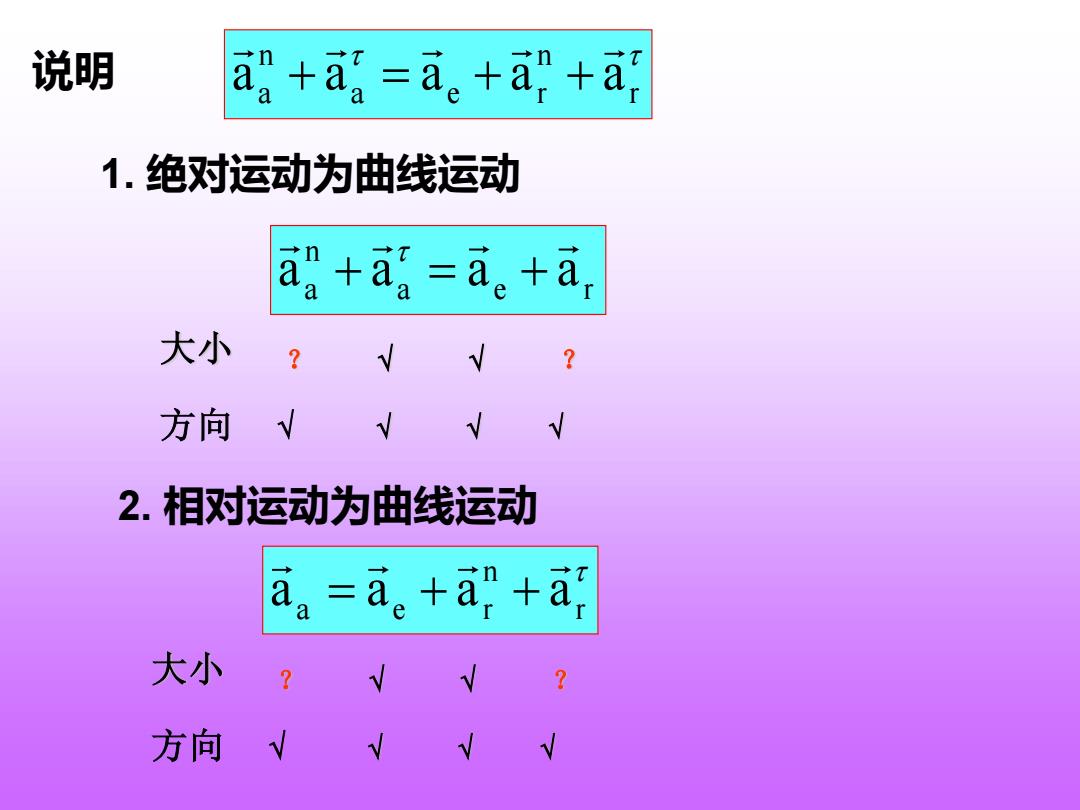
说明 a+ag=a。+a+a 1.绝对运动为曲线运动 a+a=a。+a, 大小 方向√√ 2.相对运动为曲线运动 aa=a。+a+a 大小 方向 V
说明 r n a e r n a a a a a a + = + + 1. 绝对运动为曲线运动 2. 相对运动为曲线运动 大小 ? ? 方向 a e r n a a a a a + = + 大小 ? ? 方向 r n a e r a a a a = + +
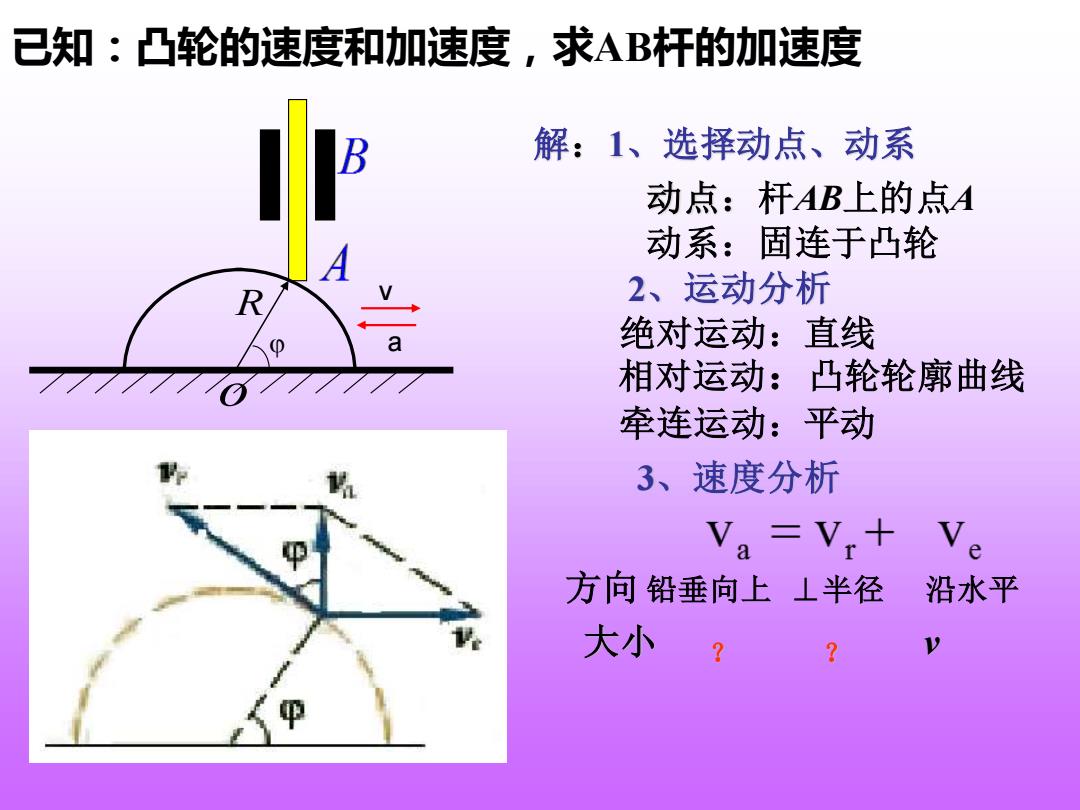
已知:凸轮的速度和加速度,求AB杆的加速度 解:1、选择动点、动系 动点:杆AB上的点A A 动系:固连于凸轮 R 2、运动分析 绝对运动:直线 相对运动:凸轮轮廓曲线 牵连运动:平动 3、速度分析 Va=V+ 方向铅垂向上⊥半径 沿水平 大小
解:1、选择动点、动系 动点:杆AB上的点A 动系:固连于凸轮 2、运动分析 绝对运动:直线 牵连运动:平动 相对运动:凸轮轮廓曲线 3、速度分析 大小 ? ? v 方向 铅垂向上 ⊥半径 沿水平 已知:凸轮的速度和加速度,求AB杆的加速度 v a o R