
第11章动量定理 §11-1基本概念 §11-2动量定理及其基本方程 §11-3质心运动定理和动量守恒
第11章 动量定理 §11-1 基本概念 §11-2 动量定理及其基本方程 §11-3 质心运动定理和动量守恒
动力学 [例1)]桥式起重机跑车吊挂一重为G的重物,沿水平横梁作匀速 运动,速度为,重物中心至悬挂点距离为L。突然刹车,重物 因惯性绕悬挂点O向前摆动,求钢丝绳的最大拉力。 解:①选重物(抽象为质点)为研究对象 ②受力分析如图所示 ③运动分析,沿以O为圆心, L为半径的圆弧摆动
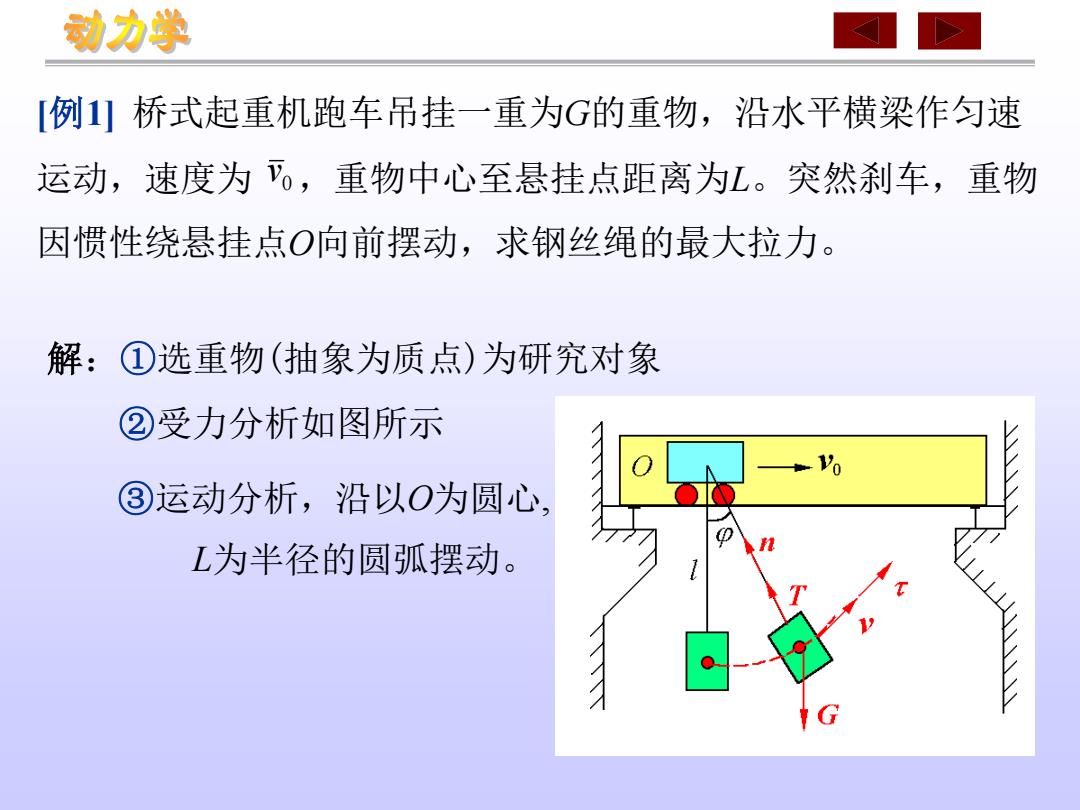
0 v [例1] 桥式起重机跑车吊挂一重为G的重物,沿水平横梁作匀速 运动,速度为 ,重物中心至悬挂点距离为L。突然刹车,重物 因惯性绕悬挂点O向前摆动,求钢丝绳的最大拉力。 解:①选重物(抽象为质点)为研究对象 ②受力分析如图所示 ③运动分析,沿以O为圆心, L为半径的圆弧摆动
动力学 ④列出自然形式的质点运动微方程 Vo ma,=∑F, Gdv =-Gsino g dt man-F, Gv2-T-Gcosp 81 ⑤求解未知量 电式得T=G(cosp+-g》 其中o,v为变量.由式知重物作减速运动,因此p=O时,T=Tmax Tm-G(1+ gl 「注]①减小绳子拉力途径:减小跑车速度或者增加绳子长度。 ②拉力Tmx由两部分组成,一部分等于物体重量,称为静拉力 一部分由加速度引起,称为附加动拉力。全部拉力称为动拉力
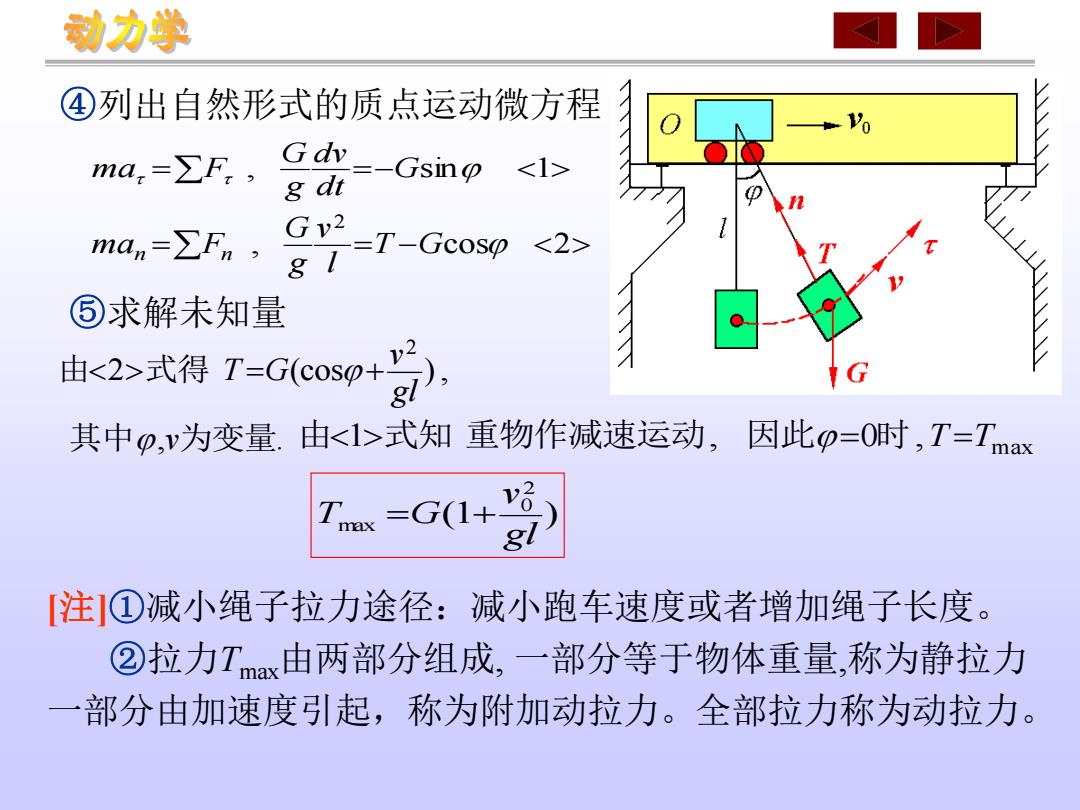
= , =−Gsin 1 dt dv g G ma F = , = − cos 2 2 T G l v g G man Fn ④列出自然形式的质点运动微方程 , . 2 (cos ), 2 其中 为变量 由 式得 v gl v T G = + max 由1式知 重物作减速运动, 因此=0时,T =T (1 ) 2 0 max gl v T =G + ⑤求解未知量 [注]①减小绳子拉力途径:减小跑车速度或者增加绳子长度。 ②拉力Tmax由两部分组成, 一部分等于物体重量,称为静拉力 一部分由加速度引起,称为附加动拉力。全部拉力称为动拉力
例一圆锥摆,如图所示。质量m=0.1kg的小球系于 长=0.3m的绳上,绳的另一端系在固定点O,并与铅直线成 0=60°角。如小球在水平面内作匀速圆周运动,求小球 的速度v与绳的张力。 已知:m=0.1kg ,1=0.3m,0=60°,求y,F
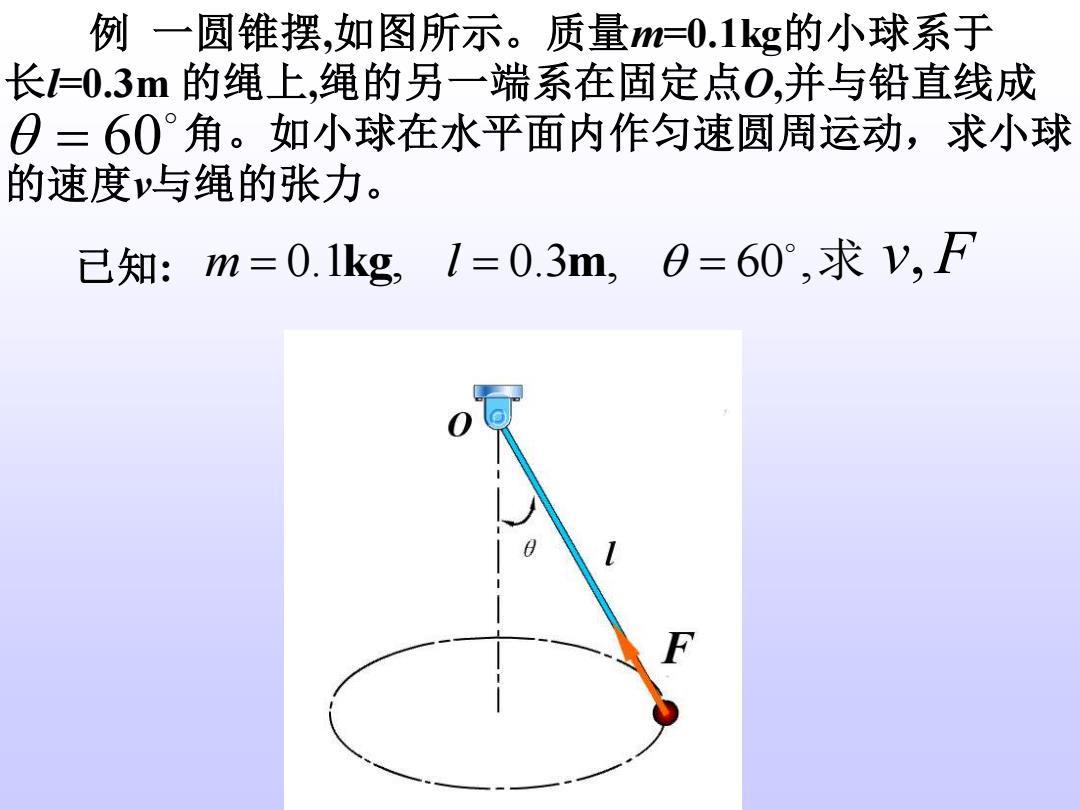
例 一圆锥摆,如图所示。质量m=0.1kg的小球系于 长l=0.3m 的绳上,绳的另一端系在固定点O,并与铅直线成 角。如小球在水平面内作匀速圆周运动,求小球 的速度v与绳的张力。 = 60 已知: m = 0.1kg, l = 0.3m, = 60 ,求 v, F
解:研究小球(任意时刻列, man=∑Fmm=Fsin 0 R 0=∑F, 0=F)=Fcose-mg 其中R=lsin0, 解得 F= mg=1.96N cos 0 FIsin20 mg v= =2.1m m 0 这是混合问题
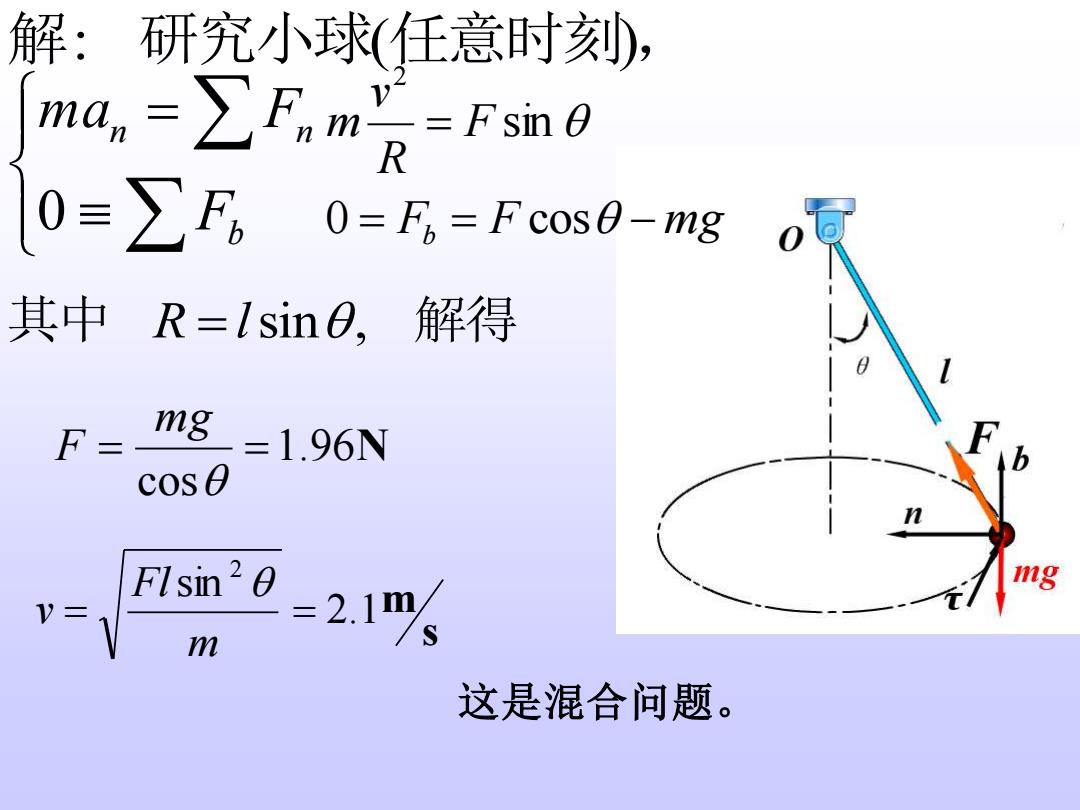
解: 研究小球(任意时刻), 其中 R l = sin , 解得 1.96N cos = = mg F s sin 2.1 m 2 = = m Fl v 这是混合问题。 = b n n F ma F 0 F F mg F R v m = b = − = 0 cos sin 2

§11-1基本概念 一、动量 1.动量的定义 (1)质点的动量质点的质量m与速度v的乘积mv称为该质点的动量。 (2)质点系的动量 质点系内各质点的动量的矢量和称为该质点系的动量主矢,简称为 质点系的动量。并用p表示,即有 p=∑my 动量是度量物体机械运动强弱程度的一个物理量。 枪弹:速度大,质量小;船:速度小,质量大。 (3)质点系动量的投影式 以px,p,和p分别表示质点系的动量在固定直角坐标轴x,y和z 上的投影。则有 px=∑myx,p=∑myiv,p2=∑mya
质点的质量 m 与速度 v 的乘积 mv 称为该质点的动量。 p= ∑mivi px = ∑mivix , py = ∑mi viy , pz = ∑miviz 以 px,py和 pz分别表示质点系的动量在固定直角坐标轴 x,y 和 z 上的投影。则有 1. 动量的定义 (1) 质点的动量 质点系内各质点的动量的矢量和称为该质点系的动量主矢,简称为 质点系的动量。并用p 表示,即有 (2) 质点系的动量 (3) 质点系动量的投影式 一、动 量 §11-1 基本概念 动量是度量物体机械运动强弱程度的一个物理量。 枪弹:速度大,质量小; 船:速度小,质量大

2.质点系动量的简捷求法 质点系的质心C的矢径表达式可写为 ∑mH:=mrc 当质点系运动时,它的质心一般也是运动的,将上式两端对时间求导 数,即得 p=∑m,y=mvc 投影到各坐标轴上有 px=∑m,yx=mvc py=∑n,yy=mvcy p:=>miviz =mvca 可见,质点系的动量,等于质点系的总质量与质心速度的乘积
质点系的质心C 的矢径表达式可写为 ∑mi ri = m rC 当质点系运动时,它的质心一般也是运动的,将上式两端对时间求导 数,即得 p = ∑mivi= mvC 2. 质点系动量的简捷求法 px = ∑mivix = mvCx py = ∑miviy = mvCy pz = ∑miviz =mvCz 投影到各坐标轴上有 可见,质点系的动量,等于质点系的总质量与质心速度的乘积
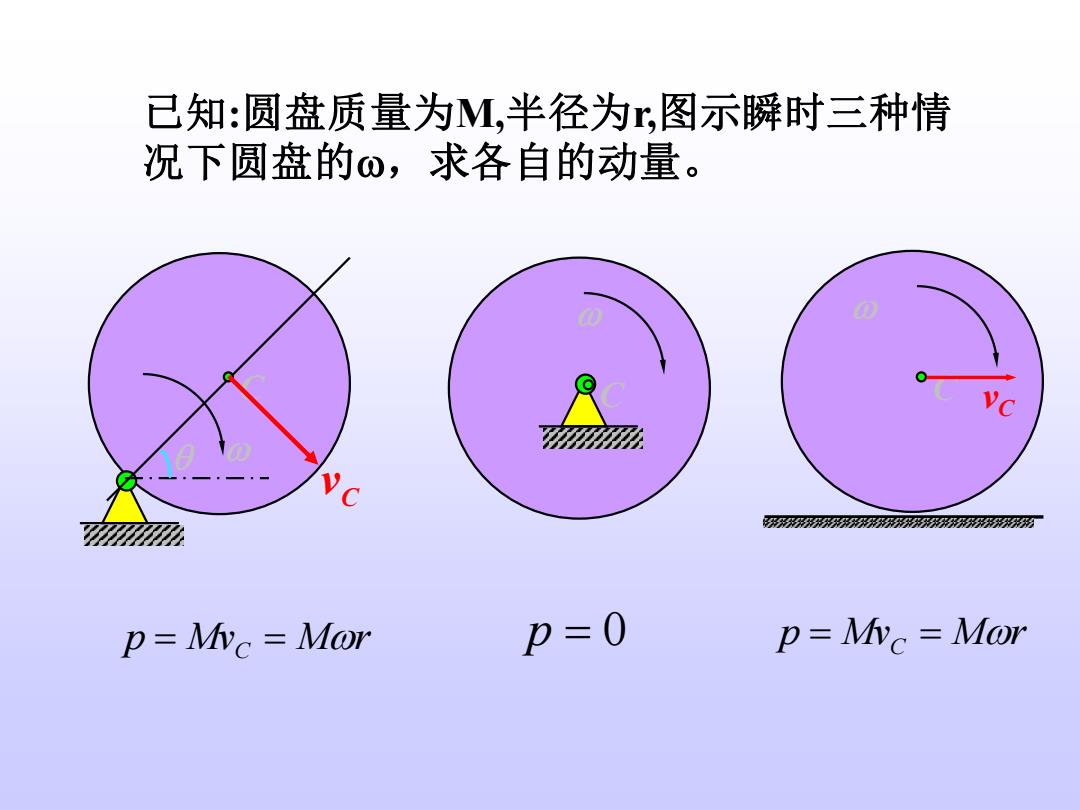
已知:圆盘质量为M,半径为r,图示瞬时三种情 况下圆盘的o,求各自的动量。 外外界外朵界外州外涮 p=Mvc Mor 0 p=Mvc Mor
C C v 已知:圆盘质量为M,半径为r,图示瞬时三种情 况下圆盘的,求各自的动量。 C C vC p Mv M r = C = p = 0 p Mv M r = C =
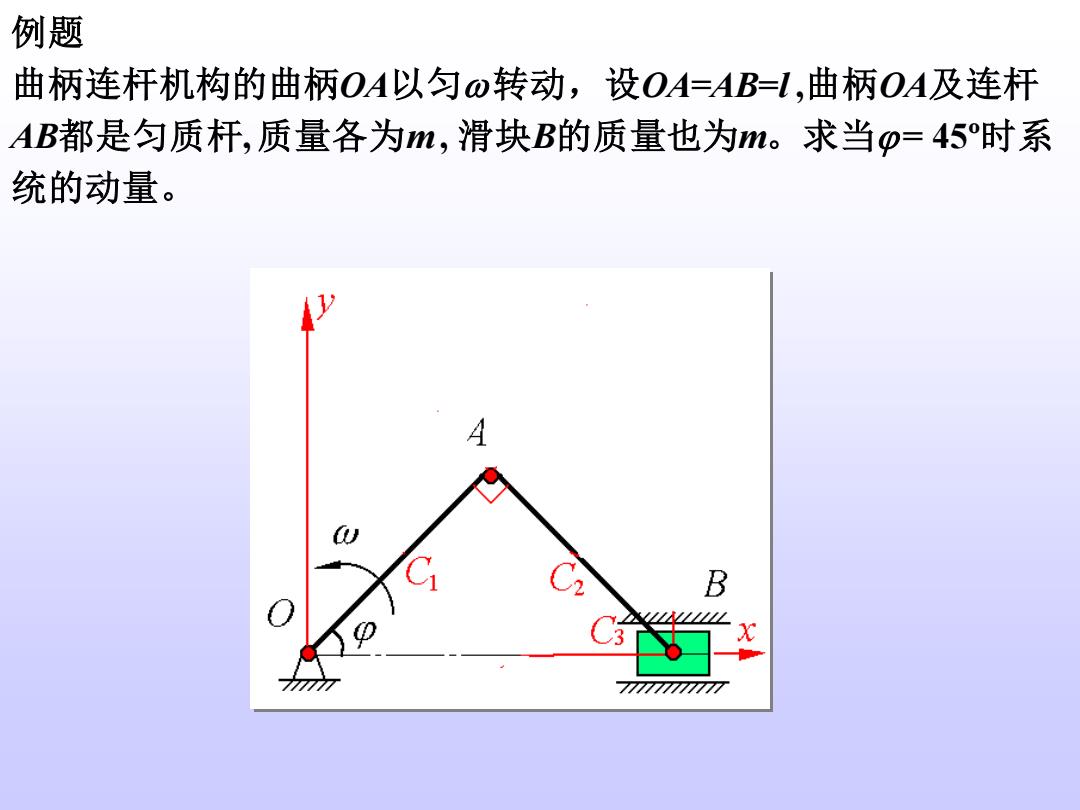
例题 曲柄连杆机构的曲柄OA以匀ω转动,设OA=AB=L,曲柄OA及连杆 AB都是匀质杆,质量各为m,滑块B的质量也为m。求当p=45时系 统的动量。 A B 3 X 777777777777
例题 曲柄连杆机构的曲柄OA以匀转动,设OA=AB=l ,曲柄OA及连杆 AB都是匀质杆, 质量各为m , 滑块B的质量也为m。求当= 45º时系 统的动量
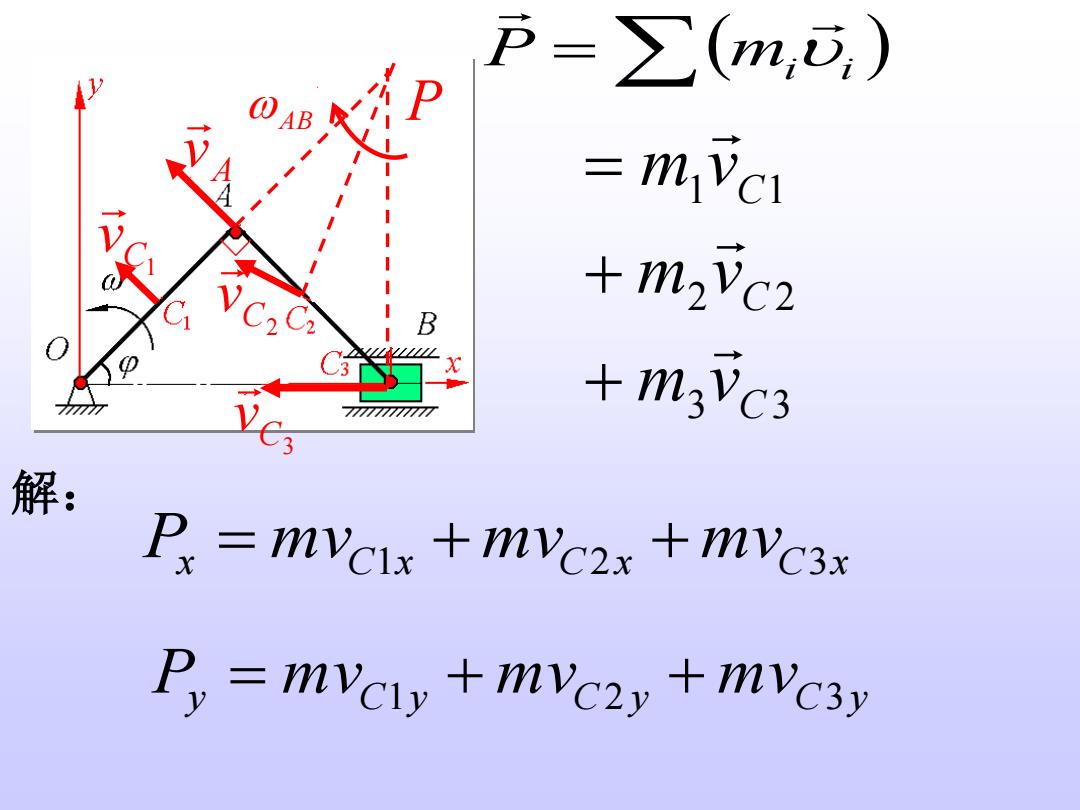
P=>(m,D) mvcr +m2c2 B 3 777777777 +m3vc3 解: P. =mvcix +mvc2x+mvc3x P,mvciy+mvc2y mvcsy
3 3 2 2 1 1 C C C m v m v m v + + = 解: Px = mvC1x + mvC2x + mvC3x Py = m vC1y + m vC2 y + m vC3y = ( ) P mi i AB P A v C3 v C1 v C2 v