
第9章刚体的平面运动 §9-3求平面图形内各点速度的瞬心法 §9-4运用分析举例
第9章 刚体的平面运动 §9-3 求平面图形内各点速度的瞬心法 §9-4 运用分析举例
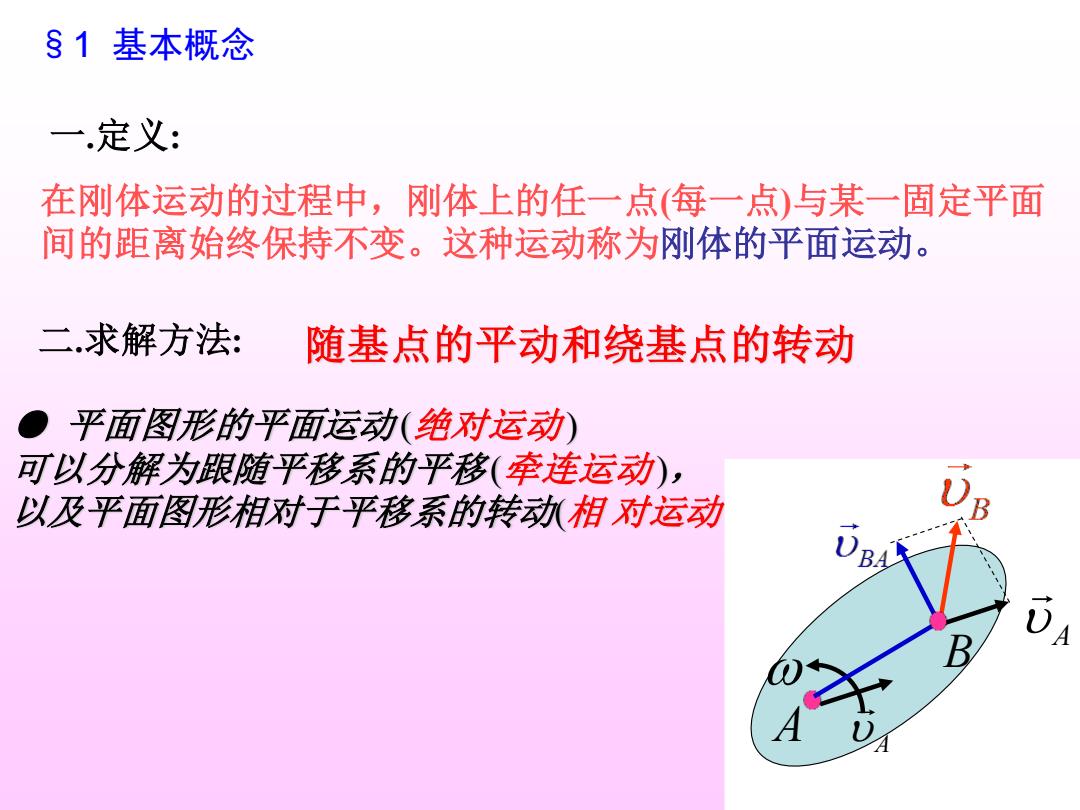
§1基本概念 一定义: 在刚体运动的过程中,刚体上的任一点(每一点)与某一固定平面 间的距离始终保持不变。这种运动称为刚体的平面运动。 二.求解方法: 随基点的平动和绕基点的转动 ● 平面图形的平面运动(绝对运动) 可以分解为跟随平移系的平移(牵连运动), 以及平面图形相对于平移系的转动相对运动
§1 基本概念 一.定义: 在刚体运动的过程中,刚体上的任一点(每一点)与某一固定平面 间的距离始终保持不变。这种运动称为刚体的平面运动。 二.求解方法: 随基点的平动和绕基点的转动 ● 平面图形的平面运动 (绝对运动) 可以分解为跟随平移系的平移(牵连运动), 以及平面图形相对于平移系的转动(相 对运动 )。 A A A B

三运动方程: X。/ =(t》 '。=y(t) p=(t) 平面运动中的转角0、角速度o、角加速度:与基点的位置无关! 四.求速度的三种方法: 一,基点法 B=下A+B4 二,投影定理 [i]。=[D]。 三,速度瞬心法 V8 Vp +VBp VBp VP 3
(xo ,,yo ,) φ φ(t) y y(t) x x(t) / / o o = = = 三.运动方程: 平面运动中的转角φ、角速度ω、角加速度ε与基点的位置无关! 二,投影定理 三, 速度瞬心法 四. 求速度的三种方法: 一 ,基点法 B A BA v v v = + B AB A AB [ ] [ ] =
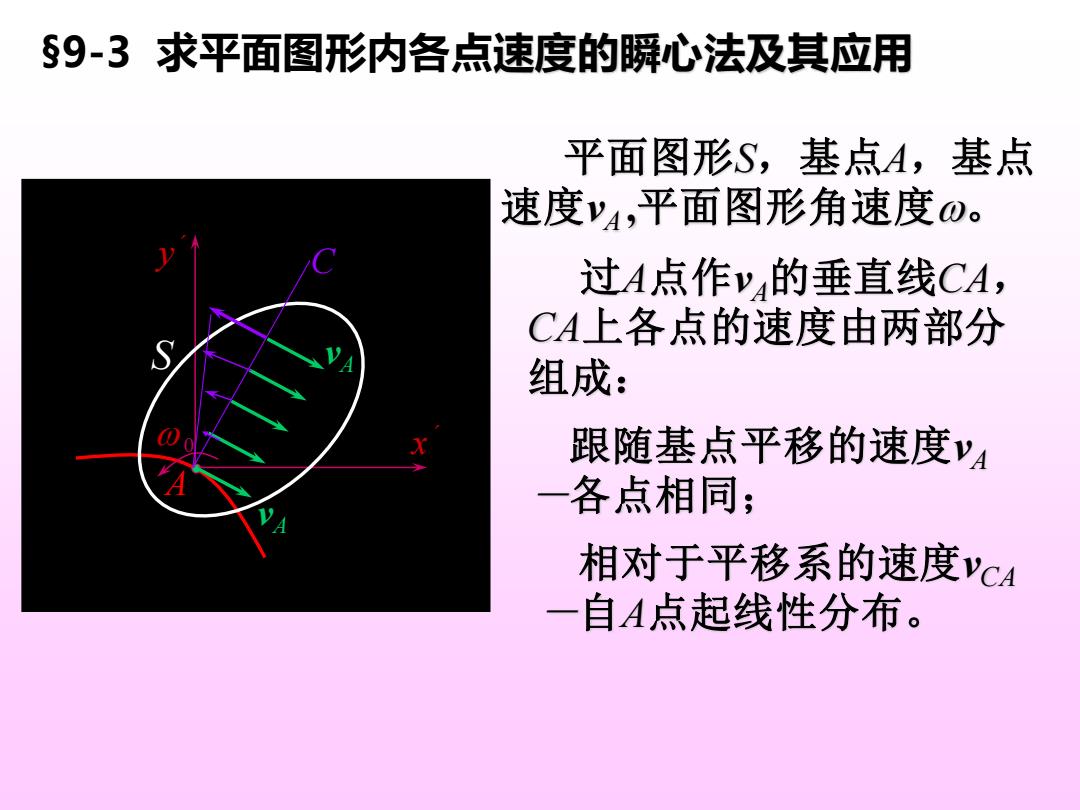
§9-3求平面图形内各点速度的瞬心法及其应用 平面图形S,基点A,基点 速度y4,平面图形角速度o。 过A点作v的垂直线CA, CA上各点的速度由两部分 组成: 跟随基点平移的速度'4 各点相同; 相对于平移系的速度'CA 一自A点起线性分布
§9-3 求平面图形内各点速度的瞬心法及其应用 0 A x ´ y ´ S C vA vA 平面图形S,基点A,基点 速度vA ,平面图形角速度。 过A点作vA的垂直线CA, CA上各点的速度由两部分 组成: 跟随基点平移的速度vA -各点相同; 相对于平移系的速度vCA -自A点起线性分布
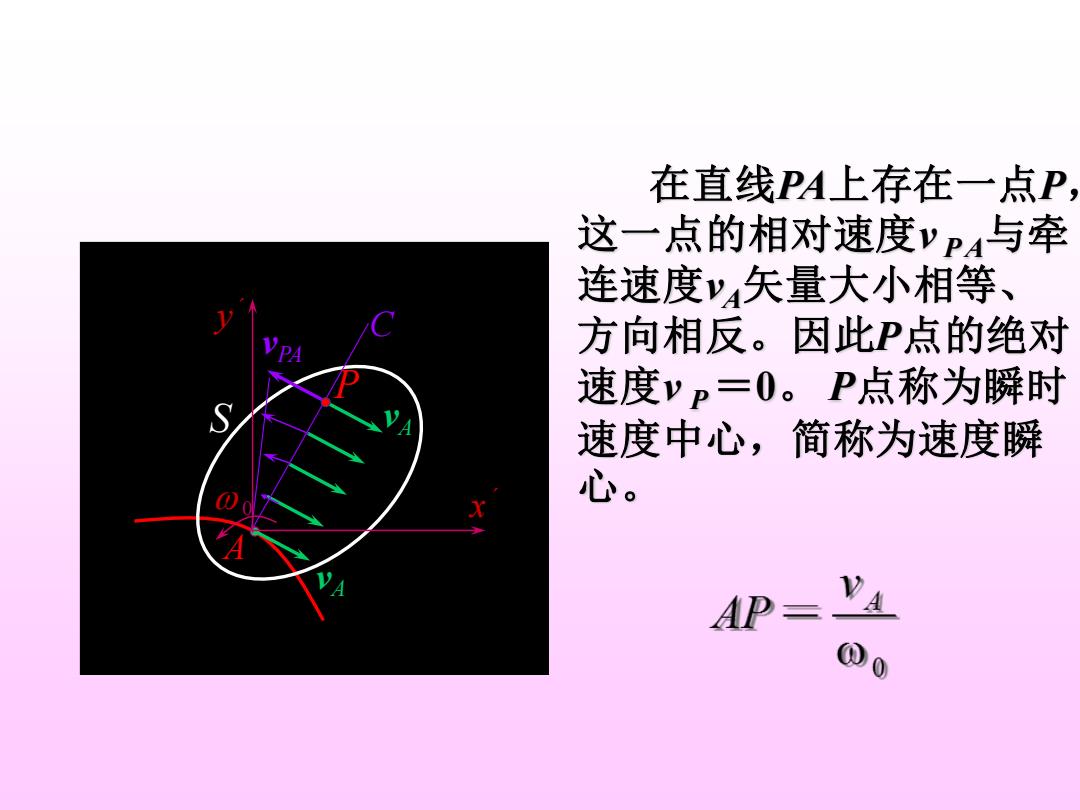
在直线PA上存在一点P 这一点的相对速度vP4与牵 连速度y4矢量大小相等 、 方向相反。因此P点的绝对 速度vp=0。P点称为瞬时 速度中心,简称为速度瞬 心。 AP= 0
0 AS C vA vA x ´ y ´ vPA P 在直线PA上存在一点 P , 这一点的相对速度v P A与牵 连速度 vA矢量大小相等、 方向相反。因此P点的绝对 速度v P = 0 。 P点称为瞬时 速度中心,简称为速度瞬 心
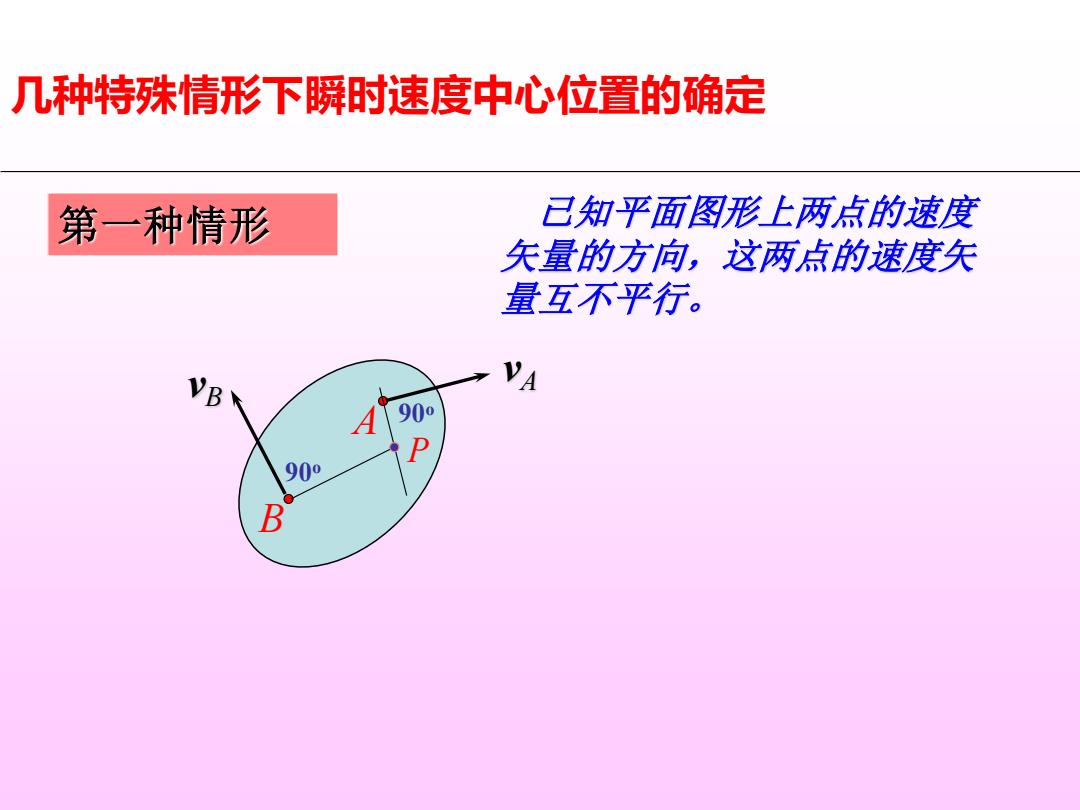
几种特殊情形下瞬时速度中心位置的确定 第一种情形 已知平面图形上两点的速度 矢量的方向,这两点的速度矢 量互不平行。 900 900 B
几种特殊情形下瞬时速度中心位置的确定 A vA B vB 90o 90o P 第一种情形 已知平面图形上两点的速度 矢量的方向,这两点的速度矢 量互不平行
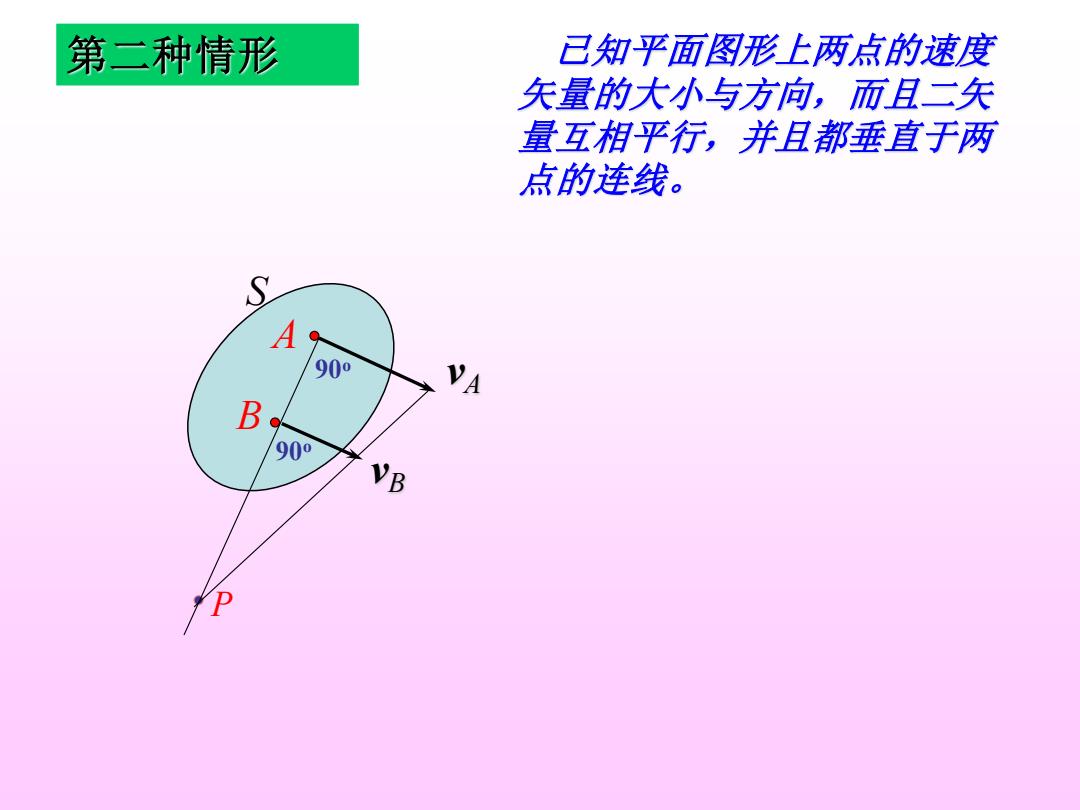
第二种情形 已知平面图形上两点的速度 矢量的大小与方向,而且二矢 量互相平行,并且都垂直于两 点的连线。 S A VA B 900 VB
S A B P 第二种情形 已知平面图形上两点的速度 矢量的大小与方向,而且二矢 量互相平行,并且都垂直于两 点的连线。 vA vB 90o 90o
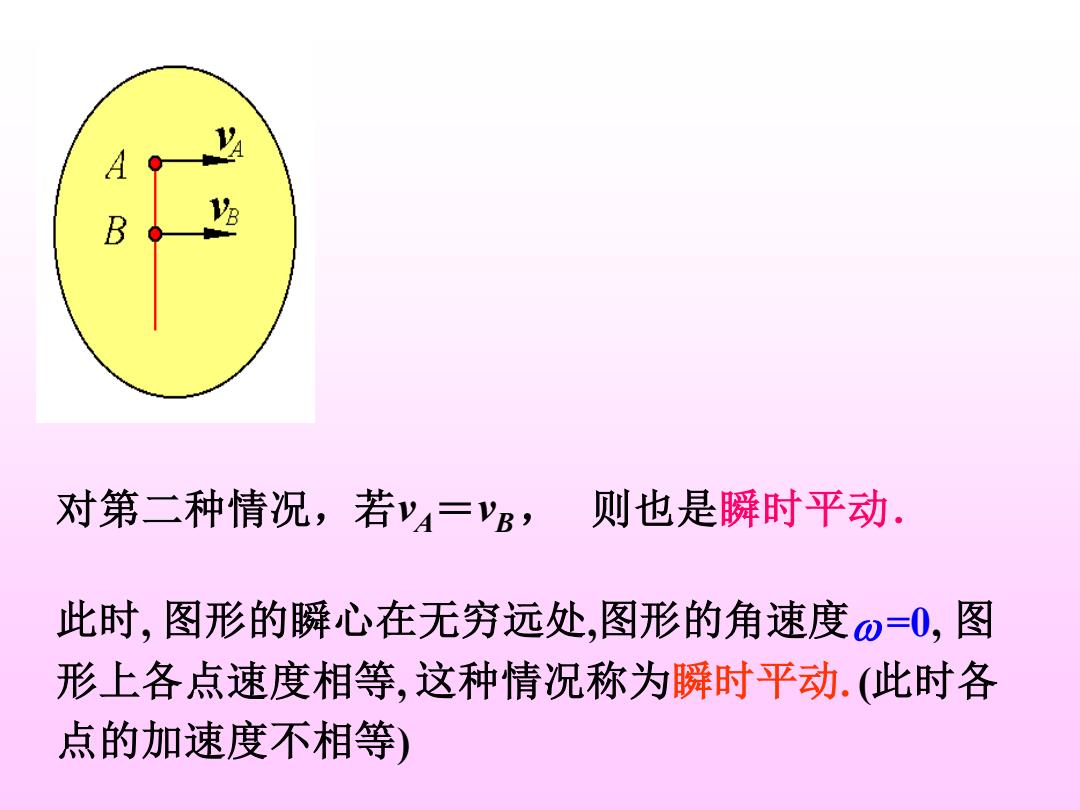
A B 对第二种情况,若v4=vB, 则也是瞬时平动. 此时,图形的瞬心在无穷远处,图形的角速度o=0,图 形上各点速度相等,这种情况称为瞬时平动.(此时各 点的加速度不相等)
此时, 图形的瞬心在无穷远处,图形的角速度=0, 图 形上各点速度相等, 这种情况称为瞬时平动. (此时各 点的加速度不相等) 对第二种情况,若vA=vB, 则也是瞬时平动.
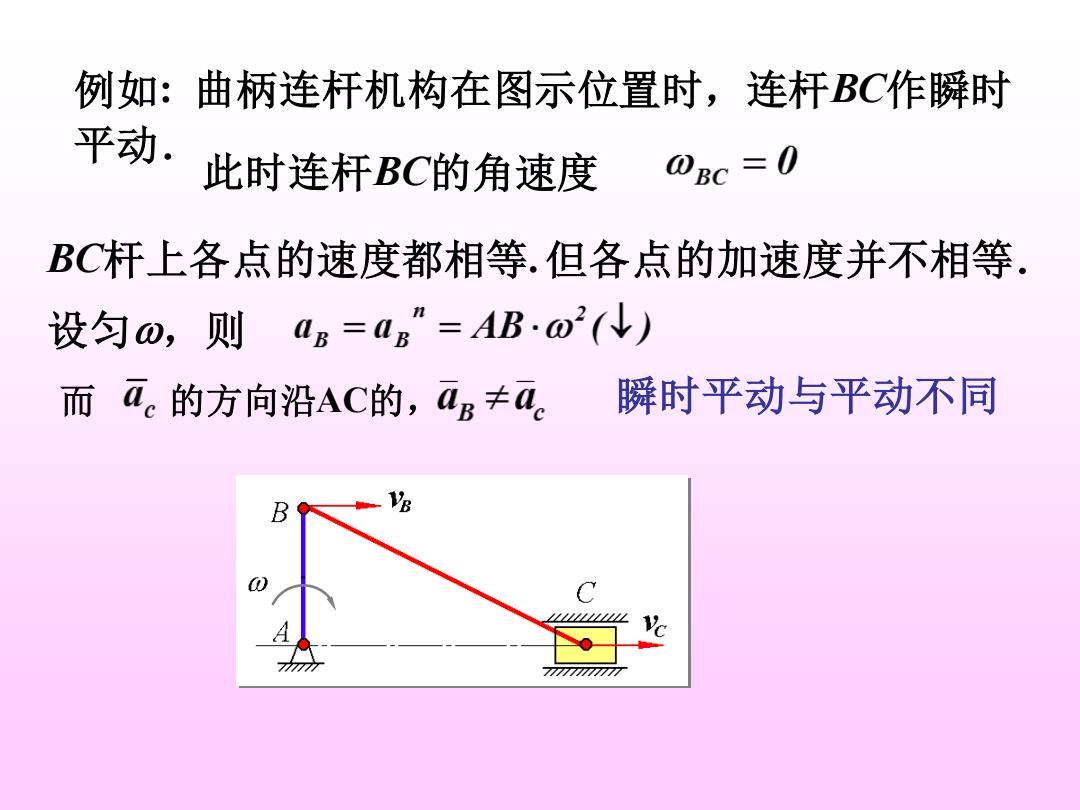
例如:曲柄连杆机构在图示位置时,连杆BC作瞬时 平动 此时连杆BC的角速度 0Bc=0 BC杆上各点的速度都相等.但各点的加速度并不相等. 设匀0,则 0B=0B”=AB02(↓) 而a。的方向沿AC的,aB≠a。 瞬时平动与平动不同 B C 7077
例如: 曲柄连杆机构在图示位置时,连杆BC作瞬时 平动.此时连杆BC的角速度 而 的方向沿AC的, BC杆上各点的速度都相等. 但各点的加速度并不相等. 设匀,则 瞬时平动与平动不同
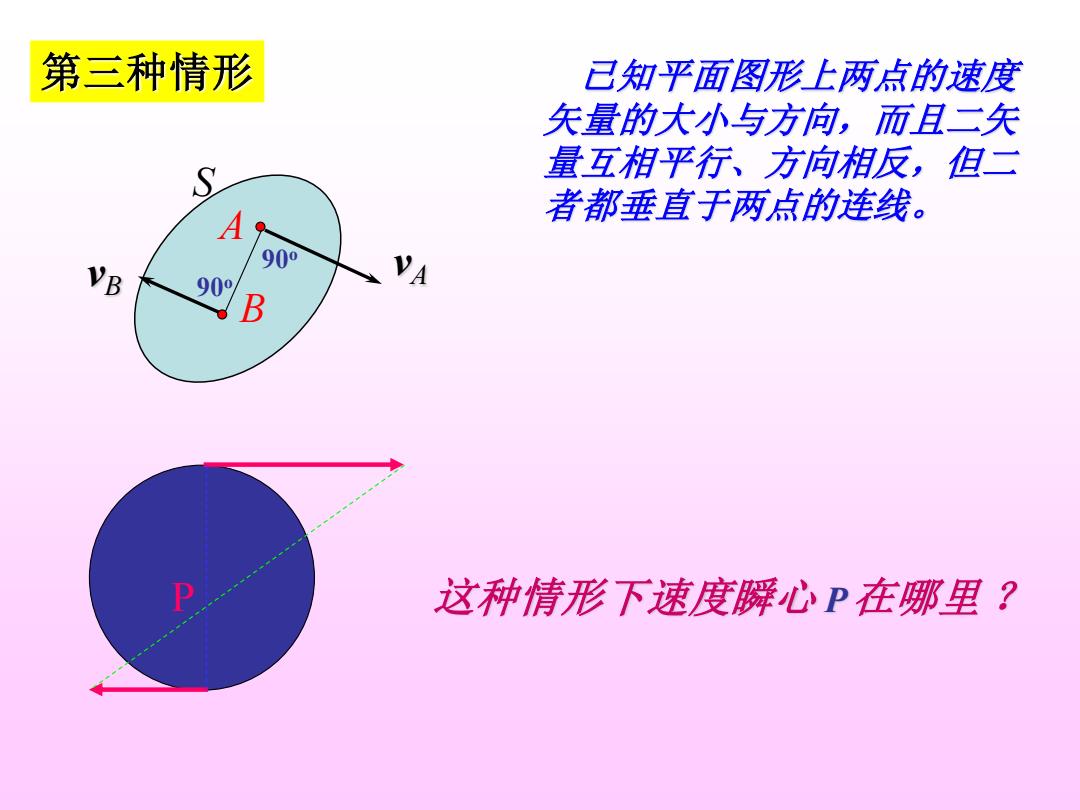
第三种情形 己知平面图形上两点的速度 矢量的大小与方向,而且二矢 S 量互相平行、方向相反,但二 A 者都垂直于两点的连线。 900 VB 90° VA B 这种情形下速度瞬心P在哪里?
S A B 第三种情形 已知平面图形上两点的速度 矢量的大小与方向,而且二矢 量互相平行、方向相反,但二 者都垂直于两点的连线。 v vA B 这种情形下速度瞬心 P在哪里 ? 90o 90o P