
佛山科学技术学院2016~2017学年第二学期 《理论力学》课程期末考试试题解答及评分标准(B) 专业、班级:土木工程系 任课教师:陈舟 一.每空0.5分,共9分 1、物体的受力分析,力学的简化,力系的平衡,物体机械运动的几何性质,运 动与力之间的关系 2、力的大小,力偶臂的长短 3、基点法,投影法,瞬心法 4、匀速直线,变速直线,匀速曲线,变速曲线 5、7,8 6、mRo 7、相等 二、(5分) AB构件3分,BC构件2分,共5分 三、(8分) 1、3分、(2)3分、(3)2分 C1 共6页第1页
佛山科学技术学院 2016 ~2017 学年第 二 学期 《理论力学》课程期末考试试题解答及评分标准 (B) 专业、班级: 土木工程系 任课教师: 陈舟 一.每空 0.5 分,共 9 分 1、物体的受力分析,力学的简化,力系的平衡,物体机械运动的几何性质,运 动与力之间的关系 2、力的大小,力偶臂的长短 3、基点法,投影法,瞬心法 4、匀速直线,变速直线,匀速曲线,变速曲线 5、7,8 6、 2 2 4 3 mR 7、相等 二、 (5 分) AB 构件 3 分,BC 构件 2 分,共 5 分 三、(8 分) 1、3 分、(2)3 分、(3)2 分 共 6 页第 1 页 O A B M C O1 VA VB c1 VC ω c2 F B A C B FB FA FB FC
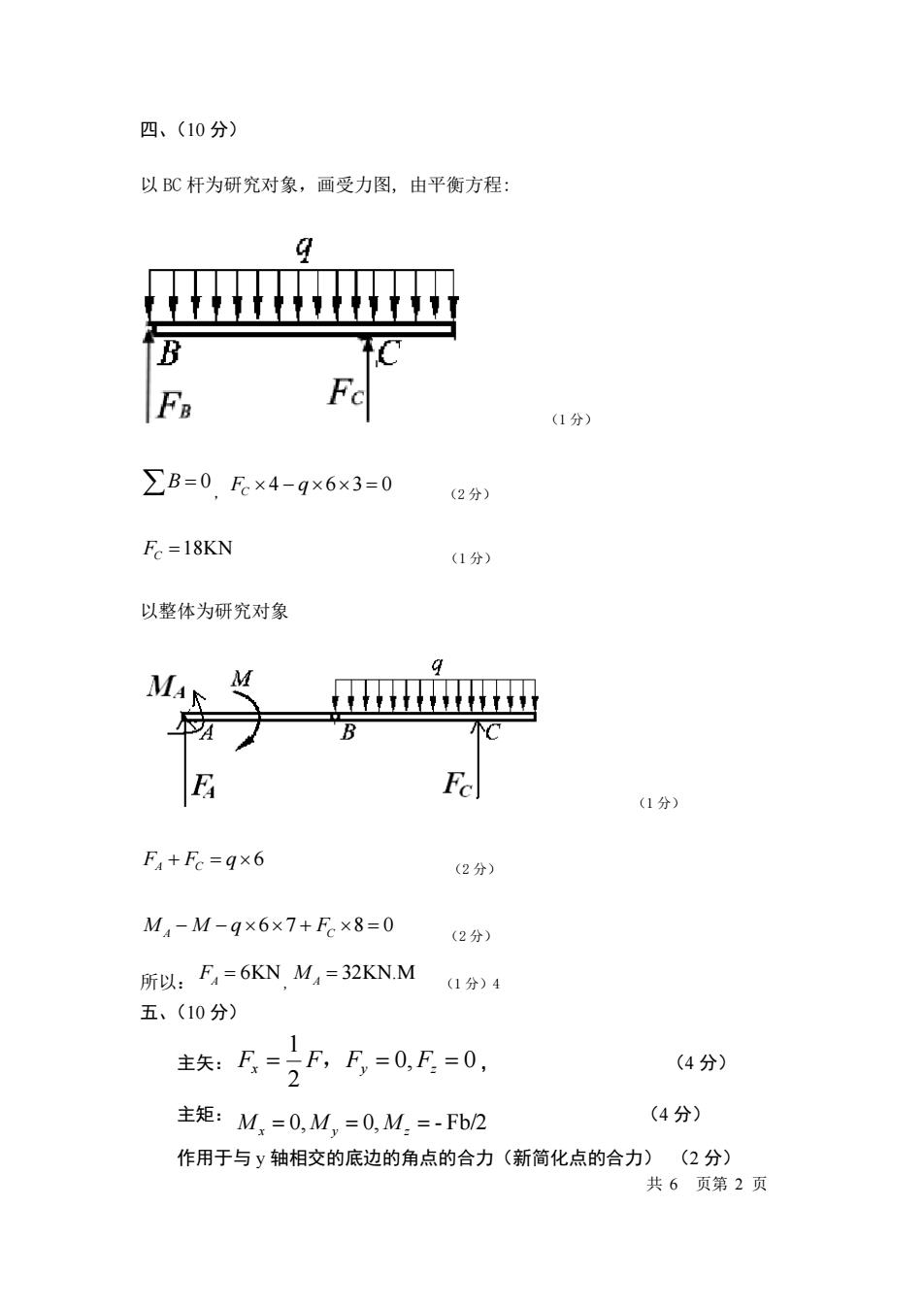
四、(10分) 以BC杆为研究对象,画受力图,由平衡方程: B (1分) ∑B=0.F×4-9x6×3=0 (2分) F=18KN (1分) 以整体为研究对象 MA 五 B Fe (1分) F4+Fc=q×6 (2分) M4-M-q×6×7+Fc×8=0 (2分) 所以:F4=6KNMA=32KNM (1分)4 五、(10分) 1 主矢:F=F,F=0,F=0, (4分) 主矩:M,=0,M,=0,M.=-Fb2 (4分) 作用于与y轴相交的底边的角点的合力(新简化点的合力)(2分) 共6页第2页
四、(10 分) 以 BC 杆为研究对象,画受力图, 由平衡方程: (1 分) B = 0 , 4 6 3 0 F q C − = (2 分) FC =18KN (1 分) 以整体为研究对象 (1 分) 6 F F q A C + = (2 分) 6 7 8 0 M M q F A C − − + = (2 分) 所以: FA = 6KN, M A = 32KN.M (1 分)4 五、(10 分) 主矢: 0, 0 2 1 Fx = F,Fy = Fz = , (4 分) 主矩: = 0, = 0, = - Fb/2 M x M y M z (4 分) 作用于与 y 轴相交的底边的角点的合力(新简化点的合力) (2 分) 共 6 页第 2 页

六、(12分) 以桁架整体为研究对象,如图,列出平衡方程: ∑F=0,Fx+F=0 (1分) ∑F=0,F+F-FE-F。=0 (2分) ∑Me(F)=0,Fe×2+F。×1-F×3-Fe×sin60×l=0 (2分) 解得: F=-5kN,Fy=7.557kN,Fp =9.44kN (1分) 选取桁架左半部分为研究对象。假定所截断的三杆都受拉力,受力如图所示,为 一平面任意力系,可列平衡方程: ∑Me(F)=0,-F×sin60'×1-F×1=0 (1分) ∑F,=0,F+E×sin60'-Fe=0 (2分) ∑M,(P)=0R×+5xsn60x1-F,x15-Fxsn60x1=0 (2分) 解得:F=-8.726kW,E=2.821kW,5=12.32kN (1分) 】 七、(10分) 元=41,y=3 (4分) x=4,少=0
六、(12 分) 以桁架整体为研究对象,如图,列出平衡方程: 0, 0 F F F x Ax F = + = (1 分) 0, 0 F F F F F y Ay By E G = + − − = (2 分) ° ( ) 0, 2 1 3 sin60 1 0 M F F F F F B E G Ay F = + − − = (2 分) 解得: 5 , 7.557 , 9.44 F kN F kN F kN Ax Ay By = − = = (1 分) 选取桁架左半部分为研究对象。假定所截断的三杆都受拉力,受力如图所示,为 一平面任意力系,可列平衡方程: ° 1 ( ) 0, sin60 1 1 0 M F F F E Ay = − − = (1 分) ° 2 0, sin60 0 F F F F y Ay E = + − = (2 分) ° ° 3 1 ( ) 0, sin60 1 1.5 sin60 1 0 2 M F F F F F D E Ay Ax = + − − = (2 分) 解得: 1 2 3 F kN F kN F kN = − = = 8.726 , 2.821 , 12.32 (1 分) 七、(10 分) 4 , 3 4, 0 x t y x y = = = = (4 分)
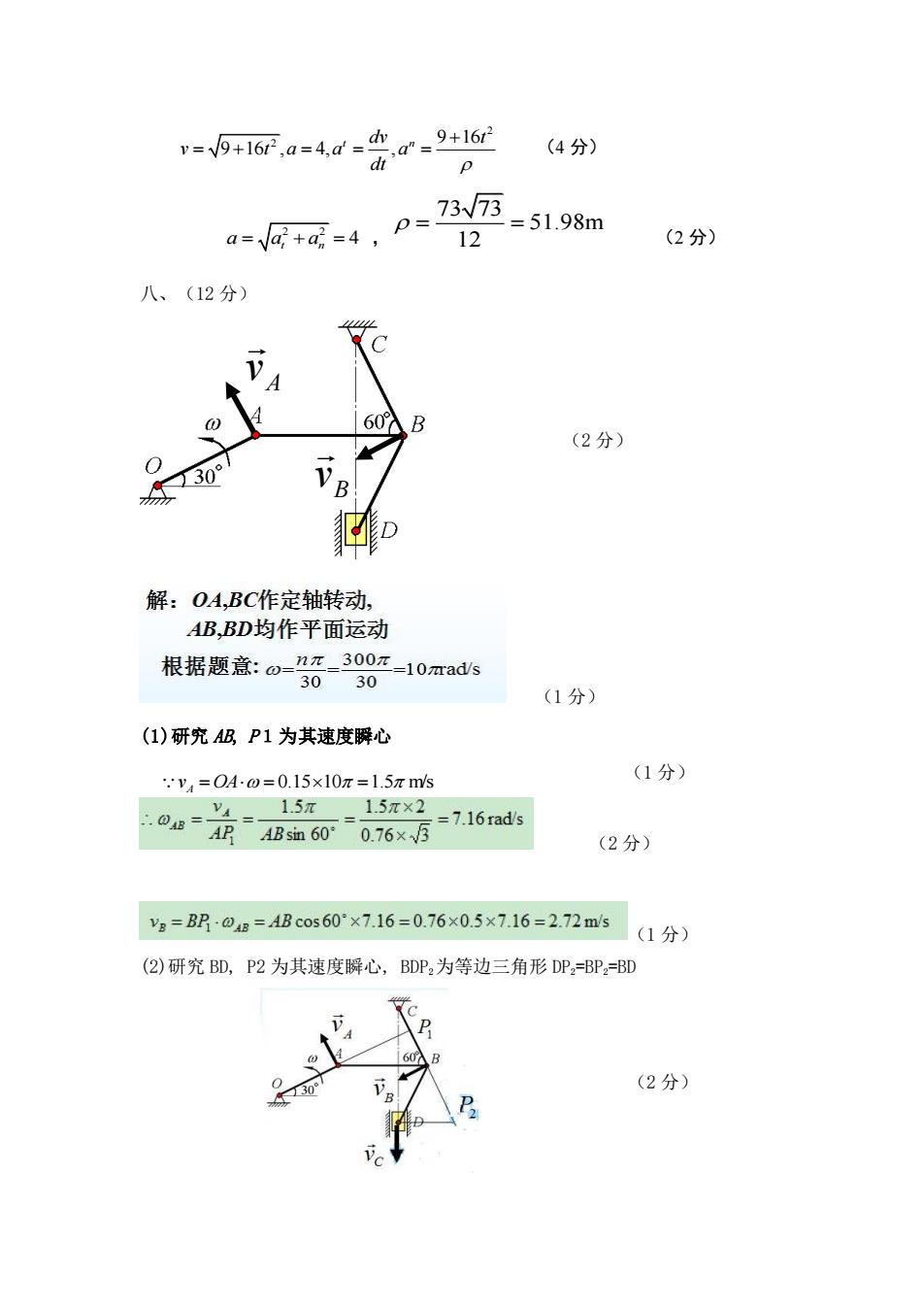
=51a=4d-价c94 (4分) a+-4,p-73y 12 =51.98m (2分) 八、(12分) 60入 B (2分) 230° ☑D 解:OA,BC作定轴转动, AB,BD均作平面运动 根据题意:o-n元-300r-10mads 30 30 (1分) (1)研究ABP1为其速度瞬心 v4=OA0=0.15×10π=1.5πm/s (1分) 1.5π 1.5π×2 04B= VA AP =7.16rad/s ABsin 60* 0.76×5 (2分) Vg=B308=AB cos60°×7.16=0.76×0.5×7.16=2.72ms (1分) (2)研究BD,P2为其速度瞬心,BDP2为等边三角形DP2=BP2=BD (2分)
2 2 9 16 9 16 , 4, , t n dv t v t a a a dt + = + = = = (4 分) 2 2 a a a = + = t n 4 , 73 73 51.98m 12 = = (2 分) 八、(12 分) A v B v (2 分) (1 分) (1)研究 AB, P1为其速度瞬心 (1 分) (2 分) (1 分) (2)研究 BD, P2 为其速度瞬心, BDP2为等边三角形 DP2=BP2=BD (2 分) v = OA = 0.1510 =1.5 m/s A

共6页第4页 VB BP@4B =2.72 m/s (1分) 00==2.73 BP =5.13rad/s 0.53 (1分) Yo=D30p=0.53×5.13=2.72ms( (1分) 九、(12分) 解:物体受力和运动分析如图所示 y (2分) p=mv.=mol (1分) 4 L.-Jw-3mlo (1分) T=2mPo (1分) 3 ac.=-ac sino-ac coso =-la sino lo2 coso acy =-ac coso +ac sino =-la coso+lo'sin -ml(a sin+acosp)=Fo -ml(a coso-w'sin )For -mg (5分) Fo:=-ml(a sino+o'coso) Fo,mg -ml(a coso-o'sino) 解得: (2分) 十、(12分)
共 6 页第 4 页 (1 分) (1 分) (1 分) 九、(12 分) 解:物体受力和运动分析如图所示 (2 分) c p mv m l = = (1 分) 4 2 3 L J w ml z z = = (1 分) 2 2 2 3 T ml = (1 分) (5 分) 解得: (2 分) 十、(12 分) 2.72m/s vB = BP1 AB =

(2分) 共6页第5页 I1=0 1卫 (2分) 而yg=yp+R0B=RO4+R0g (1分) 确定OA与OB的关系,为此,分别研究A、B轮,受力分别如图所示,对A轮应用定轴转 动微分方程: JE=M=TR (1分) 对B轮应用相对于质心的动量矩定理: JgE8 =Ma=TR (1分) .EA=EB 由于系统初始静止,将上式积分后有: 04=0g Vg =2R@8 (1分) 5P T= 8g 8 (2分) W=Ph .VB=1 2)上式两端对时间求导后有: (2分) aa=58 共6页第6页
(2 分) 共 6 页第 5 页 (2 分) (1 分) 确定 ωA 与 ωB的关系,为此,分别研究 A、B 轮,受力分别如图所示,对 A 轮应用定轴转 动微分方程: (1 分) (1 分) 由于系统初始静止,将上式积分后有: (1 分) (2 分) (2 分) 共 6 页第 6 页