
佛山科学技术学院2017~2018学年第二学期 《理论力学》课程期末考试试题解答及评分标准(C) 专业、班级:土木工程系任课教师:罗冬梅、陈舟、王英涛 一.选择题,每题2分,共10分 1、C,2、C,3、A,4、C,5、D 二、(1)解:向点0简化 F=55-万-E=-150N 2 F=万5-B=0 所以F=-150N(3分) Mo=F×30+E×50-F×30-M =80×30+40×50-110×30-2000(3分) =-900Nmm 合力大小FR=150N,方向水平向左。合力作用线方程为: 1=%0 1FR150 -6mm 由Mo转向知合力作用线方程为:y=-6mm。(3分) (2)解:向点0简化, F.=-5.5.-1N 2 F=1+5.5=2N F=-3N 所以F(i+2-3k)N,F=√FR+F房+F是=4N(4分) M,--(xxI+3xI)a=-4aNom 以-(6x1-5x2xu=2aNn 共5页第1页
佛山科学技术学院 2017~2018 学年第 二 学期 《理论力学》课程期末考试试题解答及评分标准 (C) 专业、班级: 土木工程系 任课教师:罗冬梅、陈舟、王英涛 一.选择题,每题 2 分,共 10 分 1、C, 2、C, 3、A,4、C, 5、D 二、(1)解:向点 O 简化 ' 1 2 4 2 150N 2 F F F F Rx = − − = − ' y 1 3 2 0 2 F F F R = − = 所以 ' FR =-150N (3 分) 2 3 4 30 50 30 80 30 40 50 110 30 2000 900N mm M F F F M O = + − − = + − − = − (3 分) 合力大小 FR=150N,方向水平向左。合力作用线方程为: O R 900 6mm 150 M y F = = = 由 MO 转向知合力作用线方程为:y=-6mm。(3 分) (2)解:向点 O 简化, 2 - 2 1N 2 FRx = = − y 2 1 2 2N 2 FR = + = z FR = −3N 所以 FR =(-i+2j-3k)N, 2 2 2 F F F F R Rx Ry Rz = = 14N + + (4 分) 2 ( 2 1 3 1) 4 N m 2 M a a x = − + = − 2 (3 1 2 1) 2 N m 2 M a a y = − = 共 5 页第 1 页

M.=(lx1+xxla=2aNom 所以M=(-4ai+2ag+2ak)Nm,M=√M+M+M=√24aNm(5分) 三、 M 0.5 F py 0.51 Dx (b) (a 解1.以杆DC为对象,受力如图(b) ∑Mc=0,Fm1-F.0.51=0 ·Fm=2F=10kN (3分) 2.以局部整体BCD为对象,受力如图(c) ∑M。=0,F1+F21-E1+M=0 66-当留-号9 =-2.5kN(4分) 3.以整体为对象,受力如图图(a) 1 ∑F=0,Fa+59l+F-E=0 F。=r-59l-=20-82-10=2w ∑E,=0,F+F=0 .Fy =-FDy =2.5 kN (4分) ∑M,=0M,90+M++21=0 M,-9-M-fW-2/=g82-10-202-225)2=-1467Nm4分) 共5页第2页
z 2 (1 1 2 1) 2 N m 2 M a a = + = 所以 M ai aj ak = + + (-4 2 2 )N m , 222 M M M M a = + + x y z = 24 N m (5 分) 三、 解 1. 以杆 DC 为对象,受力如图(b) 0, 0.5 0 1 10kN 2 C Dx Dx P M F l F l F F = − = = = (3 分) 2. 以局部整体 BCD 为对象,受力如图(c) 1 0, 2 0 2 1 1 20 10 10 2.5 kN 4 2 2 4 2 2 2 B Dx Dy P Dy P Dx M F l F l F l M M F F F l = + − + = = − − = − − = − (4 分) 3. 以整体为对象,受力如图图(a) ( ) 2 2 1 0, 0 2 1 1 20 8 2 10 2 kN 2 2 0, 0 2.5 kN 1 1 1 0, 2 0 2 3 2 1 1 1 1 2 8 2 10 20 2 2 2.5 2 14.67 kNm 6 2 4 6 4 2 x Ax Dx P Ax P Dx y Ay Dy Ay Dy A A P Dy A P Dy F F ql F F F F ql F F F F F F M M ql l M F l F l M ql M F l F l = + + − = = − − = − − = = + = = − = = − + + + = = − − − = − − − − = − ( 分) ( 分) 共 5 页第 2 页 q A D FP l l l M 0.5l 0.5l D B C F C FDx FDy FCy FCx M B C FBx FBy (a) (b) (c) FDx FDy FAy FAx M A D FP FDx FDy

四、解:设AB=BC=l,杆AB和杆BC的质量为m,AB与BC的夹 角为0。 以整体为研究对象,可知: ∑M4=0 1o=0 Fy21-sin -2mgcos mg 2 2 2 =受4cor号 mg (4分) FN F 以BC为研究对象,可知:∑Mg=0 F4hsn号mgr7eosg-f4heo 2 2 2 00 mg F,≤Fw=0.5Fw 解得:cot号≥4,所以0<2arcc0t4(5分) 五、 解以OA杆上的A点为动点,凸轮为动系 Va=ve+V ..v=v.cot vo cot y,=v。/sinp=vo/sinp R ..@B=v/AB=vo coto/(2R)(5) 77 又G+dg=a.+d,+d+ae(a) 其中 a a.=0,a=vicot2/(2R), A (4分) B a=v2/R=v/(Rsin2p).ac=0 式(a在n方向上投影: -a'sing-a"cosp a" -a.cotcot'o/(2R) sino Rsin'o (5分) 6-(2+c0s2p) ÷a4B=d1AB=4R'simp 代入数据,得 √5wo 哈17 OAB= (2分) 6R OAB=- R212V5 共5页第3页
四、解:设 AB=BC=l,杆 AB 和杆 BC 的质量为 m,AB 与 BC 的夹 角为 θ。 以整体为研究对象,可知: 0 MA = 2 sin 2 cos 0 2 2 2 N l F l mg − = ∴ = cot 2 2 N mg F (4 分) 以 BC 为研究对象,可知: B M = 0 sin + cos - cos 0 2 2 2 2 N f l F l mg F l = 0.5 F fF F f N N = 解得: cot 4 2 ,所以 2arccot 4 (5 分) 五、 ( ) ( ) 2 0 2 3 3 0 2 0 3 2 3 cot cot / 2 sin sin / 2 cos 4 sin n t n r a a t AB a a v a a v R R v a AB R = − − = − − = = − + (5 分) 代入数据,得 2 0 0 2 3 17 6 12 3 AB AB v v R R = = − (2 分) 共 5 页第 3 页 解 以 OA 杆上的 A 点为动点,凸轮为动系 ( ) 0 0 0 cot cot / sin / sin / co / t 2 5 a e r a e r e AB a v v v v v v v AB v R = + = = = = = = ( 分) v v v 又 ( ) t n t n a a e r r C a a a a a a + = + + + a 其中 ( ) ( ) 2 2 0 2 2 2 0 0, cot / 2 , / / sin , 0 n e a n r r C a a v R a v R v R a = = = = = (4 分) 式 (a) 在 方向上投影: sin cos a a t n n r − − = a a a C A FAx FAy FN Ff mg mg C FN Ff B FBy FBx mg A B t a a n a t a r a n r a R A B 0 v e v r v a v
六、解 77777 1AB作平面运动,瞬心在O,所以 04B= va u h u=8(m/s) Ya=sine=sing- (4分) 2BC作平面运动,由速度投影定理 Va COs B=vccos ..vc=va cos(90--0)/cos=82cos15 ( 0,==8V2cos15 =273.16 0.04 七、解:(1)质心的速度为:v= 6 杆AB的动量为p=m=mLw (3分) 6 (2)对0点的转动惯量o-古mt+m哈-d 杆AB的动量矩为L=Jow= gmL(3分) (3)杆AB的动能为 T=Jow2=及m2亚3分) 18 八、解:以整体为研究对象,画出系统的主动力如下: m2,T2 1713g m g 17 13g 根据各部分的运动形式,写出系统初始和末了的动能T1和T2, 共5页第4页
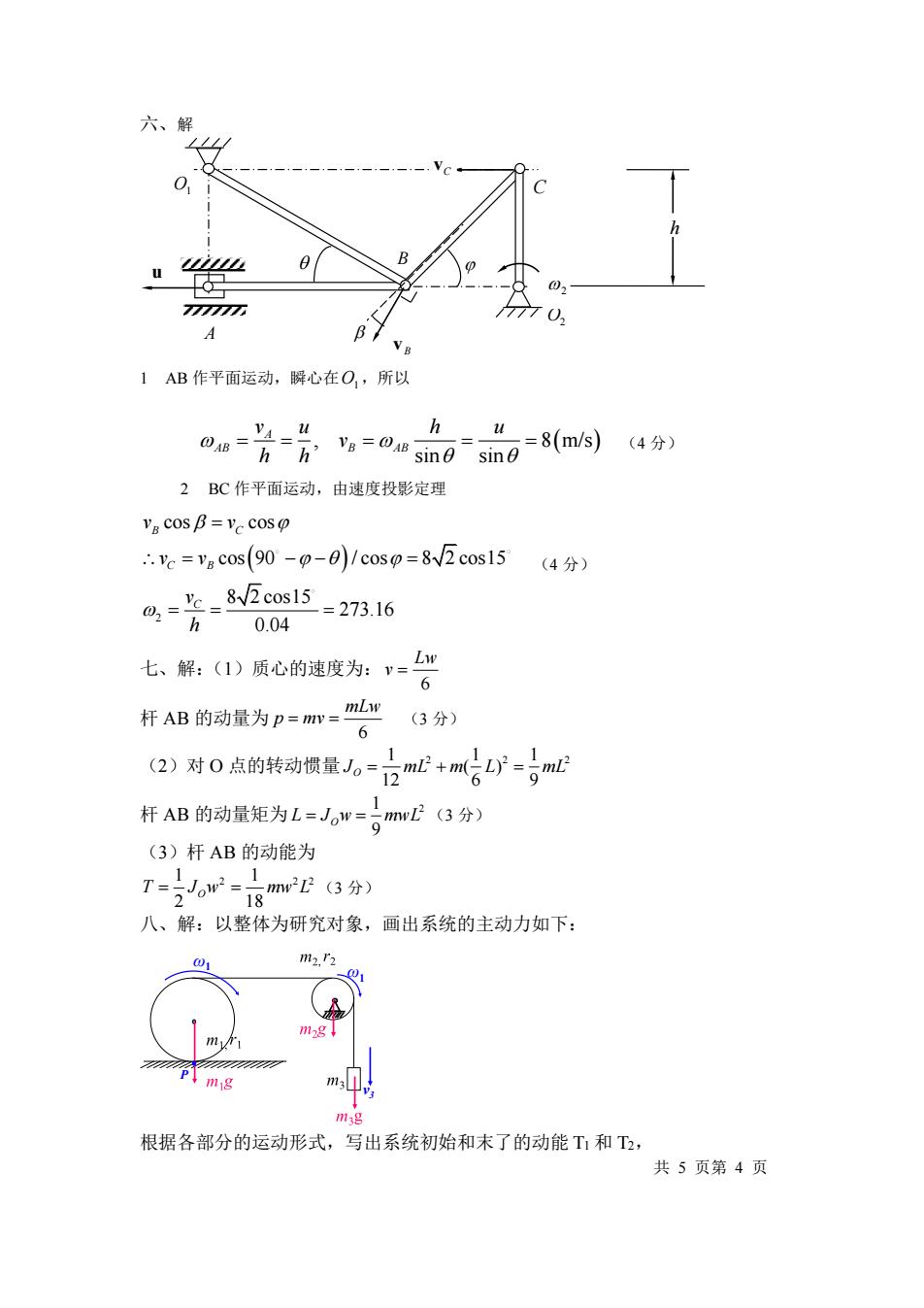
六、解 1 AB 作平面运动,瞬心在 O1 ,所以 , 8 m/s ( ) sin sin A AB B AB v u h u v h h = = = = = (4 分) 2 BC 作平面运动,由速度投影定理 ( ) 2 cos cos cos 90 / cos 8 2 cos15 8 2 cos15 273.16 0.04 B C C B C v v v v v h = = − − = = = = (4 分) 七、解:(1)质心的速度为: 6 Lw v = 杆 AB 的动量为 6 mLw p mv = = (3 分) (2)对 O 点的转动惯量 1 1 1 2 2 2 ( ) 12 6 9 O J mL m L mL = + = 杆 AB 的动量矩为 1 2 9 L J w mwL = = O (3 分) (3)杆 AB 的动能为 1 1 2 2 2 2 18 T J w mw L = = O (3 分) 八、解:以整体为研究对象,画出系统的主动力如下: P ω1 ω1 v3 根据各部分的运动形式,写出系统初始和末了的动能 T1 和 T2, 共 5 页第 4 页 u O1 O2 B C A h B v C v 2

系统初始静止,工=0 2y=2r01=502=3 (1分) 1 s11 (3分) 2 网+2+aK 计算系统在整个运动过程中所有力所作的功,W=m,gh (2分) 由动能定理知:T-T=W .[弓m+2m2+4mr@=m8h 即)弓m+2m+4m,=m动,3 2mgh 3 m1+2m2+4m 2 两边对时间求导,可得:4,= 2m38 (4分) 3 2m+2m,+4m, 以m3为研究对象, m3的加速度为a=2a,= 4m38 3 (2分) 三m,+2m2+4m 根据质心的运动定理知: mg-T ma (m +2mz)m38 ∴.T=m38-m343= 3 (3分) 2m+2m+4m, 共5页第5页
系统初始静止, 1 T = 0 1 1 1 2 2 3 2 2 v r r v = = = (1 分) 1 1 2 2 2 2 2 1 2 3 3 2 2 2 2 2 2 1 1 1 1 1 2 3 1 1 2 2 1 2 3 1 1 111 222 1 1 1 1 1 2 = ( ) ( )( ) (2 ) 2 2 2 2 2 1 3 = [ 2 4 ]( ) 2 2 T J J m v P B r m r m r m r m r r m m m r = + + + + + + + (3 分) 计算系统在整个运动过程中所有力所作的功, W m gh = 3 (2 分) 由动能定理知: T T W 2 1 − = ∴ 2 1 2 3 1 1 3 1 3[ 2 4 ]( ) = 2 2 m m m r m gh + + 即 2 1 2 3 1 3 1 3[ 2 4 ] = 2 2 m m m v m gh + + , 2 3 1 1 2 3 2 = 3 2 4 2 m gh v m m m + + 两边对时间求导,可得: 3 1 1 2 3 2 = 3 2 4 2 m g a m m m + + (4 分) 以 m3 为研究对象, m3 的加速度为 3 3 1 1 2 3 4 =2 = 3 2 4 2 m g a a m m m + + (2 分) 根据质心的运动定理知: m g T m a 3 3 3 − = ∴ 1 2 3 3 3 3 1 2 3 3 ( 2 ) 2 = 3 2 4 2 m m m g T m g m a m m m + = − + + (3 分) 共 5 页第 5 页