
佛山科学技术学院20~20 学年第 学期 《理论力学》课程期考试试题解答及评分标准(D) 专业、班级: 任课教师: 一.填空题(每空1分,共10分) )2518(2)100,(3)54)56,- Fb,0 3 3 (5)mRw,mRw 3 mR'w2 (2分) (3分) (3分) 三、解:设木箱将要滑动时拉力为F1 ∑F=0Fmx-Ecos0=0 2F,=0F,-P+fsi加003分) Fnx=fFN F= fp cos0+f sine -=1876N(2分) 设木箱有翻动趋势时拉力为F2
佛山科学技术学院 20 ~20 学年第 学期 《理论力学》课程期 考试试题解答及评分标准 (D) 专业、班级: 任课教师: 一.填空题(每空 1 分,共 10 分) (1) 2 13,18 ,(2)100N,(3)5 (4) 3 Fb 3 , 3 Fb 3 − ,0 (5) mRw, 2 mR w, 3 2 2 4 mR w 二. (2 分) (3 分) (3 分) 三、解:设木箱将要滑动时拉力为F1 (3 分) F f F max = s N 1 1876 cos sin s s f F f = = + N (2 分) 设木箱有翻动趋势时拉力为F2

M =0F.cos0.h-p.a=0 Pa=1443N(3分) F:=2hcos0 能保持木箱平衡的最大拉力为1443N,拉力为1kN时平衡。(2分) 四、(共12分)解: Fex 个600 60 A D MA 城 F (DBC杆及系统的受力图各2分) 解:先以直角杆CED为研究对象,分析受力。 ∑McF)-0, RwED-Pcos60°.CE=0 FD×2-20c0s60°×2=0 o=10(k) 再以整体为研究对象,受力分析如图,根据平衡方程: ∑X-0,F,-Pcos60°=0 (3分) Σy0,Pw+Fw-gBC-Pm60°=0 ∑MF)0,MA+DAD-Psm60°.AE=0 (2分)
0 = MA 2 cos 0 2 a F h P − = 2 1443 2 cos Pa F h = = N (3 分) 能保持木箱平衡的最大拉力为 1443N,拉力为 1kN 时平衡。(2 分) 四、(共 12 分) 解: (3 分) (2 分)

共5页第2页 解得: F=10(k) (答案1分) F0=14+10W3=31.32(k0 (答案1分) MA=203-40=-5.36kN.m) (答案1分) 五、(共10分)解:DE杆为零力杆 (3分) ∑M,(F)=0:Fl+F1sn60°=0 (3分) Foo--3r (2分) 2 (2分) 六、(共12分) 解: 动量:px=2awm/2,py=awm/6 动量矩:a2wm 动能:a2w2m/2 七、(共12分)解: AB作平面运动,瞬心为C(2分)
共 5 页第 2 页 五、(共 10 分)解: DE 杆为零力杆 (3 分) ( ) = 0: + sin 60 = 0 o MA F FCDl Fl (3 分) FCD F 2 3 = − (2 分) FCF F 2 1 = (2 分) 六、(共 12 分) 解: 动量:px=2awm/2,py=awm/6 动量矩:a 2wm 动能:a 2w2m/2 七、(共 12 分)解: AB 作平面运动,瞬心为 C (2 分)

2选D为基点,4D=1w2 分别沿5轴和n轴投影 a cosp=ap cos(-20)-ap 0=-apsin p+ap cosp+aasin (10) 解得a4=-1o2 aD=0 QAB= d'D= AD 八、(14分) Q8-ON=OA 2r 2 解: (1分) 11 22 r2.0+ 2网R2.号=2mr2明 13 系统此时的动能为 22 4 4.4.4一 (2分) 7 r20月-T6=Me 根据动能定理, 万-T6=Mp有 4 (2分) 两边同时对时间求导数,得 mragBA-Mo 24M A= 解得 72 (求出得2分)》 共5页第4页
(10 分) 八、(14 分) 解: (1 分) (2 分) (2 分) 共 5 页第 4 页
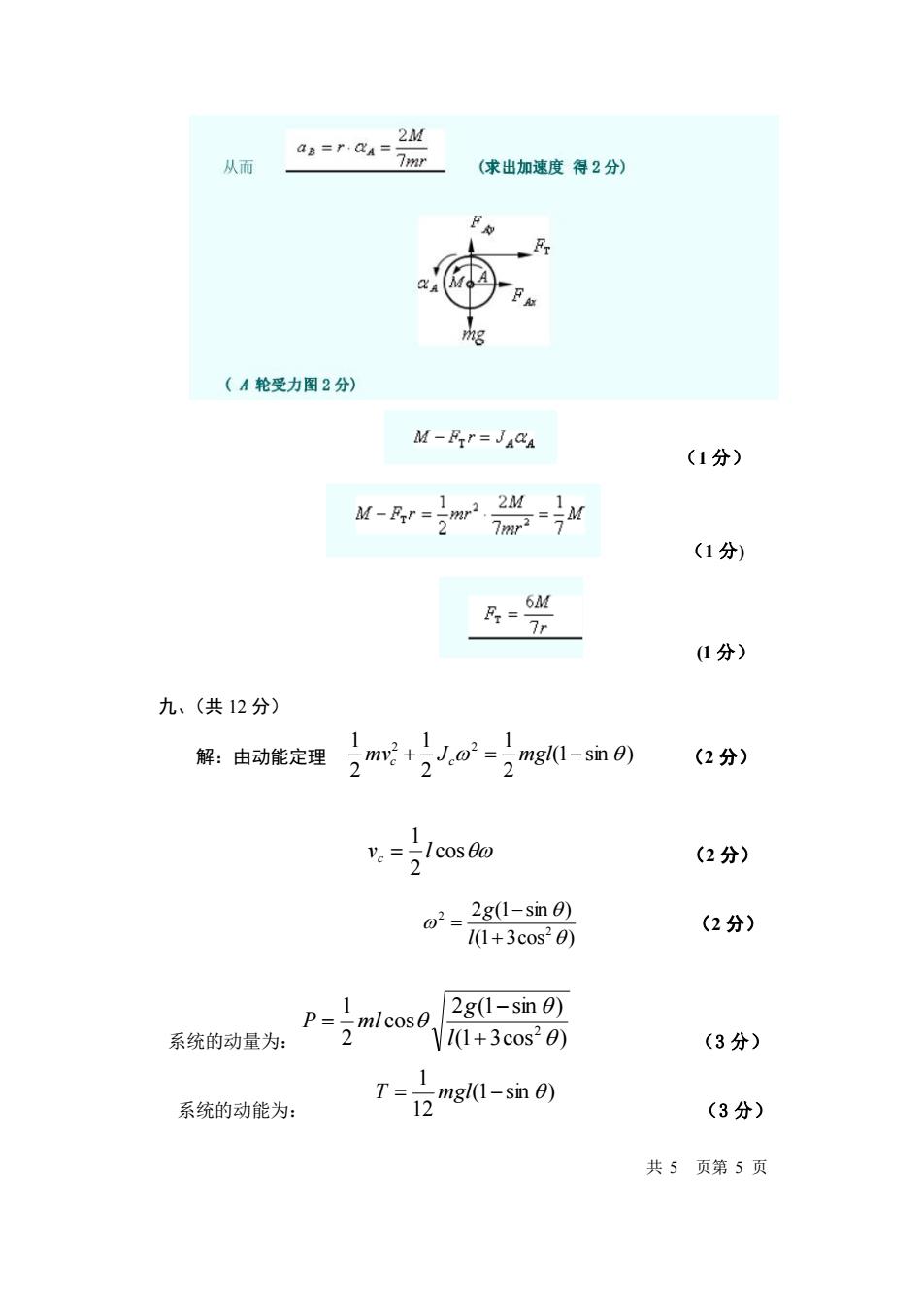
2M aB=r.aA= 从而 7mr (求出加速度得2分) mg (A轮受力图2分) M-Fr=JAaA (1分) (1分) F= 6M (1分) 九、(共12分) 1 解:由动能定理 2m2+ >②2三1(1-sm©) (2分) Ve=Icos0@ (2分) 02= 2g(1-sin0) 11+3cos20) (2分) 1 P= nlcos0 2g(1-sin0) 系统的动量为: 2 11+3cos20) (3分) T= mgl(1-sin 0) 系统的动能为: 1 (3分) 共5页第5页
(1 分) (1 分) (1 分) 九、(共 12 分) 解:由动能定理 (1 sin ) 2 1 2 1 2 1 2 2 mvc + Jc = mgl − (2 分) cos 2 1 v l c = (2 分) (1 3cos ) 2 (1 sin ) 2 2 + − = l g (2 分) 系统的动量为: (1 3cos ) 2 (1 sin ) cos 2 1 2 + − = l g P ml (3 分) 系统的动能为: (1 sin ) 12 1 T = mgl − (3 分) 共 5 页第 5 页
