
第9章刚体的平面运动 §9-1 刚体的平面运动及其分解 §9-2 平面图形上任意点速度的求法
第9章 刚体的平面运动 §9-1 刚体的平面运动及其分解 §9-2 平面图形上任意点速度的求法
latil r A B ① B
O u B r θ φ ω θ CB O A
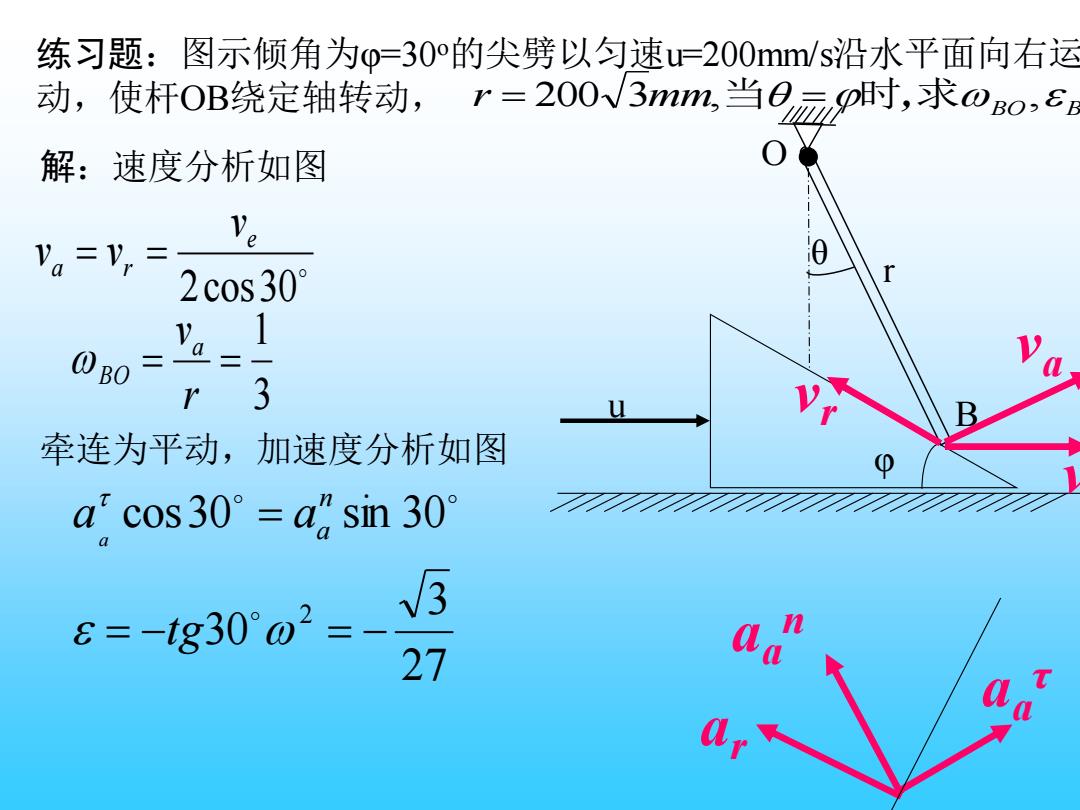
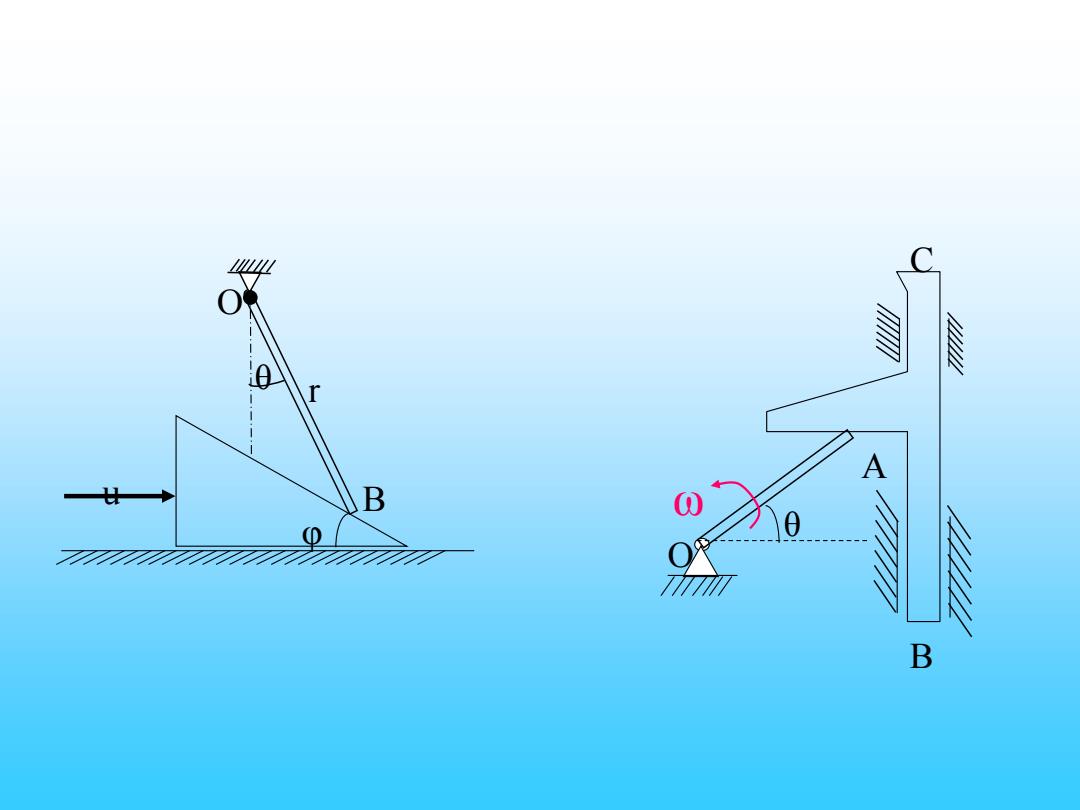
练习题:图示倾角为0=30的尖劈以匀速u=200mm/s沿水平面向右运 动,使杆OB绕定轴转动,r=200√3mm,当已元p时,求0so,8a 解:速度分析如图 Ve Va =Vr= 0 2c0s30° r 0B0 3 牵连为平动,加速度分析如图 acos30°=asin30 5 6=-g3002=- 27
练习题:图示倾角为φ=30o的尖劈以匀速u=200mm/s沿水平面向右运 动,使杆OB绕定轴转动, mm BO BO r = 200 3 ,当 =时,求 , O u B r θ φ va vr ve 2cos30 e a r v v = v = 解:速度分析如图 3 1 = = r va BO aa τ ar aa n 牵连为平动,加速度分析如图 27 3 30 cos30 sin 30 2 = − = − = tg a a n a a

练习题:杆OA长40cm,以匀角速o=0.5rad/s绕O转动,求当0-300 时,曲杆BC的速度和加速度。 解:动点A(OA上),动系BC。 Ve =v cos lwcos 0 =17.3cm/s 牵连为平动, ad=a+a, a=a。+a B de =a si =lo2sim30°=5cm/s2
练习题:杆OA长40cm,以匀角速ω=0.5rad /s 绕O转动,求当θ=300 时,曲杆BC的速度和加速度。 解:动点A(OA上),动系BC。 ω θ C B O A va vr ve ve = va cos = lcos =17.3cm/s 牵连为平动, aa = ae +ar e r n a a = a + a aa ar ae ae = aa sin 2 2 = l sin 30 = 5cm/s
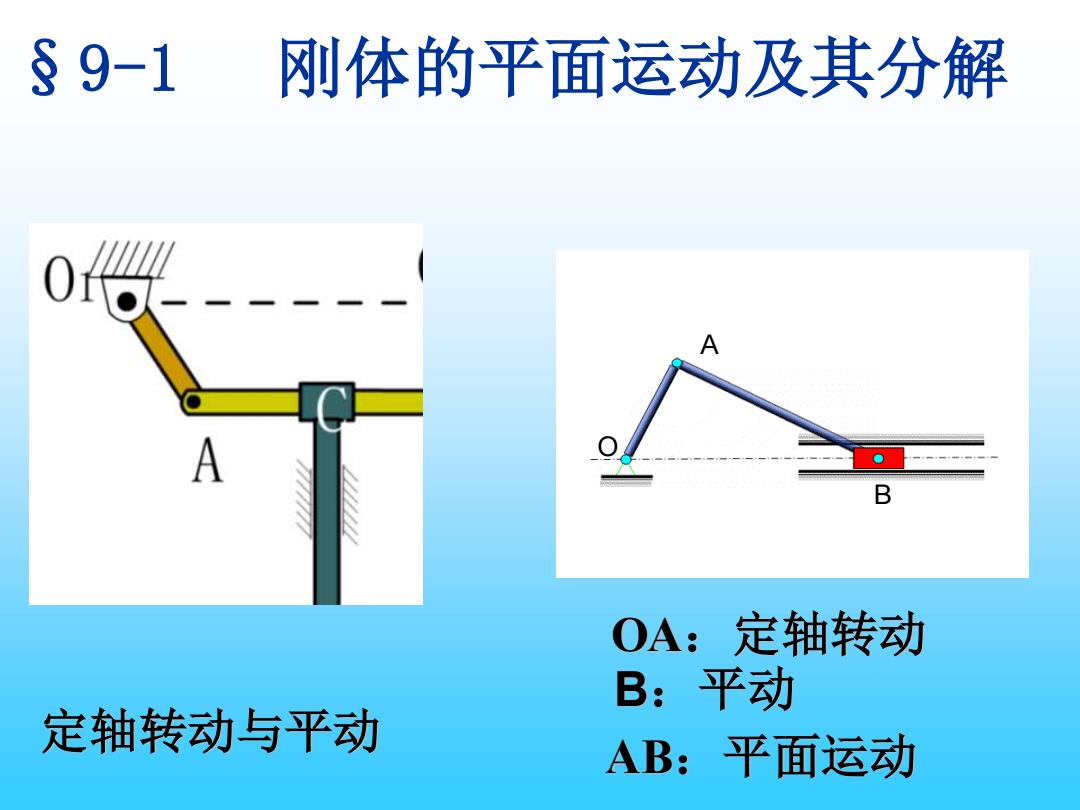
§9-1 刚体的平面运动及其分解 A A OA:定轴转动 B:平动 定轴转动与平动 AB:平面运动
§9-1 刚体的平面运动及其分解 O A B 定轴转动与平动 OA:定轴转动 B:平动 AB:平面运动
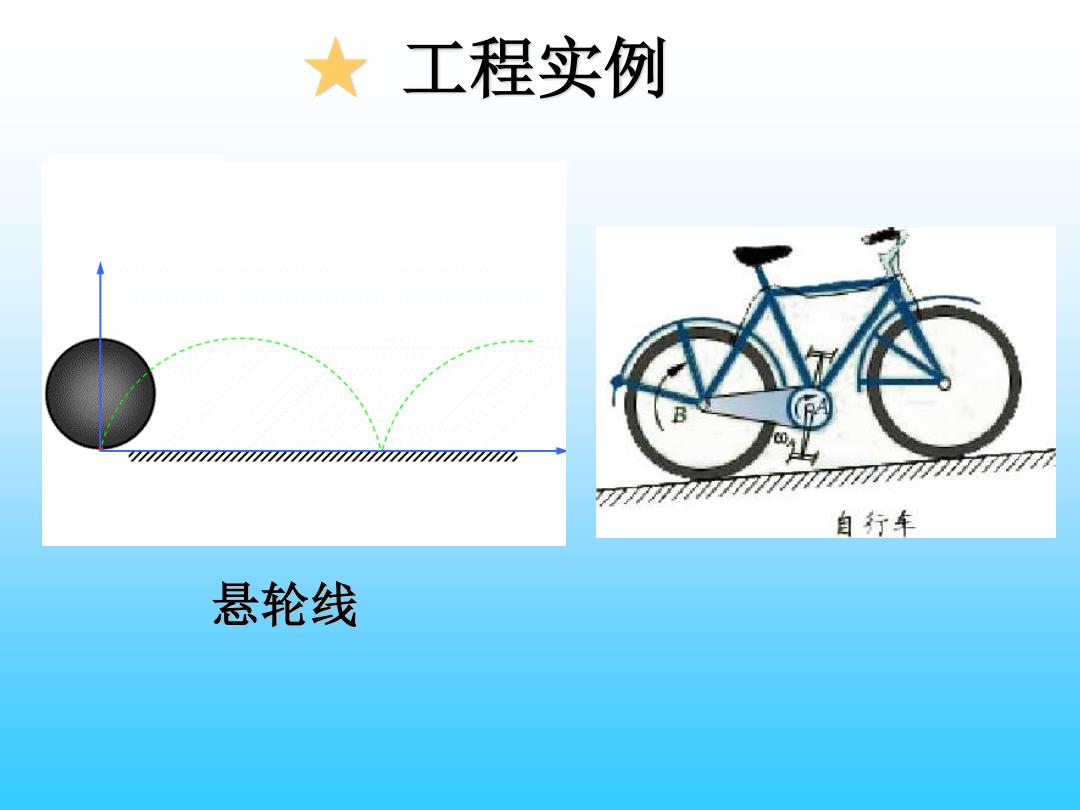
★工程实例 707 自行车 悬轮线
★ 工程实例 悬轮线

静力学之行星齿轮系 行星轮机构
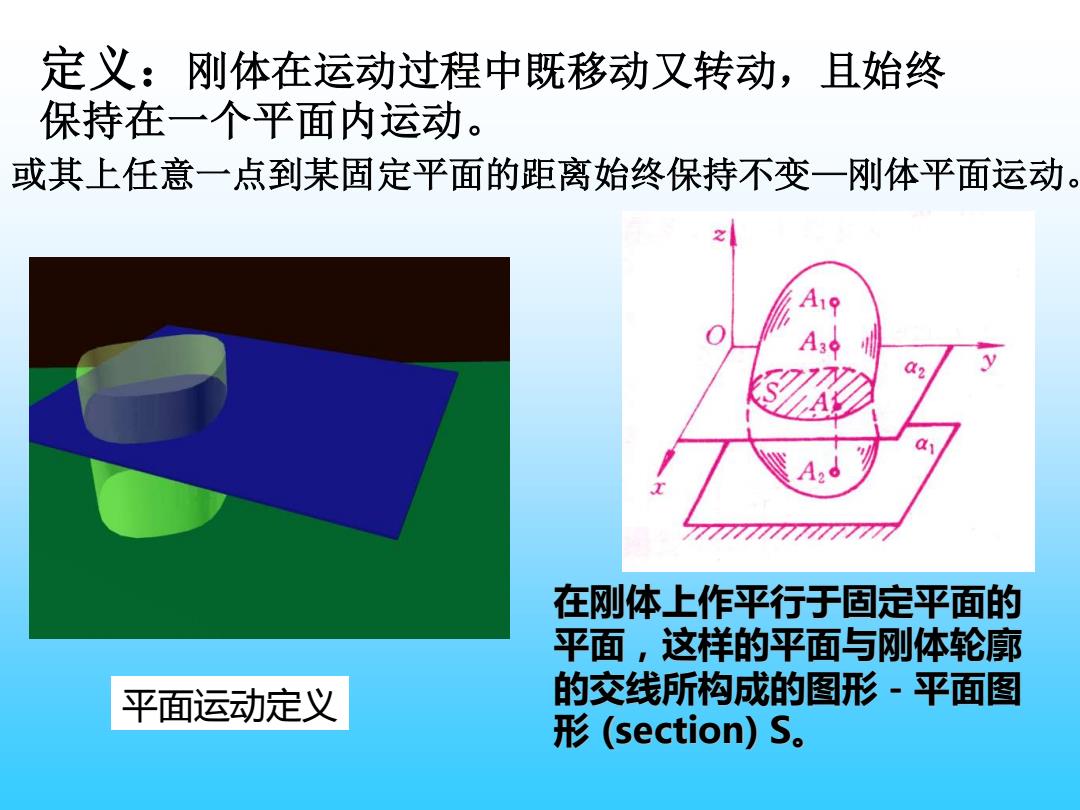
定义:刚体在运动过程中既移动又转动,且始终 保持在一个平面内运动。 或其上任意一点到某固定平面的距离始终保持不变一刚体平面运动 7777777777777 在刚体上作平行于固定平面的 平面,这样的平面与刚体轮廓 平面运动定义 的交线所构成的图形-平面图 形(section)S
定义:刚体在运动过程中既移动又转动,且始终 保持在一个平面内运动。 在刚体上作平行于固定平面的 平面,这样的平面与刚体轮廓 的交线所构成的图形-平面图 形 (section) S。 平面运动定义 或其上任意一点到某固定平面的距离始终保持不变—刚体平面运动
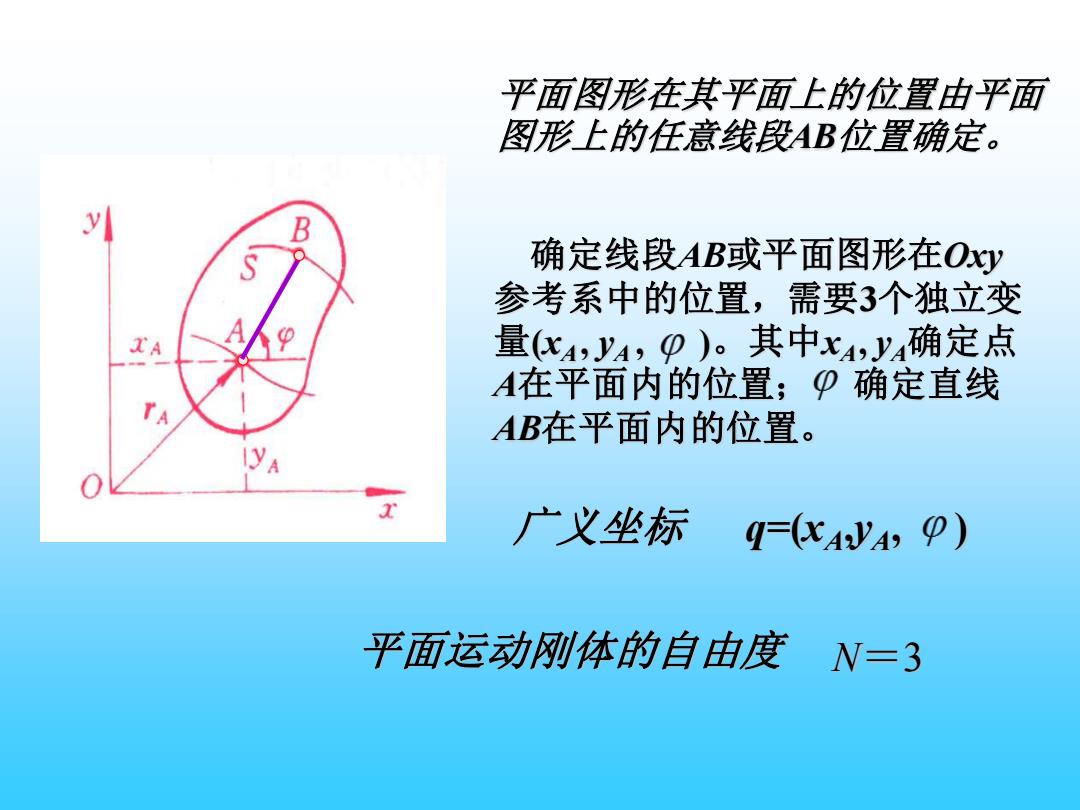
平面图形在其平面上的位置由平面 图形上的任意线段AB位置确定。 y B 确定线段AB或平面图形在Oy 参考系中的位置,需要3个独立变 量(cA,yA,p)。其中x4,Jy4确定点 A在平面内的位置;P确定直线 AB在平面内的位置。 广义坐标 q=(xAVA,P) 平面运动刚体的自由度 N=3
平面图形在其平面上的位置由平面 图形上的任意线段AB位置确定。 平面运动刚体的自由度 N=3 广义坐标 q=(xA,yA, ) 确定线段AB或平面图形在Oxy 参考系中的位置,需要3个独立变 量(xA , yA , )。其中xA , yA确定点 A在平面内的位置; 确定直线 AB在平面内的位置
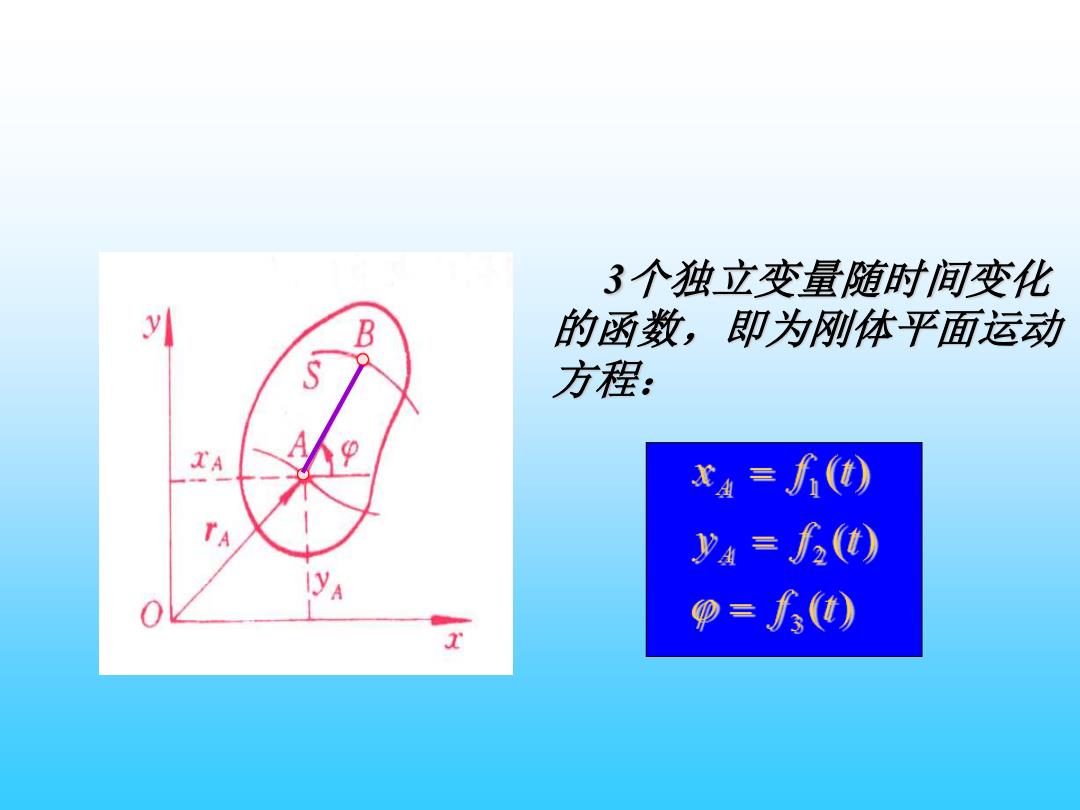
3个独立变量随时间变化 B 的函数,即为刚体平面运动 s 方程: 0 x4=) TA ya三) A =3)
3个独立变量随时间变化 的函数,即为刚体平面运动 方程: