
理论力学复习纲要 静力学: 一、静力学基础 ·约束与约束反力(三力平衡汇交定理、二力杆) ·受力分析 ·力和力矩、力偶和力偶矩 二、力系的平衡(包括空间力系) 平面任意力系的平衡方程在单刚体平衡中的应用 ·刚体系平衡 ·平衡方程在刚体系平衡中的应用(平面) ·考虑有摩擦时物体的平衡(静(动)滑动摩擦、摩擦角)
理论力学复习纲要 静力学: • 约束与约束反力(三力平衡汇交定理、二力杆) • 受力分析 • 力和力矩、力偶和力偶矩 一、静力学基础 二、力系的平衡(包括空间力系) •平面任意力系的平衡方程在单刚体平衡中的应用 • 刚体系平衡 • 平衡方程在刚体系平衡中的应用(平面) • 考虑有摩擦时物体的平衡(静(动)滑动摩擦、摩擦角)

力沿作用线移动: B ∴力是滑动矢量。只适用 于刚体,不适用于变形体 及刚体系统。 反例为:绳子, B B P 777 力线平移 B A MB
力沿作用线移动: A A F F B B 力是滑动矢量。只适用 于刚体,不适用于变形体 及刚体系统。 反例为:绳子, A B C P A B C P ? A F B A F B MB 力线平移
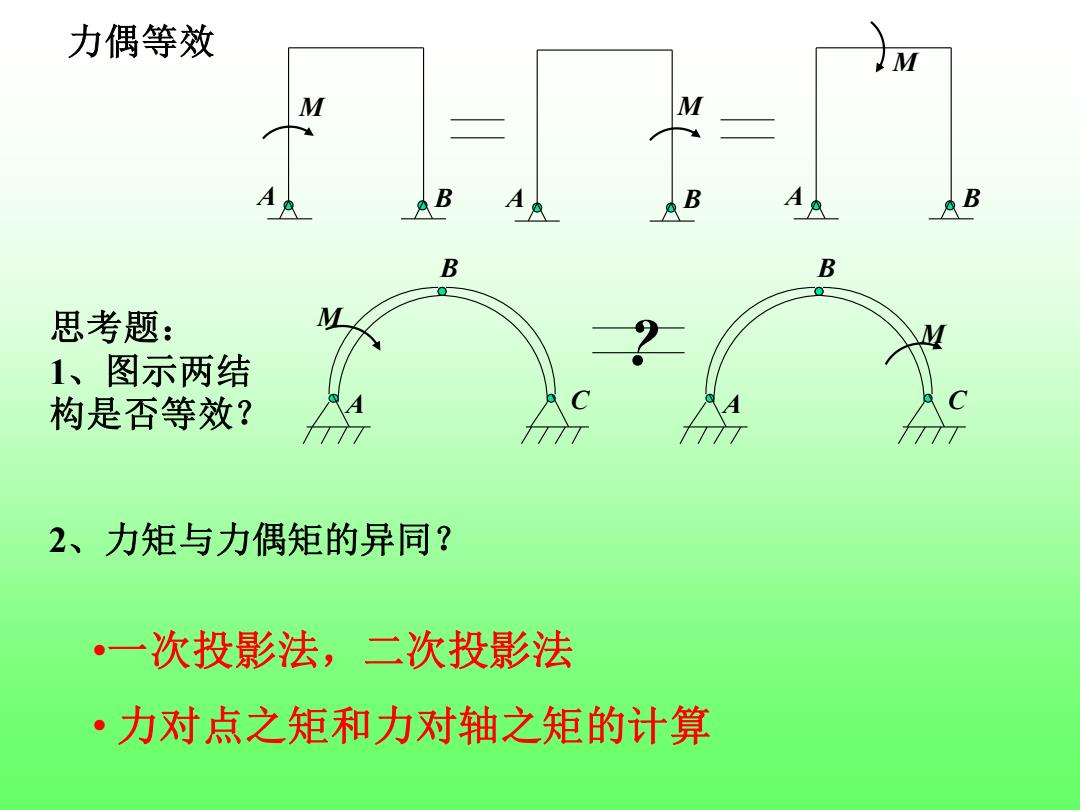
力偶等效 M B B B 思考题: 1、图示两结 构是否等效? 2、力矩与力偶矩的异同? ·一次投影法,二次投影法 ·力对点之矩和力对轴之矩的计算
力偶等效 A B M A B M A B M A B C M A B C ? 思考题: M 1、图示两结 构是否等效? 2、力矩与力偶矩的异同? •一次投影法,二次投影法 • 力对点之矩和力对轴之矩的计算

平面各力系的合成与平衡 平衡方程 力系类型 简化结果 平衡方 FR=0 M。=0 程个数 FR=∑Fi+∑Fj ∑F=0】 F,=0 任意力系 3 M。=∑m,) ∑m=0 几何法:力多边形的封闭边 几何法:力多边形自行封闭 汇交力系 解析法:Fe=∑Fi+∑F,j 解析法∑F=0∑F,=0 2 FR=∑Fi 平行力系 ∑F=0 ∑m=0 2 M,=∑m,() 力偶系 M,=∑m,) ∑m=0 1
平面各力系的合成与平衡 力系类型 简化结果 平衡方程 0 0 ' = = FR Mo 平衡方 程个数 任意力系 ( ) = = + o o i R x y M m F F F i F j ' = = = 0 0 0 m Fx Fy 3 汇交力系 几何法:力多边形的封闭边 解析法: F = F i +F j R x y 几何法:力多边形自行封闭 解析法: = 0 = 0 Fx Fy 2 平行力系 ( ) = = o o i R x M m F F F i ' F = 0 m = 0 x 2 力偶系 = ( ) Mo mo Fi m = 0 1
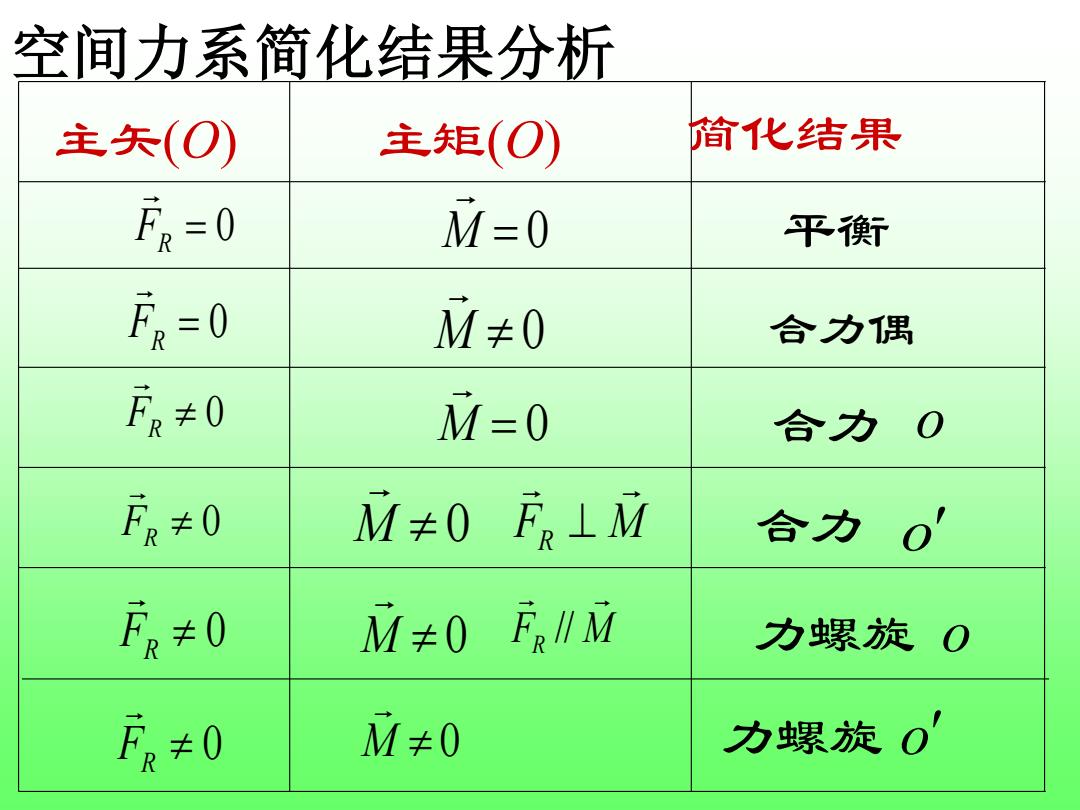
空间力系简化结果分析 主矢(O) 主矩(O) 简化结果 F8=0 M=0 平 F=0 M≠0 合力偶 Fa≠0 M=0 合力0 F≠0 M≠0F⊥M 合力0' 万≠0 M≠0F∥M 力螺旋0 F≠0 M≠0 力螺旋0
空间力系简化结果分析 0 FR M = 0 平衡 合力偶 合力 o 合力 o 0 FR M 0 FR M ⊥ = 0 FR M 0 = 0 FR M = 0 0 FR M 0 0 FR M 0 FR M // 力螺旋 o 力螺旋 o 主矢(O) 主矩(O) 简化结果

图示平面结构,自重不计, C处为光滑铰链。已知: P=100KN,P2=50KN, 0=60°,q=50KN/m,L=4m。 试求固定端A的反力。 L 图示平面结构,自重不计。 已知:M和L,B、C为铰接。 试求固定端A的反力 M
450 P1 P2 q A B D C L L L L 图示平面结构,自重不计, C处为光滑铰链。已知: P1=100KN,P2=50KN, =600 ,q=50KN/m,L=4m。 试求固定端A的反力。 D C B A L M 图示平面结构,自重不计。 已知:M和L,B、C为铰接。 试求固定端A的反力

运动学: 一、运动学基础 ·点的运动 运动方程(直角坐标法、自然法)、速 度与加速度 ·刚体的基本运动 刚体的平动、刚体的定轴转动 二、运动的合成 ·点的合成运动 点的速度合成定理、动系为平动的加速度合成 定理及其应用
运动学: 一、运动学基础 • 点的运动 运动方程(直角坐标法、自然法)、速 度与加速度 • 刚体的基本运动 刚体的平动、刚体的定轴转动 二、运动的合成 • 点的合成运动 点的速度合成定理、动系为平动的加速度合成 定理及其应用

运动学 一刚体的运动 1平动: 各点的轨迹、速度、加速度完全相同,所以刚体的运动可以 用刚体上某一点的运动来代表,这样就可以用点的运动学来求 刚体的运动。 2定轴转动: 刚体上各点的速度加速度 V4=0·r VLAO ap=02.r ap=8.r a8⊥AO B ar=V(an)+(ag)=r.Vo'+E t80=
运 动 学 一 刚体的运动 1 平动: 各点的轨迹、速度、加速度完全相同,所以刚体的运动可以 用刚体上某一点的运动来代表,这样就可以用点的运动学来求 刚体的运动。 2 定轴转动: 刚体上各点的速度加速度 O VA A aB B aB n aB ( ) ( ) 2 4 2 2 2 2 = = = + = + = ⊥ = = ⊥ n B B B n B B B B n B A A a a t g a a a r a r a AO a r v r v AO

3平面运动: VA ·求速度共讲三种方法: ①基点法:是点的合成运动方法, A AB 也是最基本的方法。其概念清楚,是 后两种方法的基础。 VA B 下B=下4+下BA 下B414B VBA AB BA VA A ②投影法:求速度较方便,但求平 面图形的角速度不方便。 VB VE COS B=V coSO
3 平面运动: • 求速度共讲三种方法: 基点法:是点的合成运动方法, 也是最基本的方法。其概念清楚,是 后两种方法的基础。 AB O A B vA vA vB vBA BA v v v v v AB B A A B B A B A B A = = + ⊥ O A B vA vB 投影法:求速度较方便,但求平 面图形的角速度不方便。 vB cos = vA cos
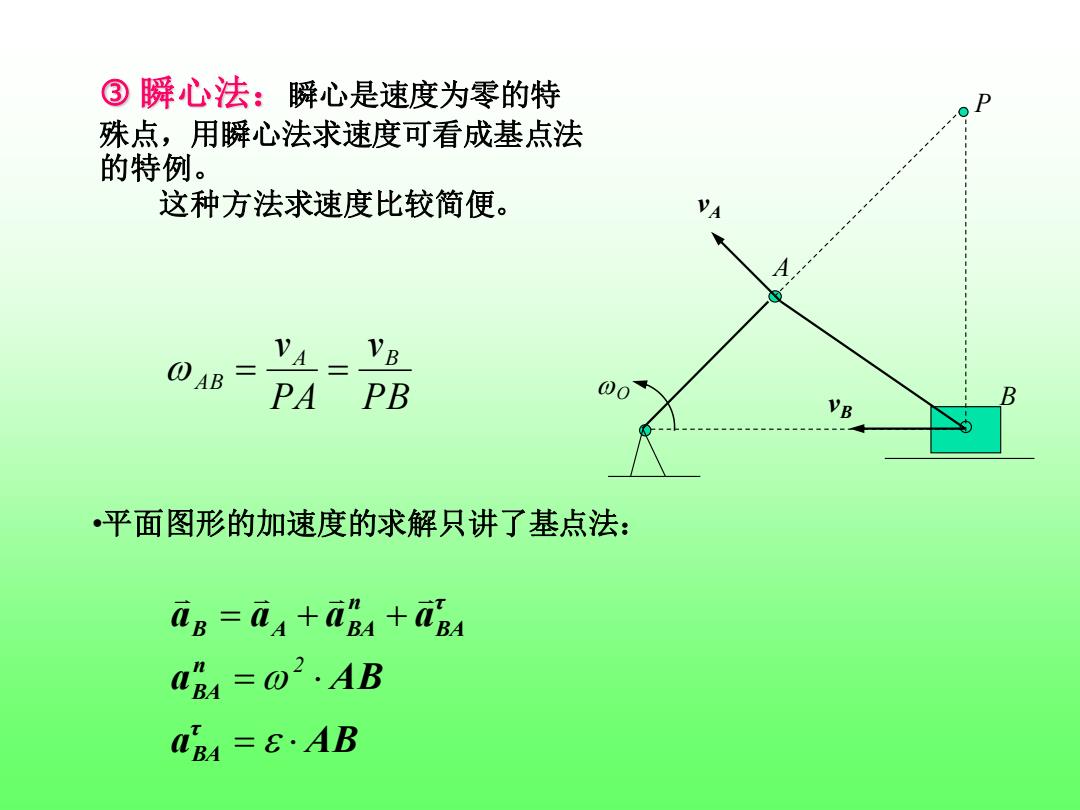
③瞬心法:瞬心是速度为零的特 殊点,用瞬心法求速度可看成基点法 的特例。 这种方法求速度比较简便。 N VB 04B= N PA PB 00 B 平面图形的加速度的求解只讲了基点法: aB aa+am aB aB =@2.AB aBM=8·AB
O A B vA vB 瞬心法:瞬心是速度为零的特 P 殊点,用瞬心法求速度可看成基点法 的特例。 这种方法求速度比较简便。 PB v PA vA B AB = = •平面图形的加速度的求解只讲了基点法: a AB a AB a a a a τ BA n BA τ BA n B A BA = = = + + 2