工程流体力学 Engineering Fluld Mechanics 第五章相似原理和量钢分桥 一、流动的力学相似 日 二、动力相似准则 目录 三、流动相似条件 到 舟 四、近似的模型试验 五、量纲分析法
Engineering Fluid Mechanics 第五章 相似原理和量纲分析 一、流动的力学相似 三、流动相似条件 四、近似的模型试验 二、动力相似准则 五、量纲分析法 目录

工程流体力学 Engineering Fluld Mechanics 第五章 相似原理和量钢分析 实验方法 相似理论 模型试验 数据分析 测量 ◆反映实际流动规律,发现新现象,检验理论结果等 但结果的普适性较差 相似原理和量纲分析 实验流体力学的基本分析手段 3
Engineering Fluid Mechanics 第五章 相似原理和量纲分析 3 实验方法 相似理论 模型试验 数据分析 测量 ◆ 反映实际流动规律,发现新现象,检验理论结果等 但结果的普适性较差 相似原理和量纲分析 实验流体力学的基本分析手段
工程流体力学 Engineering Fluld Mechanics 5-1 流动的力学相似 流动的力学相似是几何相似概念在流体力学中的推广和发展, 它指的是两个流场的力学相似,即在流动空间的各对应点上和各对 应时刻,表征流动过程的所有物理量各自互成一定比例 几何相似 模型与原型的全部对应线性长度的比例相等 长度比例尺 =k 1 b' 翼型的翼弦长b 线性长度 圆柱的直径d 要模型与原型的全部对 应线性长度的比例相等, 特征长度 管道的长度! 则它们的夹角必相等 管壁的绝对粗糙度ε 4
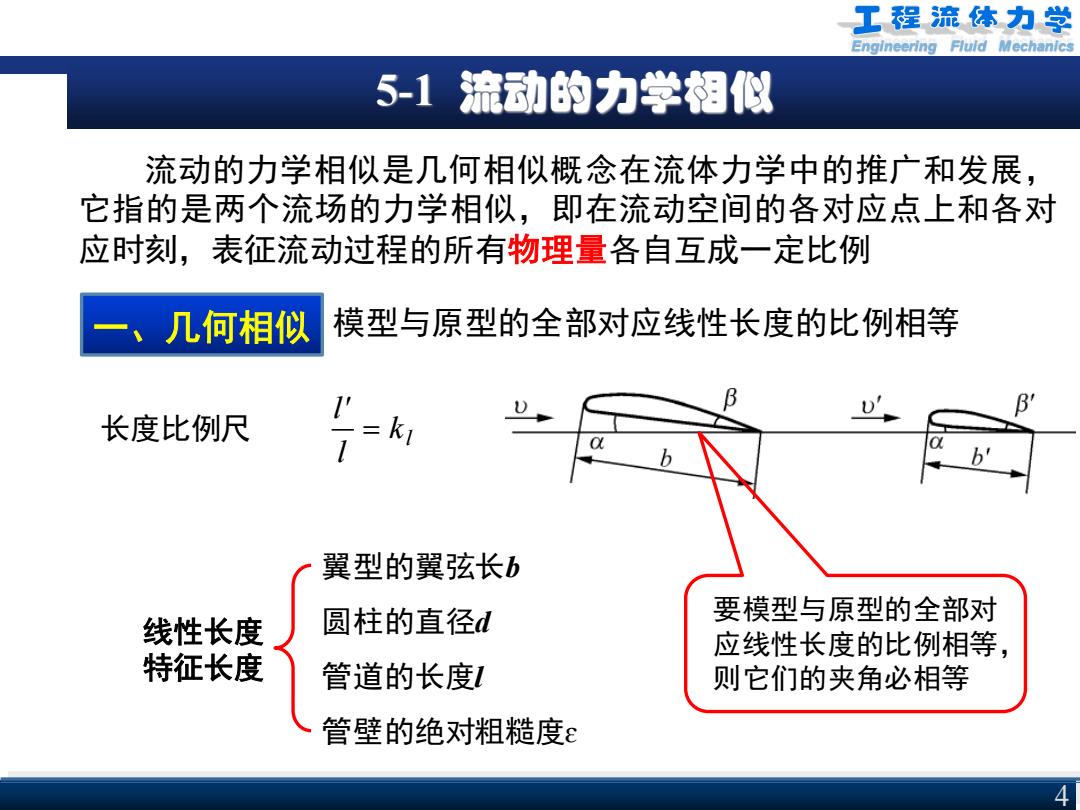
Engineering Fluid Mechanics 5-1 流动的力学相似 4 流动的力学相似是几何相似概念在流体力学中的推广和发展, 它指的是两个流场的力学相似,即在流动空间的各对应点上和各对 应时刻,表征流动过程的所有物理量各自互成一定比例 一、几何相似 模型与原型的全部对应线性长度的比例相等 l k l l' 长度比例尺 = 要模型与原型的全部对 应线性长度的比例相等, 则它们的夹角必相等 线性长度 特征长度 翼型的翼弦长b 圆柱的直径d 管道的长度l 管壁的绝对粗糙度ɛ

工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 一、几何相似 由于几何相似,模型与原型的对应面积、对应体积也必分别 互成一定比例,即 面积比例尺k= = 体积比例尺,= 5
Engineering Fluid Mechanics 5-1 流动的力学相似 5 一、几何相似 由于几何相似,模型与原型的对应面积、对应体积也必分别 互成一定比例,即 面积比例尺 2 2 A l 2 A' l' k k A l = = = 体积比例尺 3 3 V l 3 V' l' k k V l = = =
工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 二、运动相似 模型与原型的流场所有对应点上、对应时刻的流速方向相同 而流速大小的比例相等,即它们的速度场相似。 v" 速度比例尺 k 6
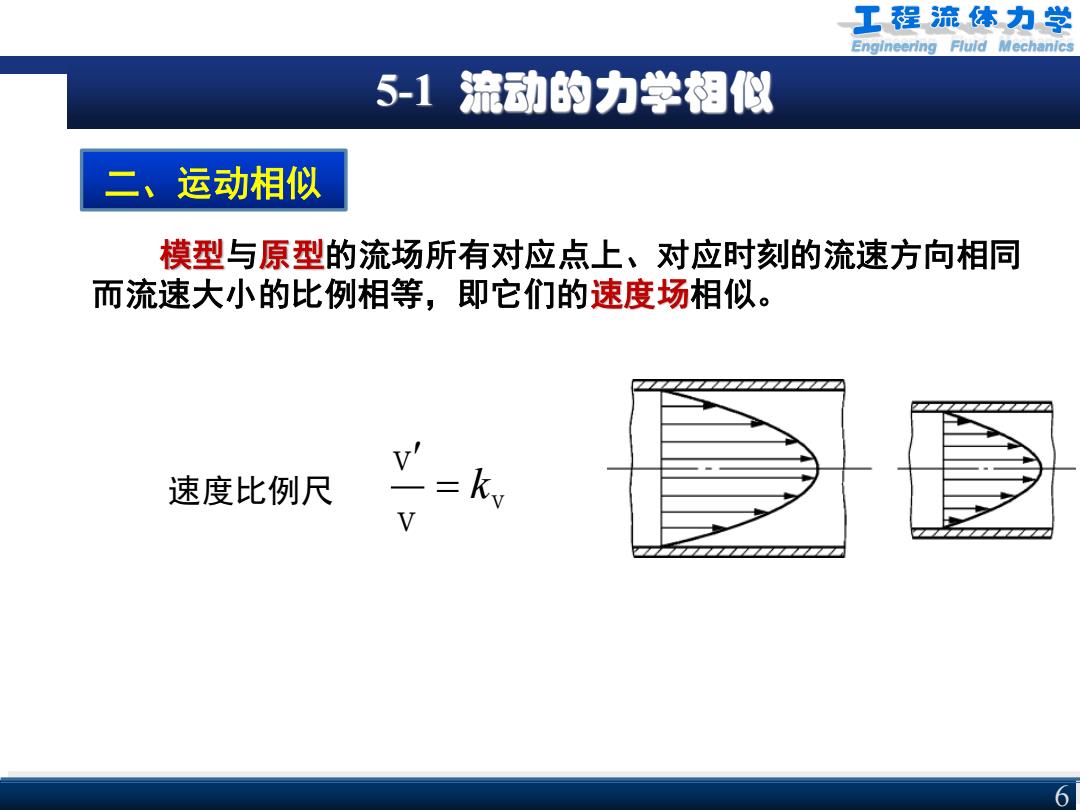
Engineering Fluid Mechanics 5-1 流动的力学相似 6 二、运动相似 模型与原型的流场所有对应点上、对应时刻的流速方向相同 而流速大小的比例相等,即它们的速度场相似。 速度比例尺 v v v k ' =

工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 二、运动相似 1'/w'k, 时间比例尺 k,= Iy k. v'/t' k k 加速度比例尺 a v/t k k k3 -ky 体积流量比例尺 h= =kik, gv Ph k 运动黏度比例尺 =k ky Plt k ' v'/'k 角速度比例尺 k。= o v/l k
Engineering Fluid Mechanics 5-1 流动的力学相似 7 时间比例尺 l t t' l'/ ' k k t l/ k = = = v v v 加速度比例尺 2 a t l a' ' / t' k k / t k k a k = = = = v v v v 体积流量比例尺 2 3 3 3 V q l V t l k q' l' /t' k q k l /t = = = = k k V v 运动黏度比例尺 2 2 2 / / l v l t v l t ' ' ' k k k k v l t k = = = = v / / ω l ω' ' 'l k k ω l k = = = v v v 角速度比例尺 v v v k ' = 二、运动相似
工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 三、动力相似 模型与原型的流场所有对应点作用在流体微团上的各种力 彼此方向相同,而它们大小的比例相等,即它们的动力场相似。 F=-ma F-m'a' 7 应 F W 前 f W-E=ke F。 F W F 8
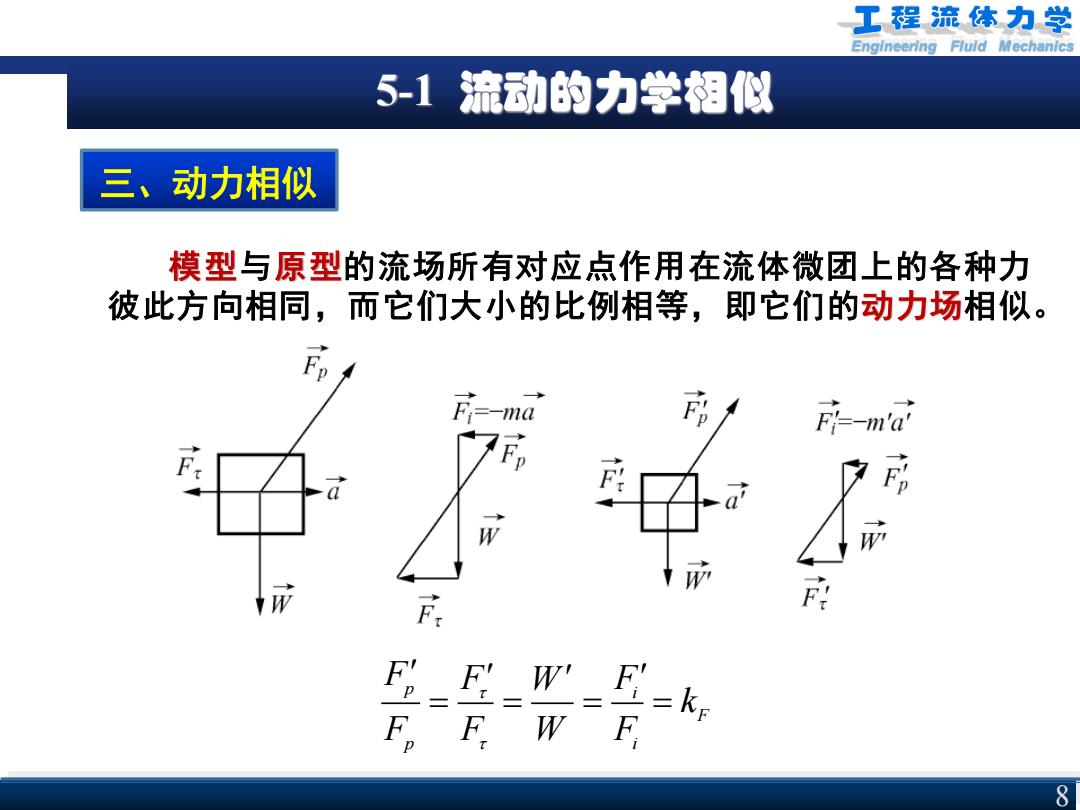
Engineering Fluid Mechanics 5-1 流动的力学相似 8 三、动力相似 模型与原型的流场所有对应点作用在流体微团上的各种力 彼此方向相同,而它们大小的比例相等,即它们的动力场相似。 p i F p i F F F W k F F W F = = = =

工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 三、动力相似 密度比例尺 k,=P'_E Na) Fl(av )kk 力的比例尺 k=kki k? 力矩(功、能)比例尺k,= MFkk=kkiki M Fl 压强(应力)比例尺 p FIA k 功率比例尺 ◇, kp= P kekk Fv 动力黏度比例尺 k= =pY=k,k=k,kk u pv 9
Engineering Fluid Mechanics 5-1 流动的力学相似 密度比例尺 2 2 /( ) /( ) i F F ρ i a l ' ρ' F a'V' k k k ρ F aV k k k k = = = = V v 力的比例尺 2 2 ρ F l k k k k = v 力矩(功、能)比例尺 3 2 M F l l M' F'l' k k k k k k M Fl = = = = v 压强(应力)比例尺 2 / p F p p A p' F' /A' k k k k p F A k = = = = v 功率比例尺 2 3 P F l P' F' ' k k k k k k P F = = = = v v v v 动力黏度比例尺 μ v l μ' ρ'v' k k k k k k μ ρv = = = = v 9 三、动力相似
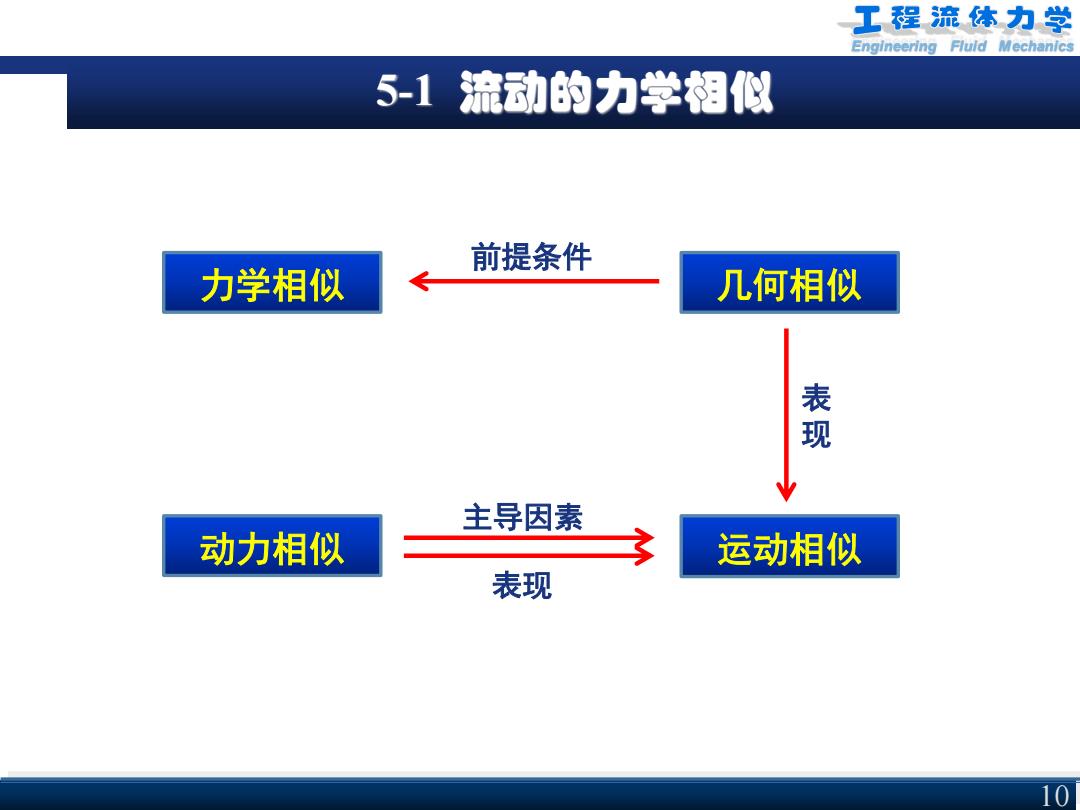
工程流体力学 Engineering Fluld Mechanics 5-1流动的力学相似 前提条件 力学相似 几何相似 泰 主导因素 动力相似 运动相似 表现 10
Engineering Fluid Mechanics 5-1 流动的力学相似 10 力学相似 动力相似 几何相似 前提条件 主导因素 运动相似 表 现 表现
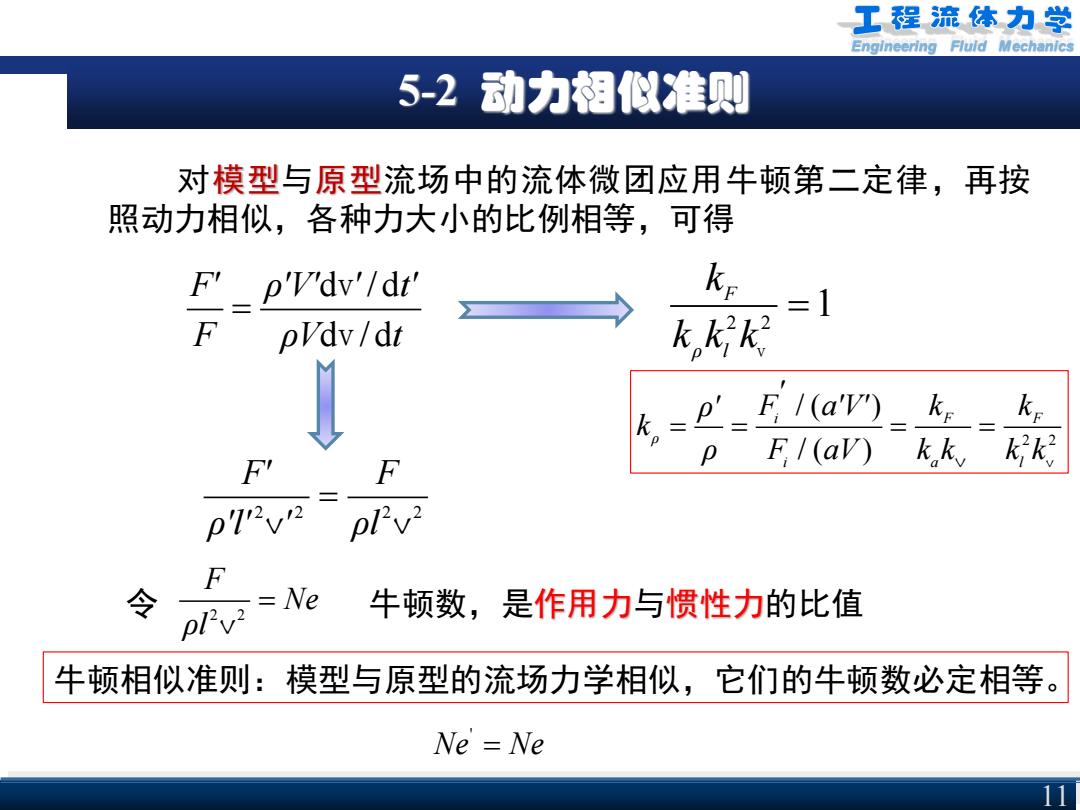
工程流体力学 Engineering Fluld Mechanics 5-2 动力相似准则 对模型与原型流场中的流体微团应用牛顿第二定律,再按 照动力相似,各种力大小的比例相等,可得 F_p'v'dv'/dr' kr 二1 F pVdv/dt k k2k2 k,='=E /(a'v) ke ke F1(av) kk kk? F p72v2 Ne 牛顿数,是作用力与惯性力的比值 牛顿相似准则:模型与原型的流场力学相似,它们的牛顿数必定相等。 Ne Ne
Engineering Fluid Mechanics 5-2 动力相似准则 11 对模型与原型流场中的流体微团应用牛顿第二定律,再按 照动力相似,各种力大小的比例相等,可得 d / d d / d F' ρ'V' ' t' F ρV t = v v 2 2 1 F ρ l k k k k = v 2 2 / ( ) / ( ) i F F ρ i a l ' ρ' F a'V' k k k ρ F aV k k k k = = = = V v 2 2 2 2 F' F ρ'l' ' ρl = v v 令 2 2 F Ne ρl = v 牛顿数,是作用力与惯性力的比值 牛顿相似准则:模型与原型的流场力学相似,它们的牛顿数必定相等。 ' Ne Ne =