工程流体力学 Engineering Fluld Mechanics 第二章流体及其物理性质 一、流体的定义和特征 二、流体作为连续介质的假设 三、流体的密度 目录 四、流体的压缩性和膨胀性 岛 海 五、流体的黏性 六、作用在流体上的力 质量力 表面力 七、液体的表面性质
Engineering Fluid Mechanics 2 第二章 流体及其物理性质 一、流体的定义和特征 三、流体的密度 四、流体的压缩性和膨胀性 二、流体作为连续介质的假设 六、作用在流体上的力 质量力 表面力 五、流体的黏性 七、液体的表面性质 目录
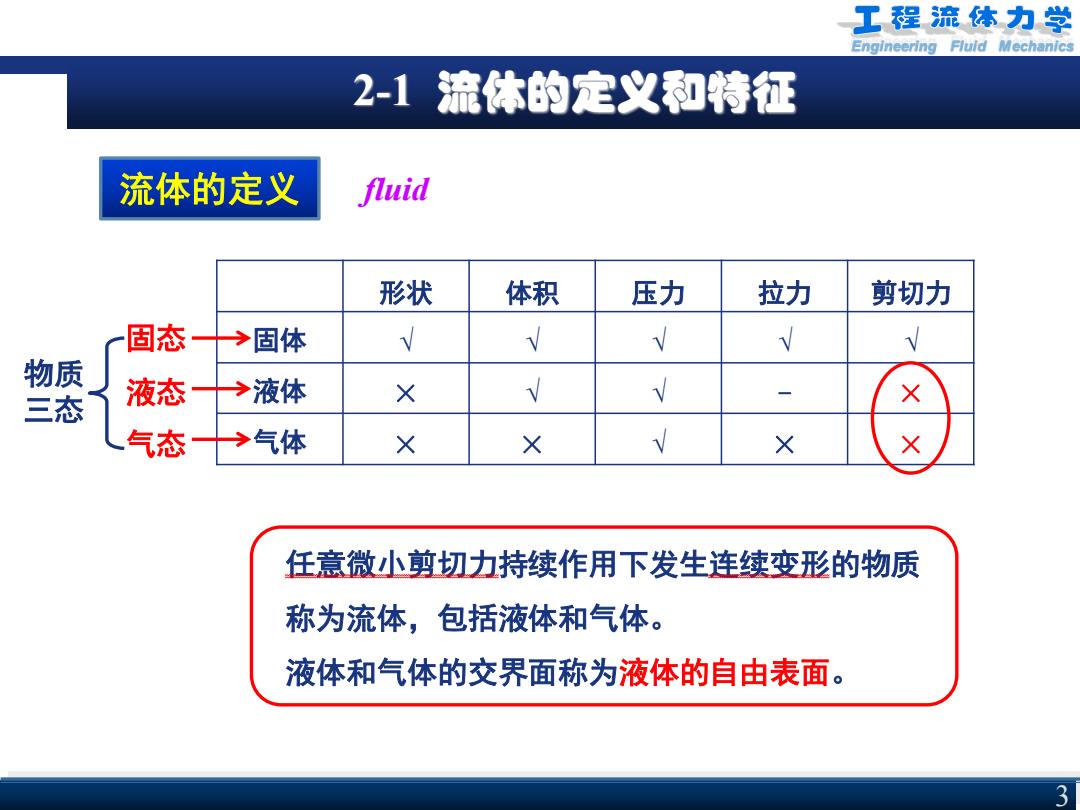
工程流体力学 Engineering Fluld Mechanics 2-1流体的定义和特征 流体的定义 fluid 形状 体积 压力 拉力 剪切力 固态 →固体 物质 三 液态 →液体 × × 气态→气体 × × × × 任意微小剪切力持续作用下发生连续变形的物质 称为流体,包括液体和气体。 液体和气体的交界面称为液体的自由表面。 3
Engineering Fluid Mechanics 3 2-1 流体的定义和特征 流体的定义 fluid 形状 体积 压力 拉力 剪切力 固体 √ √ √ √ √ 液体 × √ √ - × 气体 × × √ × × 任意微小剪切力持续作用下发生连续变形的物质 称为流体,包括液体和气体。 液体和气体的交界面称为液体的自由表面。 固态 液态 气态 物质 三态

工程流体力学 Engineering Fluld Mechanics 2-2 流体作为连续介质的假设 问题的提出 从微观上看,由于构成流体的无数分子之间存在间隙,流体不连续。 从宏观上看,流体力学并不研究流体的微观分子运动,而只研究流体的 宏观机械运动。当所讨论问题的特征尺寸远大于流体的分子平均自由程 时,可将流体视为在时间和空间连续分布的函数。 0°C,1mm3 水含3.4×1019个分子0 气体含2.7×1016个分子 如此大量的分子, 容易取得它们共同 作用的有代表性的 统计平均值 4
Engineering Fluid Mechanics 4 2-2 流体作为连续介质的假设 问题的提出 从微观上看,由于构成流体的无数分子之间存在间隙,流体不连续。 从宏观上看,流体力学并不研究流体的微观分子运动,而只研究流体的 宏观机械运动。当所讨论问题的特征尺寸远大于流体的分子平均自由程 时,可将流体视为在时间和空间连续分布的函数。 0 C,1mm3 水含3.4×1019个分子 气体含2.7×1016个分子 如此大量的分子, 容易取得它们共同 作用的有代表性的 统计平均值
工程流体力学 Engineering Fluld Mechanics 2-2 流体作为连续介质的假设 问题的提出 ) 6r' 黑票票票黑黑黑票票系从黑原原黑黑票系系原思票黑票原思思原思思思票票原原原思思票原票总了 特征体积 5
Engineering Fluid Mechanics 5 2-2 流体作为连续介质的假设 问题的提出 δτ΄ 特征体积
工程流体力学 Engineering Fluld Mechanics 2-2流体作为连续介质的假设 特征体积δr @宏观上充分小 特征体尺度 <流动问题特征长度 在数学上可近似地看成一个几何上没有维度的点 mean free path @微观上充分大 分子平均自由程 <<特征体尺度 包含大量的分子,对分子团进行统计平均后可以得 到稳定数值,少数分子的进出不影响稳定的平均值 6
Engineering Fluid Mechanics 6 2-2 流体作为连续介质的假设 特征体积 δτ΄ 宏观上充分小 微观上充分大 特征体尺度 << 流动问题特征长度 在数学上可近似地看成一个几何上没有维度的点 分子平均自由程 << 特征体尺度 包含大量的分子,对分子团进行统计平均后可以得 到稳定数值,少数分子的进出不影响稳定的平均值 mean free path
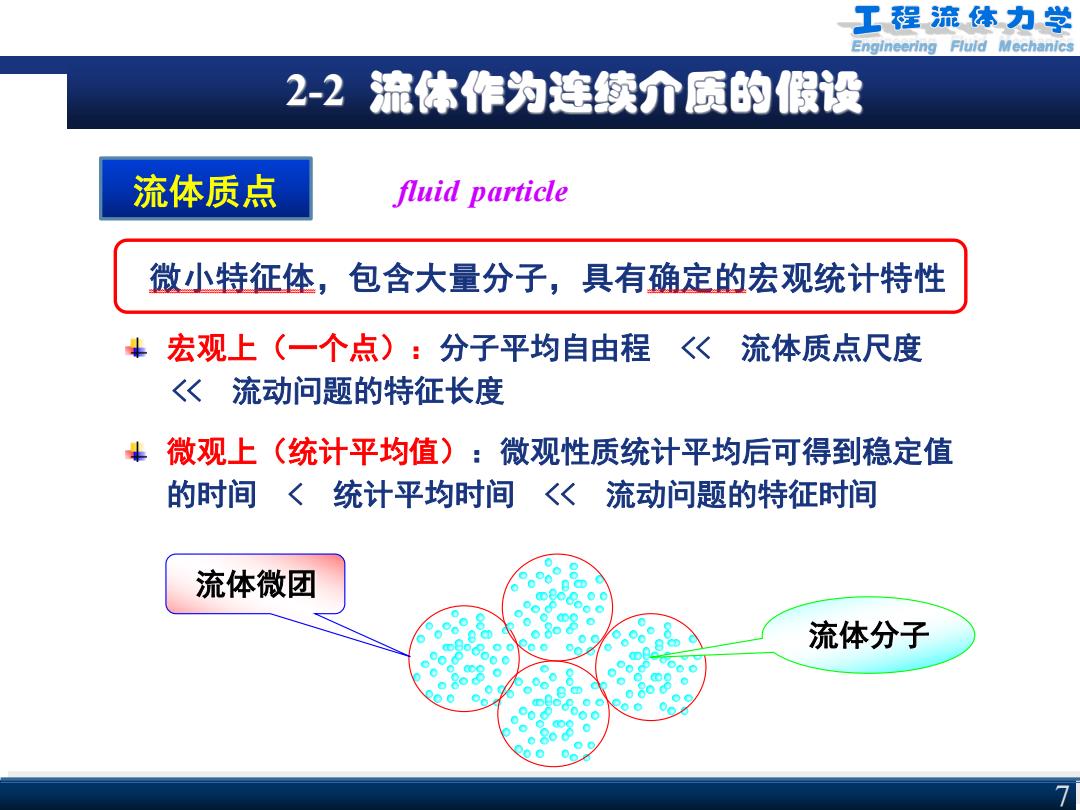
工程流体力学 Engineering Fluld Mechanics 2-2 流体作为连续介质的假设 流体质点 fluid particle 微小特征体,包含大量分子,具有确定的宏观统计特性 宏观上(一个点):分子平均自由程〈 《流体质点尺度 <《流动问题的特征长度 微观上(统计平均值):微观性质统计平均后可得到稳定值 的时间〈 统计平均时间〈<流动问题的特征时间 流体微团 。 流体分子 6o6 o60 0 60
Engineering Fluid Mechanics 7 2-2 流体作为连续介质的假设 流体质点 fluid particle 微小特征体,包含大量分子,具有确定的宏观统计特性 宏观上(一个点):分子平均自由程 << 流体质点尺度 << 流动问题的特征长度 微观上(统计平均值):微观性质统计平均后可得到稳定值 的时间 < 统计平均时间 << 流动问题的特征时间 流体分子 流体微团
工程流体力学 Engineering Fluld Mechanics 2-2 流体作为连续介质的假设 连续介质假设 continuum hypothesis @组成流体的最小物质实体是流体质点 ®流体由无限多的流体质点连绵不断地组成,质点之间无间隙 适用条件 分子平均自由程<流动问题特征体尺寸 不适用 稀薄气体,激波层内等 分子的平均自由 行程和飞行器的 解析函数不适用 特征尺寸相比拟 8
Engineering Fluid Mechanics 8 2-2 流体作为连续介质的假设 连续介质假设 continuum hypothesis 组成流体的最小物质实体是流体质点 流体由无限多的流体质点连绵不断地组成,质点之间无间隙 适用条件 分子平均自由程 << 流动问题特征体尺寸 不适用 稀薄气体,激波层内等 解析函数不适用 分子的平均自由 行程和飞行器的 特征尺寸相比拟

工程流体力学 Engineering Fluld Mechanics 2-2 流体作为连续介质的假设 按照连续介质模型,流体的密度、压强、速度、温度等物理量一般 在时间和空间上都是连续分布,是空间坐标和时间的单值连续可微函数, 这样可以用解析函数的诸多数学工具去研究流体的平衡和运动规律,为 流体力学的研究提供了很大的方便。 问题 密度的定义 体积弹性模量 液体和气体的可压缩性和膨胀性 流体的黏性
Engineering Fluid Mechanics 9 2-2 流体作为连续介质的假设 按照连续介质模型,流体的密度、压强、速度、温度等物理量一般 在时间和空间上都是连续分布,是空间坐标和时间的单值连续可微函数, 这样可以用解析函数的诸多数学工具去研究流体的平衡和运动规律,为 流体力学的研究提供了很大的方便。 问题 密度的定义 体积弹性模量 液体和气体的可压缩性和膨胀性 流体的黏性

工程流体力学 Engineering Fluld Mechanics 2-3流体的密度 密度 表征流体的质量在空间的密集程度,单位为kgm3。 density m 均质流体 0= V 式中,m为流体的质量,为流体的体积。 6m dm 非均质流体 lim 6V→8x' 6V→0 dy 式中,δV为在空间某点取的流体体积,流体的质量为m。 常用流体 的密度值 4℃ 水的密度p=1000kgm3 0℃水银的密度p=13600kgm3 0℃空气的密度p=1.29kg/m3 10
Engineering Fluid Mechanics 10 2-3 流体的密度 密度 density 表征流体的质量在空间的密集程度,单位为 kg/m3 。 均质流体 V m = 式中,m为流体的质量,V为流体的体积。 非均质流体 0 lim V m dm V dV → = = 式中,δV为在空间某点取的流体体积,流体的质量为δm 。 δV → δτ΄ 4℃ 水的密度 ρ = 1000kg/m3 0℃ 水银的密度 ρ = 13600kg/m3 0℃ 空气的密度 ρ = 1.29 kg/m3 常用流体 的密度值

工程流体力学 Engineering Fluld Mechanics 2-3流体的密度 流体的比体积(比容) specific volume 单位质量流体占有的体积,即密度的倒数,单位mg。 U= 热力学常用 m 流体的相对密度 某流体的密度p与4℃时水的密度p的比值 d=prlpw w=1000 kg/m3 混合气体的密度 p=pa+p,a+…+p,an=∑Pa 体积 百分比 重度 表示单位体积物质的重量,单位N/m3。 specific weight Y=pg 水力学常用
Engineering Fluid Mechanics 11 2-3 流体的密度 流体的比体积(比容) specific volume 单位质量流体占有的体积,即密度的倒数,单位m3 /kg。 1 = = m V 热力学常用 重度 specific weight 表示单位体积物质的重量,单位N/m3 。 = g 水力学常用 1 1 2 2 1 n n n i i i = = + + + = 某流体的密度f与4℃时水的密度w的比值 d =f /w w= 1000 kg/m3 流体的相对密度 混合气体的密度 体积 百分比