
工程流体力学 Engineering Fluld Mechanics 第四章 流体运动学和动力学基础 流体运动的描述方法 二、流动的分类 0包 三、迹线 流线 四、流管 流束 流量 水力半径 目录 五、系统 控制体 输运公式 六、连续方程 围 钟 七、动量方程 动量矩方程 八、能量方程 九、伯努利方程及其应用 十、沿流线主法线方向压强和速度的变化 十一、粘性流体总流的伯努利方程
Engineering Fluid Mechanics 2 第四章 流体运动学和动力学基础 一、流体运动的描述方法 三、迹线 流线 四、流管 流束 流量 水力半径 二、流动的分类 六、连续方程 五、系统 控制体 输运公式 十、沿流线主法线方向压强和速度的变化 目录 七、动量方程 动量矩方程 八、能量方程 九、伯努利方程及其应用 十一、粘性流体总流的伯努利方程
工程流体力学 Engineering Fluld Mechanics 4-1 流体运动的描迹方法 流体运动时,表征运动特征的运动要素一般随时间空间 而变,而流体又是众多质点组成的连续介质,流体的运动是 无穷多流体运动的综合。 怎样描述整个流体的运动规律呢? 拉格朗日法 欧拉法 流体质点 空间点 3
Engineering Fluid Mechanics 4-1 流体运动的描述方法 3 流体运动时,表征运动特征的运动要素一般随时间空间 而变,而流体又是众多质点组成的连续介质,流体的运动是 无穷多流体运动的综合。 怎样描述整个流体的运动规律呢? 拉格朗日法 欧拉法 流体质点 空间点
工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描迹方法 拉格朗日法 质点系法/随体法/跟踪法 把流体质点作为研究对象,跟踪每一个质点,描述其运动过程 中流动参数随时间的变化,综合流场中所有流体质点,来获得整个 流场流体运动的规律。 M 设某一流体质点在仁t,时刻占据起 始坐标(a,b,c),t为时间变量 x=x(a,b,c,t) C y 流体质点 运动方程 y=y(a,b,c,t) z=z(a,b,c,t) 4
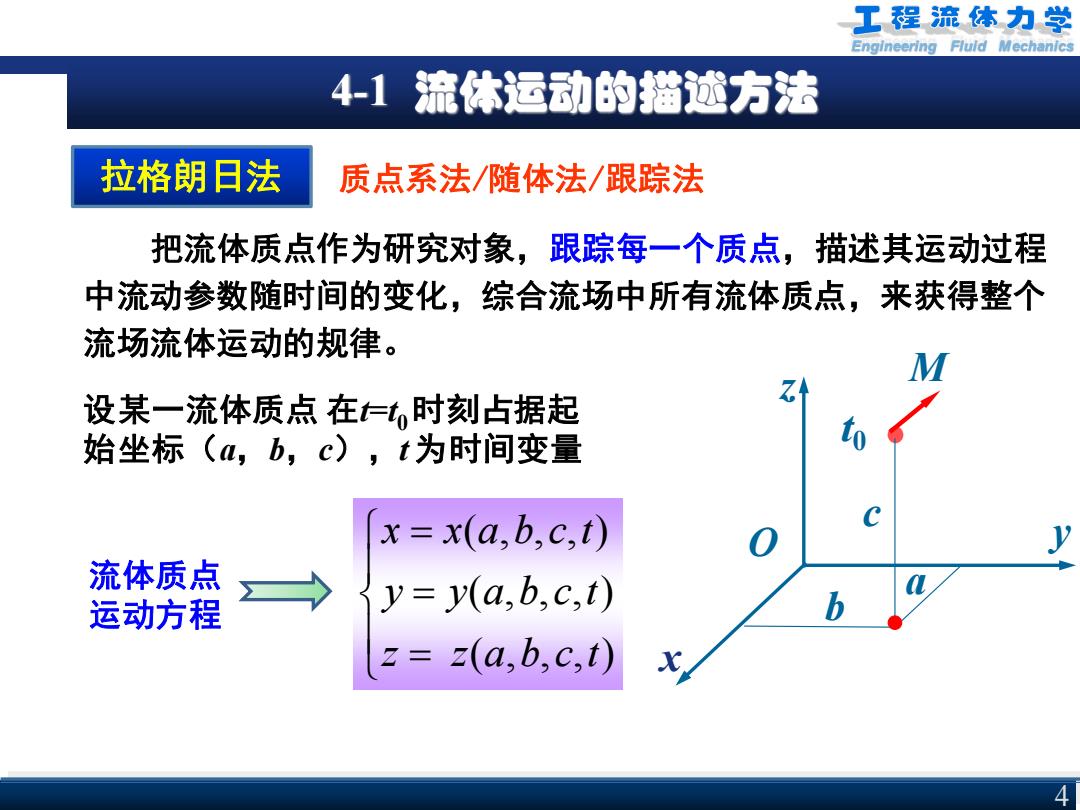
Engineering Fluid Mechanics 4-1 流体运动的描述方法 4 拉格朗日法 把流体质点作为研究对象,跟踪每一个质点,描述其运动过程 中流动参数随时间的变化,综合流场中所有流体质点,来获得整个 流场流体运动的规律。 质点系法/随体法/跟踪法 z O y a b c z t0 M t x 设某一流体质点 在t=t0 时刻占据起 始坐标(a,b,c),t 为时间变量 流体质点 运动方程 ( , , , ) ( , , , ) ( , , , ) x x a b c t y y a b c t z z a b c t = = =

工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描迹方法 拉格朗日法 质点系法 t时刻,流体质点运动到空间坐标 (x,y,z) x=x(a,b,c,t) y=y(a,b,c,t) Z y z=z(a,b,c,t) X 式中,a,b,c,t为拉格朗日变数 (a,b,c)对应流体微团或液体质点 5
Engineering Fluid Mechanics 4-1 流体运动的描述方法 5 拉格朗日法 t 时刻,流体质点运动到空间坐标(x,y,z) 质点系法 z x O y a x b y c z t0 t M 式中,a,b,c,t 为拉格朗日变数 (a,b,c)对应流体微团或液体质点 ( , , , ) ( , , , ) ( , , , ) x x a b c t y y a b c t z z a b c t = = =

工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描迹方法 拉格朗日法 质点系法 给定(a,b,c),t变化时,该质点的轨迹方程确定; 不同(M,b,c),t不变,表示在选定时刻流场中流体质点的位 置分布。 Ox(a,b,c,t) ux x=x(a,b,c,t) 8t 流体质点 Oy(a,b,c,t) 的速度为 y=y(a,b,c,t) 8t z =z(a,b,c,t) Oz(a,b,c,t) u. 8t
Engineering Fluid Mechanics 4-1 流体运动的描述方法 拉格朗日法 给定(a,b,c),t 变化时,该质点的轨迹方程确定; 质点系法 不同(a,b,c),t 不变,表示在选定时刻流场中流体质点的位 置分布。 流体质点 的速度为 ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) x y z x a b c t u t x x a b c t d y a b c t y y a b c t u dt t z z a b c t z a b c t u t = = = = = =

工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描迹方法 拉格朗日法 质点系法 流体质点的加速度为 a,a,(a,b,c,t)= Ou,(a,b,c,t) 8x(a,b,c,t) 8t 0t2 ay a,(a,b,c,t)= du,(a,b,c,t)8y(a,b,c,t) 8t 812 a:=a.(a,b,c,t)= Ou.(a,b,c,1) a2z(a,b,c,t) 8t 812
Engineering Fluid Mechanics 4-1 流体运动的描述方法 拉格朗日法 质点系法 流体质点的加速度为 2 2 2 2 2 2 ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) x x x y y y z z z u a b c t x a b c t a a a b c t t t u a b c t y a b c t a a a b c t t t u a b c t z a b c t a a a b c t t t = = = = = = = = =

工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描述方法 拉格朗日法 质点系法 x=x(a,b,c,t) 问题 y=y(a,b,c,t) (a,b,c)limited fluid points z=z(a,b,c,t) @每个质点运动规律不同,很难跟踪足够多质点 @数学上存在难以克服的困难 @实用上,不需要知道每个质点的运动情况 因此,该方法在工程上很少采用
Engineering Fluid Mechanics 4-1 流体运动的描述方法 拉格朗日法 质点系法 问题 ( , , , ) ( , , , ) ( , , ) limited fluid points ( , , , ) x x a b c t y y a b c t a b c z z a b c t = = = 每个质点运动规律不同,很难跟踪足够多质点 数学上存在难以克服的困难 实用上,不需要知道每个质点的运动情况 因此,该方法在工程上很少采用
工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描述方法 欧拉法 流场法(站岗法) 研究运动要素分布场 研究流体质点在通过某一空间点时流动参数随时间的变化规律。 该法是对流动参数场的研究,例如速度场、压强场、密度场、温度 场等。 采用欧拉法,可将流场中任何一个运动要素表示为空间坐标 (x,y,z)和时间t的单值连续函数。 液体质点在任意 u,=u,(x,y,z,t) p=p(x,y,z,t) 时刻t通过任意 空间固定点化,y, 4y=4(x,y,2,t) p=p(x,y,z,t) z)时的流速为 u.=u(x,y,2,t) T=T(x,y,z,t) 式中,七y,乙,t称为欧拉变数
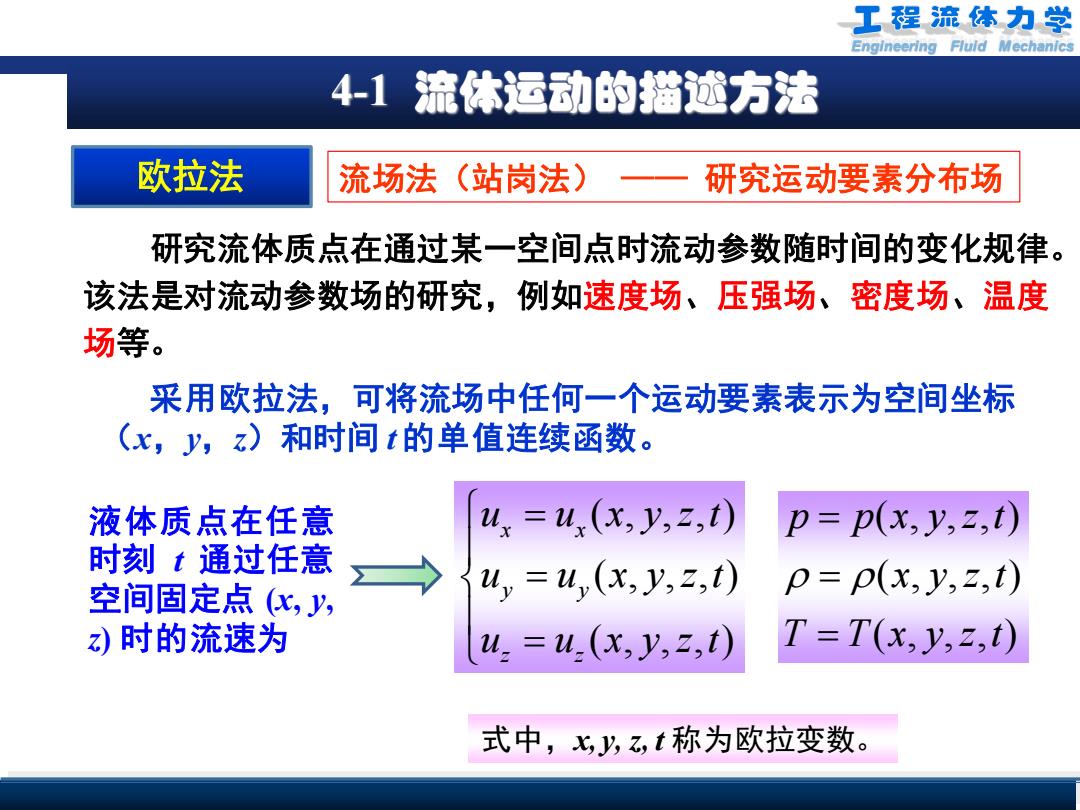
Engineering Fluid Mechanics 4-1 流体运动的描述方法 欧拉法 流场法(站岗法) —— 研究运动要素分布场 研究流体质点在通过某一空间点时流动参数随时间的变化规律。 该法是对流动参数场的研究,例如速度场、压强场、密度场、温度 场等。 采用欧拉法,可将流场中任何一个运动要素表示为空间坐标 (x,y,z)和时间 t 的单值连续函数。 式中,x, y, z, t 称为欧拉变数。 ( , , , ) ( , , , ) ( , , , ) p p x y z t x y z t T T x y z t = = = ( , , , ) ( , , , ) ( , , , ) x x y y z z u u x y z t u u x y z t u u x y z t = = = 液体质点在任意 时刻 t 通过任意 空间固定点 (x, y, z) 时的流速为
工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描述方法 欧拉法 流场法 研究运动要素分布场 令心,y,)为常数,t为变数 表示在某一固定空间点上,流体质点的 运动参数随时间的变化规律。 令(x,y,z)为变数,t为常数 表示在同一时刻,流场中流动参数的分 布规律。即在空间的分布状况
Engineering Fluid Mechanics 4-1 流体运动的描述方法 欧拉法 流场法 —— 研究运动要素分布场 令(x , y , z)为常数,t 为变数 表示在某一固定空间点上,流体质点的 运动参数随时间的变化规律。 令(x , y , z)为变数,t 为常数 表示在同一时刻,流场中流动参数的分 布规律。即在空间的分布状况

工程流体力学 Engineering Fluld Mechanics 4-1流体运动的描迹方法 欧拉法 流场法一 研究运动要素分布场 du,(x,y,z,t) ax dt 液体质点通过任意空 du,(x,y,z,t) 间坐标时的加流速 dt du.(x,y,z,t) a,= dt 式中,(ax,4,a)为通过空间点的加速度分量
Engineering Fluid Mechanics 4-1 流体运动的描述方法 11 液体质点通过任意空 间坐标时的加流速 d ( , , , ) d d ( , , , ) d d ( , , , ) d x x y y z z u x y z t a t u x y z t a t u x y z t a t = = = 欧拉法 流场法 —— 研究运动要素分布场 式中, (ax , ay , az ) 为通过空间点的加速度分量