
高速运动物体的表观长度和 Terrell转动 胡 望雨 (北京大学) 定于S系中的观察而P上.在P面上反映,尺子影象 一、运动尺子的表观长度 在阐述狭义相对论的文草或数科书中,处处要提 到“观察者”,且总是把“观察者”依附于某一参照系,以 说明某事件的空-时特征,这无疑是一种方便的表述方 法。但当我们读到“从8系中的观察者看来…”这一 经常使用的口头语时,就需十分小心了。这种表述容 易造成一种假象,以为某观察者真的可看到或观察到 他所在的参照系中在同一瞬时发生的各事件的总图 象。事实上这是不可能的,因为观察者只能直接了解 他所在地点的事件,而别的地方在同一瞬时发生的事 件只能依靠某种信号(如光信号)的传递才能得知.一 S系 切信号的传递速度都是有限的,这使观察者看到的或 图1 观察到的总图象实际上是在不同时刻发生的各事件的 组合,是一种发生了畸变的图象。前面所引的那种表 的光信号必定要同时到达该面(可设想用高速快门斑 述只不过是指出测量是在8系中进行的,它绝不意味 取物象的情景)。由于光信号传递速度的有限性,同时 着观察者真的直接去看或是确实看到了,如果观察者 到达P面的光信号却是在不同时刻从尺子上发出的. 真的用眼去看,或想象用照相办法去记录某事物,那么 例如形成尺子A端影象的光信号是在某时刻t从A端 他所得到的结果就不是该事物的本来面目,,因为在所 发出的,则形成B端影象的光信号一定是在较晚的时 看到的现象中已包含了其它因素:光信号的传输特 刻t十△,即B端运动到B处才发出。设观察方向用 征。一个简单的例子是运动尺子的长度.当本征长度 日角表示,我们来计算P面上记录到的尺子影象的宽度 为L。的尺子沿其长度方向相对于观察者以速度节运 b。从图1的儿何关系不难得到: 动时,对观案者来说,尺子长度要产生洛仑兹收缩,长 g8=6 度变为 c At b=Lsin0+u△tsin0 -g (1) 从以上两式可得 Lcsin 6 但观察者用眼看到的或照相记录到的尺子长度并不是 c-vcos0= sin0L 1-”cos9 工,而是另一个长度,我们不仿称之为表观长度.我们 式中L是尺子在8系中的长度,把(1)式代入,得 用最浅显的道理来说明这点, 在图1中,8系中的观察者通过眼睛或照相记录 b= V1-5 来观察尺子的长度,观察者的视线自然要正对着尺 -Le sin 0 (2) 子。假定尺子的线度比起它离观察者的距离来要小得 1-名cos0 多,则从尺子上各点发出的光信号均将垂直人射到固 所以尺子的表观长度为 ·21
高速运动物体的表观长度和 Terrell转动 胡 望 雨 (北京 大学 ) 一 、 运 动尺 子 的表观 长 度 定子 系中的观察而P .在P而上反映, 尺子影象 在 阐述狭义相对论的文章或数科书 中, 处处要提 到“观察者”,且总是把 观 察者 ”依附于某一参照系 ,以 说明某事件 的空一时特征 ,这 无疑是一种方便的表述 方 法.但 当我们读 到“从 系中的观察者看来 …… 这一 经 常使用的 口头语时 , 就 需十分小心 了.这种表述容 易造成一种 假象, 以为 某观 察者真的可看 到或观 察到 他所在 的参照系中在 同一 瞬 时发 生的 各事 件的 总 图 象.事 实上这是 不可能的, 因为观察者只能直接 了解 他所在地点的事件, 而别的地方在同一瞬时发生 的事 件只能依靠某种信号(如光信号 )的传递 才能得知. 一 切信号的传递速度都是有 限的, 这 使观察者看 到的或 观 察到的总图象实际 上是 在不 同时 刻发生 的各 事件 的 组 合, 是 一种发生 了畸变的图象.前 面所 弓f的那种表 述 只不过是 指出测量是在 系中进 行的, 它绝不意味 者 观察者真的直 接去看或是 确实看 到了. 如果观察者 真的用眼去 看 ,或想象用照相办法去记录某事物 ,那 么 他 所得 到的结果就不是该事物 的本来面 目,、因为在 所 看 到的现象中已包含 了 其它 因素。 光信号 的传 输 特 征.一个 简单的例子是运 动尺 子的长度. 当本征长度 为 厶 的尺子沿其长度方向相对 于 观察 者以 速 度 ,运 动 时,对观察者来说 ,尺子 长度要产生洛 仑兹收缩, 长 度 变为 L = L。 翻 1 .S系 的光信号必定要 同时到 达该面 (可设想用高速快门摄 取物象的情景). 由于光信号传递速度的有限性 ,同时 到达P面 的光 信号 却是在不 同时刻从尺子上 发出的. 例如形成尺子 端影象的光 信号是 在某 时刻 从 端 发出的, 则形成 B端影 象的光信号一定是在较晚的时 刻 +At,即 B端运动到 B 处才发出. 设观察方 向用 0角表示 ,我们来 计算 P面上 记录到的尺子影象的宽度 6.从 图 1的几何关系不难得到。 tg 目= b= LsinO+ vA tsin0 (1) 从以上两式可得 但 观察者用眼看到的或照相记录到的尺子长度并 不是 ,而是 另一个长度 ,我们不仿称之为表观 长度. 我们 用最浅显的道理来说 明这点. 在 图 1中, 系 中的观察者通过眼睛或照相记录 来观察尺子的长度, 观察者的视 .线 自然要 正对 着尺 子. 假定尺子的线度比起它离观察者的距离来要小得 多, 则从尺子 上各 点发 出的光 信号 均将垂直入射到 固 6 : : —1 v — cosO 墨1一÷COS0
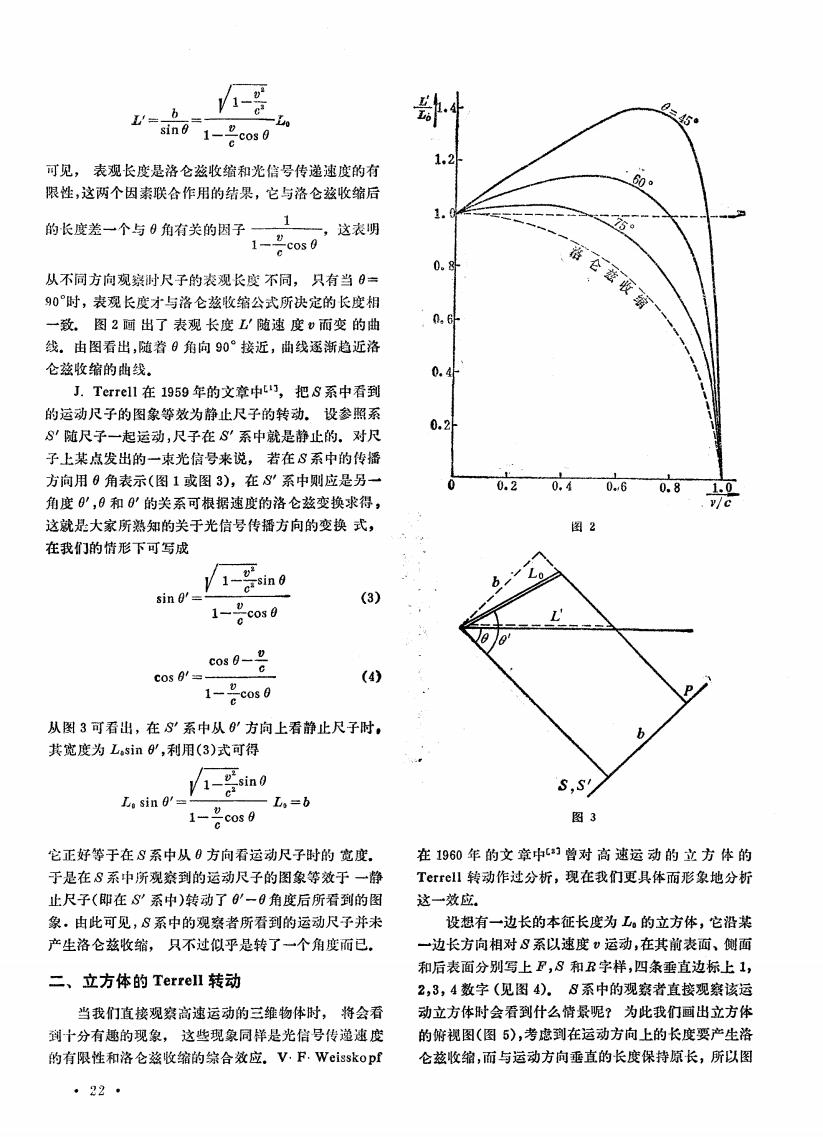
1、2 V=b 0=45° sin61-”c os0 可见,表观长度是洛仑兹收缩和光信号传递速度的有 限性,这两个因素联合作用的结果,它与洛仑兹收缩后 60 的长度差一个与0角有关的因子1 1、 一,这表明 75 ccos 从不同方向观浆时尺子的表观长度不同,只有当9= 90时,表观长度才与洛仑兹收缩公式所决定的长度相 落仑兹暇缩 一致.图2画出了表观长度L随速度而变的曲 线。由图看出,随着9角向90°接近,曲线逐渐趋近洛 仑兹收缩的曲线。 0.4 J.Terrel1在1959年的文章中t,把8系中看到 的运动尺子的图象等效为静止尺子的转动。设参照系 0.2 S”随尺子一起运动,尺子在S'系中就是静止的。对尺 子上某点发出的一束光信号来说,若在8系中的传播 方向用0角表示(图1或图3),在S”系中则应是另一 0.2 0。 06 0.8 1.0 角度日',9和0'的关系可根据速度的洛仑兹变换求得, V/c 这就是大家所熟知的关于光信号传播方向的变换式, 图2 在我们的情形下可写成 1 osin 0 sin 0'= 1 (3) c cos0 c03B" cos ! c (4) 1、0 cos0 从图3可看出,在S系中从'方向上看静止尺子时, b 其宽度为Lsin0,利用(3)式可得 sin 1- S,S! Lo sin 0=- 1也 -L,=b ccos g 图3 它正好等于在8系中从0方向看运动尺子时的宽度. 在1960年的文章中)曾对高速运动的立方体的 于是在8系中所观笨到的运动尺子的图象等效于一静 Terrell转动作过分析,现在我们更具体而形象地分析 止尺子(即在S”系中)转动了'一0角度后所看到的图 这一效应. 象。由此可见,8系中的观察者所看到的运动尺子并米 设想有一边长的本征长度为工。的立方体,它沿某 产生洛仑兹收缩,只不过似乎是转了一个角度而已. 一边长方向相对8系以速度)运动,在其前表面、侧面 和后表面分别写上F,8和R字样,四条垂直边标上1, 二、立方体的Terrell转动 2,3,4数字(见图4)。8系中的观察者直接观察该运 当我们直接观察高速运动的三雏物体时,将会看 动立方体时会看到什么情景呢?为此我们画出立方体 到十分有趣的现象,这些现象同样是光信号传递速度 的俯视图(图5),考虑到在运动方向上的长度要产生洛 的有限性和洛仑兹收缩的综合效应。V,F.Weissko pf 仑兹收缩,而与运动方向垂直的长度保持原长,所以图 ·22
可见, 表观长度是洛 仑兹 g 收缩 和光 信号传递 速度 的有 限性 ,这两个 因素联合作用的结果 ,它与洛 仑兹收缩后 的长度差 一个与 0角有关的 因子 —— ~ 一,这表 明 1一 cos0 从不同方向观察时尺子 的表观 毖度 不同, 只有当 0= 9O。时 ,表观 长度才与洛仑兹收缩公式所决定的长度相 一 致. 图 2画 出了 表观 长度 随速 度 而 变 的曲 线. 由图看出 ,随着 0角向 90。按近 ,曲线逐渐趋 近洛 仑兹收缩的 曲线. J.Terrell在 1959年 的文章中【l】, 把 系中看到 的运动尺 子的 图象等效为静止尺子的转动. 设参照系 随尺 子一起运动 ,尺子在 系中就是静止的.对尺 子上某点发 出的一束光信号来说 , 若在 系 中的传播 方向用 0角表示 (图 1或 图 3),在 系 中则应是另一 角度 0,日和 0 的关系可根据速度的洛仑兹变换求得 , 这就是大家所熟知的关于光信号传播方向的变换 式, 在我们的情形下可写成 sin日=/— 一sin (3) 卜詈coOs0 COS =—兰二一 (4)> 1一 旦cos0 从 图 3可看 出,在 系中从 口 方向上看静止 尺子时. 其宽度为 五。sin日,利用(3)式可得 0 b -Lt CO S 口sin ——_=_=——一 五o= 1一 一 毋 它正好等于在 系中从 0方 向看运动尺子时的 宽度. 于 是在 系中所观察到的运动尺子的 图象等效于 一静 止尺子 (即在 系中)转 动了 口一口角度后所看到的 图 象 .由此可见 , 系 中的观察者所看到的运动尺子并未 产生洛 仑兹 收缩 , 只不过似乎是转了一个角度而 已. 二、立方体的 Terrell转动 当我们直接观察高速运动的三维物体时, 将会看 到十分有趣的现象, 这些现象同样是光 信号传递速度 的有限性和洛仑兹收缩的综合效应.V·F·Weisskopf 圈 Z 图 3 在 1960年 的文 章 中 曾对 高 速运 动 的 立 方 俸 的 Terrell转动作过分析 ,现在我们更具体而形象地分析 这一效应. 设想有一边长的本征长度为 。的立方体 ,它沿某 一 边长方 向相对 系以速度 口运动 ,在其 前表面 、侧面 和后表面 分别写上 , 和 字样 ,四条垂直边标上 1, 2,3,4数字 (见图 4). 系中的观察者直接观察该运 动立方体时会 看到什么 情景呢? 为 此我们 画出立 方体 的俯视图(图 5),考虑到在运动方向上的长度 要产生浴 仑兹收缩 ,而 与运动方向垂直 的长度保持原 长,所 以图

r=v-ccosg c-000s0 Lo= (5) 1-0 oe0 此式表明,只要满足">ccos0,观察者就能看到后表面 的图象,其宽度r随v的增加而增大.在v=c的极限 情形下,r=L。,观察者将看到边长为工,的正方形后表 面。若)c cos 0的条件下(图5即属此情形),前 表面宽度可按推导(5)式的方法得到: -cos0 1、 -Lo c Cos0 从图看出,此时1边位于2边和4边之间,所看到的前 表面发生了反转,即看到的是反的汉字千。当→c 时,f→L。,所见前表面是边长为L的反转3的正方形, 它与正方形的后表面图象正好重合在一起。在ccos9时能同时看到后表面、侧面和 刻发出的光信号与△:时间之前4边在4位置时发出 反转3的前表面[图6(d)门,v=c时将看到重合在一起 的光信号同时到达P面,所以P面上能记录到立方体 的正方形后表面和反转3的前表面[图6(e)]. 后表面的图象(能看到字母R)。用?表示P面上记录 上面用几何关系导出的各宽度的公式都可按 到的后表面宽度,从图5的几何关系不难得到 Terrell的等效转动观点利用变换式(3)和(4)导出.观 ccos0 Lo+r cos0 察者所看到的运动立方体的图象可等效为静止立方体 cos 的转动。在)=c时,相当于静止立方体转动了-0的 角度(参见图5),并且看起来似乎是透明的。 即 (下转12页) ·23=
运 动 方 向 图 4 中把立方体画成了长方体. 需要再次指出,长方体反 映 了运动立方体本身在 系中的空 间特征, 丝毫也不 是 系中的观察者所看到的实际形象. 我们依然假定 观 察面 P离 立方 体足够远 , 使到达P面的光都近乎 垂 直 入射 ;观察方 向仍用 0角表示. 图 5是按 =0.8D, 0---60。的 情形 画的. 图 5 现来讨论观 察面 p上记录至B的 图象. 3边在 某时 亥Ⅱ发 出的光 信号与 △t时 间之前 4边在 4 位置时发 出 的光信号同时到达P面, 所以P面上能记录到立方体 后 表面的图象(能看到字母R). 用 r表示 P面上记录 到的后 表面宽度 ,从 图 5的几何关 系不难得到 即 cCOS0 一 o + rCOS0 十击 r = C一 60S 此式表明 ,只要满足 2,>CCOS0,观察者就 能看 到后表面 的图象 ,其宽度 r随 的增加而 增大. 在 =c的极限 情形下,r=L。,观察者将看到边长为 二。的正方形后表 面. 若 cCOS0的条件下(图 5即属此情形),前 表面宽度 ,可按推导(5)式 的方法得到· … - - COS0(~ 1一 ÷ os 厶 从 图看出 ,此时 l边位于 2边和 4边之 闻,所看到 的前 表面 发生 了反转, 即看到的是 反的 汉字丁 . 当 口+o 时 ,产 所见前表面是 边长为工。的反转 3的正方形, 它与正方形的后表 面图 象正 好重 合在 一起. 在口eCOS0时能同时看到后表面 、侧面和 反转 3的前表面[图 6()]; =c时将看到重合在一起 的正方形后表面和反转 3的前表面[图 6(e)]. 上面用 几何 关系 导 出 的各 宽度 的公 式都 可 按 Terrell的等效转动观点利用变换式 (3)和(4)导出. 观 察者所看到的运动立方体的图象可等效为静止立 方体 的转动.在 =c时 ,相 当于静止立方体转动了 一口的 角度 (参见 图 5),并且看起来 似乎是透 明的. (下转 12页) · 23 · 口 一甜 卜 ll

y2+22=k2+2kx (17) 因此(21)式可化简成 或 红=6(g+2-创 (18) 0= 0o vk (23) V2√k+x 现在求它的总曲率K,由于曲面方程(18)具有 x=∫(y,)的形式,因此(3)式中的卫应改为 比较(19)和(23)式.得g=o√EK (24) 6x 0¥ ,9应改为号,等等,即 这就是所要求的关系式。 六,讨论 卫 0x=名, 02=R,q= 0x=y (1)本文所分析的三种二次曲面的电荷面 0y k y=02x=1 密度0都与曲面的总曲率K的1/4次幂成正 6x1 =02江=友,=0y产=市 比,这表明曲率大的地方电荷密度也大,与实 的6=0 验规律一致。由于总曲率与主曲率半径R,和 8=0z0y R2的乘积成反比,因此粗略地讲,对于这几种 代入(3)式,并利用(17)式,得 形状的导体电荷密度与曲率半径R的平方根成 2 1 反比,这与[6]所得的结论(σ与R成反比)不 K=2+y产+2=4(k+0)产 (19) 同。 已知带电旋转抛物面电场的电势为4幻 (2)本文所得结论并不具有普遍适用性, =2 xook In=a+y+y 这可从下述事实看出,第一,对于带电平面,柱 (20) 面及锥面,其总曲率K显然等于零,而电荷密 式中为顶点(-会,0,0)处电荷面密度。 度却不为零,也不为常数:第二,导体表面凹进 去的部份(曲率为负)电荷密度最小。这两件事 由关系式。= E=1,v1上,可得 实本文均不能加以解释,对其它形状的导体是 4π4元 否仍有类似关系亦需进一步讨论。 V 2 gok 参考文献 2(-出+Vx2+y2+22)m [1了W.R.斯迈斯著,戴世强译,静电学和电动力学,科学出 1 版社,1981,上册,第五章, ×(2+y2+2 (21) [2]曹国良,孤立带电导体的拉普拉斯方程解,物理,1982,1, 第59页. 注意到旋转抛物面的曲面方程(17)可表示为 C3]数学手册,人民教育出版社,1979年,第七章 [4]福里斯等著,普通物理学,1954年,第一卷,第九章。 -x+/x2+y2+22=k(x<0)(22) [5]曹萱龄等编,物與学,1979年中册,第65页. (上接23页) (a)0=0s4c.(b)t=0.6c (c)v=cos0 (d)0=0.8g (e)v=c 8=45 图6 总之,高速运动物体的洛仑兹收缩效应是不能直 参考。文献 接看到的。以上例子或许有助于消除由一般教科书中 通常采用的表述方法所引起的错觉. C1]J.Terrell,Py.Reo.116(1959),1041.' [2]V.F.Weisskopf,Phy.Today,13(Sep.1960),24. ·12·
3,+ =k+2kx (17) 因此(21)式可化简成 或 :=:-2-~-(y+。一k。) (18) 现在求它的总曲率K.由于曲面方程(18)具有 = f(Y,)的 形式 ,因此 (3)式 中 的 应 改 为 鲁,g应改为 ,等等,印 Ox 名 Ox i, 百 00 1 . 00 1 r:= 一 百 , 百 s= = 。 代入(3)式,并利用(17)式 ,得 =可 = (19) 已知 带 电旋转 抛物面 电场 的 电势为m = 2~ ok In —- x— +— Cx2—~ y~ 2+ z2 (2O) 式中。为顶点(一睾,o,o)处电荷面密度. 由关系式 一彳,_=:1l l曲面上,可得 o-:==_ _ l/'Y aok 2(一 +1//。。 干 i‘), ×百 (21) 注意到旋转抛物面的曲面方程(17)可表示为 一茹+1// _ - :庇( < O) (22) : 粤 : (23) 1/ 2 i/ k+ 一 一 1 比较 (19)和 (23)式 .得 O'~-- 01/ (24) 这就是所要求的关系式. 六 讨 论 (1)本文所分析的三种二次曲面的电荷面 密度 都与曲面的总曲率 的 1/4次幂 成 正 比 ,这 表 明曲率 大的 地方 电荷密度 也 大 ,与实 验规律一致 .由于总曲率与主曲率半 径 和 的乘积成反 比,因此粗略地讲,对于这几种 形状的导体电荷密度与曲率半径 的平方根成 反 比 ,这 与 [6]所 得的结 论 ( 与 成反 比)不 同。 (2)本文所得结论并不具有普遍适用性, 这可从下述事实看出,第一,对于带电平面 ,柱 面及锥面 ,其总曲率 显然等于零,而电荷密 度却不为零,也不为常数,第=,导体表面凹进 去的部份(曲率为负)电荷密度最小.这两件事 实本文均不能加以解释,对其它形状的导体是 否仍有类似关系亦需进一步讨论. 参 考 文 献 【1]W.R.斯迈斯著 ,戴世强译 ,静 电学和 电动力 学 ,科学 出 版社 ,1981,上册 ,第五章. [2]曹国良,孤立带 电导体的拉普拉斯方程解 ,物理 ,1982,1, 第 59页. C3j数学手册 ,人 民教育出版社,1979年 ,第七章. [4]福里斯等著,普通物理学,1954年 ,第一卷,第九氧 【6]曹萱龄等编 ,物理学,1979年中册 ,第 65页. (上 按 23页 ) 3 2 1 3 2 囤I. 一 41~3,2 总之。 高速运动物体的洛 仑兹收缩效应是不能直 接看 到的. 以上例子或许有助于消除由一般教科 书中 通常采用 的表述方法所引起的错觉. · I2 · 参 考 文 献 C1]J.Terrell,Phy.Bey.116(1959),1041.. [2]V.F.Weisskopf。Phy。~oday,13(Sep.1960),24.