
第五章 多组元系统、化学平衡 5.1多组元单相系统 5.2理想混合气体和理想混合物 5.3多元复相系统 5.4多元复相平衡条件 5.5 Gibbs相律例子 5.6多元复相系统的例子 5.7化学平衡
第五章 多组元系统、化学平衡 5.1 多组元单相系统 5.2 理想混合气体和理想混合物 5.3 多元复相系统 5.4 多元复相平衡条件 5.5 Gibbs 相律例子 5.6 多元复相系统的例子 5.7 化学平衡

5.1多组元单相系统 参量 均匀的、含有k个组元的系统 Q原始参量 热学参量:T;力学参量:p:几何参量:V:: 化学参量:N1,N2,·,Nk 或者:T,p,V,M=N1m1,M2=N2m2,·,Mk=Nkmk Ni:i-th组元的摩尔数:m:i-th组元的原子量 Q高级参量 内能U,熵S,自由能F,Gibbs自由能G,· U=U(S,V,N1,N2,·,Nk) F=F(T,V,N1,N2,...,Nk)=U-TS G=G(T,p,N1,N2,..,Nk)=F+pV
5.1 多组元单相系统 参量 均匀的、含有 𝑘 个组元的系统 原始参量 热学参量:T;力学参量:p;几何参量:V;· · · ; 化学参量:𝑁1, 𝑁2, · · · , 𝑁𝑘 或者:T, p, V, 𝑀1 = 𝑁1𝑚1, 𝑀2 = 𝑁2𝑚2, · · · , 𝑀𝑘 = 𝑁𝑘𝑚𝑘 𝑁𝑖:𝑖-th 组元的摩尔数;𝑚𝑖:𝑖-th 组元的原子量 高级参量 内能 U,熵 S,自由能 F,Gibbs 自由能 G,· · · 𝑈 = 𝑈(𝑆, 𝑉, 𝑁1, 𝑁2, · · · , 𝑁𝑘 ) 𝐹 = 𝐹(𝑇, 𝑉, 𝑁1, 𝑁2, · · · , 𝑁𝑘 ) = 𝑈 − 𝑇 𝑆 𝐺 = 𝐺(𝑇, 𝑝, 𝑁1, 𝑁2, · · · , 𝑁𝑘 ) = 𝐹 + 𝑝𝑉

化学势 dU=TdS-pdV+μ1dN1+2dN2+…HRdNk T=T(S,V,N1,...,Nk)=T(S,V,{Ni}) D=pSw》=Ns, /a0 41=41(S,V,N1,N2,…,Nk)= 00 =(aNs,V,d =4(s.v》=(照)s
化学势 𝑑𝑈 = 𝑇 𝑑𝑆 − 𝑝𝑑𝑉 + 𝜇1𝑑𝑁1 + 𝜇2𝑑𝑁2 + · · · 𝜇𝑘𝑑𝑁𝑘 𝑇 = 𝑇 (𝑆, 𝑉, 𝑁1, · · · , 𝑁𝑘 ) = 𝑇 (𝑆, 𝑉, {𝑁𝑖}) = ( 𝜕𝑈 𝜕𝑆 ) 𝑉 ,𝑁1,𝑁2,··· ,𝑁𝑘 = ( 𝜕𝑈 𝜕𝑆 ) 𝑉 {𝑁𝑖 } 𝑝 = 𝑝(𝑆, 𝑉, {𝑁𝑖}) = ( 𝜕𝑈 𝜕𝑉 ) 𝑆, {𝑁𝑖 } 𝜇1 = 𝜇1 (𝑆, 𝑉, 𝑁1, 𝑁2, · · · , 𝑁𝑘 ) = ( 𝜕𝑈 𝜕𝑁1 ) 𝑆,𝑉 ,𝑁2,··· ,𝑁𝑘 = ( 𝜕𝑈 𝜕𝑁1 ) 𝑆,𝑉 , {𝑁𝑖≠1 } 𝜇𝑖 = 𝜇𝑖(𝑆, 𝑉, {𝑁𝑗 }) = ( 𝜕𝑈 𝜕𝑁𝑖 ) 𝑆,𝑉 , {𝑁𝑗≠𝑖 }

化学势 F=F(T,V,{Ni}) dF=-Sar-pdw+∑:dW s=T,v.W》=-w 4=4(T,V,{N)= G=G(T,p,{Ni}) dG=-Sdar+Vdp+∑AdN 5=sT,P.w》=-9)p =(T,p,{W)=
化学势 𝐹 = 𝐹(𝑇, 𝑉, {𝑁𝑖}) 𝑑𝐹 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 𝑆 = 𝑆(𝑇, 𝑉, {𝑁𝑖}) = − ( 𝜕𝐹 𝜕𝑇 ) 𝑉 {𝑁𝑖 } 𝜇𝑖 = 𝜇(𝑇, 𝑉, {𝑁𝑖}) = ( 𝜕𝐹 𝜕𝑁𝑖 ) 𝑇 𝑉 {𝑁𝑗≠𝑖 } 𝐺 = 𝐺(𝑇, 𝑝, {𝑁𝑖}) 𝑑𝐺 = −𝑆𝑑𝑇 + 𝑉 𝑑𝑝 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 𝑆 = 𝑆(𝑇, 𝑝, {𝑁𝑖}) = − ( 𝜕𝐺 𝜕𝑇 ) 𝑝{𝑁𝑖 } 𝜇𝑖 = 𝜇𝑖(𝑇, 𝑝, {𝑁𝑖}) = ( 𝜕𝐺 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑗≠𝑖 }

Maxwell关系 aF=-sdr-pdw+∑dw 化学势随温度的改变 化学势随体积的改变 组元会影响其他组元
Maxwell 关系 𝑑𝐹 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 ( 𝜕𝑆 𝜕𝑉 ) 𝑇 {𝑁𝑖 } = ( 𝜕 𝑝 𝜕𝑇 ) 𝑉 {𝑁𝑖 } ( 𝜕𝑆 𝜕𝑁𝑖 ) 𝑇 𝑉 {𝑁𝑗≠𝑖 } = − ( 𝜕𝜇𝑖 𝜕𝑇 ) 𝑉 {𝑁𝑗 } ✞ ✝ ☎ 化学势随温度的改变 ✆ ( 𝜕 𝑝 𝜕𝑁𝑖 ) 𝑇 𝑉 {𝑁𝑗≠𝑖 } = − ( 𝜕𝜇𝑖 𝜕𝑉 ) 𝑇 {𝑁𝑗 } ✞ ✝ ☎ 化学势随体积的改变 ✆ ( 𝜕𝜇𝑖 𝜕𝑁𝑗 ) 𝑇 𝑉 {𝑁𝑘≠𝑗 } = ( 𝜕𝜇𝑗 𝜕𝑁𝑖 ) 𝑇 𝑉 {𝑁𝑘≠𝑖 } ✞ ✝ ☎ 组元会影响其他组元 ✆

Maxwell关系 dG=-Sdr+Vdp+∑dN 化学势随温度的改变 84y ap ) 化学势随压强的改变 畿 组元会影响其他组元
Maxwell 关系 𝑑𝐺 = −𝑆𝑑𝑇 + 𝑉 𝑑𝑝 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 ( 𝜕𝑆 𝜕 𝑝 ) 𝑇 {𝑁𝑖 } = − ( 𝜕𝑉 𝜕𝑇 ) 𝑝{𝑁𝑖 } ( 𝜕𝑆 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑗≠𝑖 } = − ( 𝜕𝜇𝑖 𝜕𝑇 ) 𝑝{𝑁𝑗 } ✞ ✝ ☎ 化学势随温度的改变 ✆ ( 𝜕𝑉 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑗≠𝑖 } = ( 𝜕𝜇𝑖 𝜕 𝑝 ) 𝑇 {𝑁𝑗 } ✞ ✝ ☎ 化学势随压强的改变 ✆ ( 𝜕𝜇𝑖 𝜕𝑁𝑗 ) 𝑇 𝑝{𝑁𝑘≠𝑗 } = ( 𝜕𝜇𝑗 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑘≠𝑖 } ✞ ✝ ☎ 组元会影响其他组元 ✆

Gibbs-.Duhem关系 单组元 G(T,p,N)=Ng(T,p)=Nu(T,p) N=N1+++M=∑N u=Ts-pv+8=Ts-ps+u xi Ni/N ∑= k-1个强度量+一个广延量N U=Nu S=Ns V=Nv... U=U(Ns,Nv,{Nxi})=Nu(s,v,{xi}) dU Ndu udN =Tds-paW+∑dw =NTds-Npd+N∑aidi+(Ts-pv+∑xi)dN W=u(s,》=Ts-pv+∑: Gibbs-Duhem关系 du Tds-pdv ∑4d, 仍把x看成k个独立变量 霉考虑强度量时,总摩尔数N起的作用并不大一冗余参数
Gibbs-Duhem 关系 𝑁 = 𝑁1 + 𝑁2 + · · · + 𝑁𝑘 = ∑ 𝑖 𝑁𝑖 𝑥𝑖 = 𝑁𝑖/𝑁 ∑ 𝑖 𝑥𝑖 = 1 ☞ ✞ ✝ ☎ ✆ 𝑘 − 1 个强度量 + 一个广延量 𝑁 𝑈 = 𝑁𝑢 𝑆 = 𝑁 𝑠 𝑉 = 𝑁𝑣 · · · 𝑈 = 𝑈(𝑁 𝑠, 𝑁𝑣, {𝑁𝑥𝑖}) = 𝑁𝑢(𝑠, 𝑣, {𝑥𝑖}) 𝑑𝑈 = 𝑁 𝑑𝑢 + 𝑢𝑑𝑁 = 𝑇 𝑑𝑆 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 = 𝑁𝑇 𝑑𝑠 − 𝑁 𝑝𝑑𝑣 + 𝑁 ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 + (𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖)𝑑𝑁 𝑢 = 𝑢(𝑠, 𝑣, {𝑥𝑖}) = 𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖 ☞ ✞ ✝ ☎ ✆ Gibbs-Duhem 关系 𝑑𝑢 = 𝑇 𝑑𝑠 − 𝑝𝑑𝑣 + ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 ☞ ✞ ✝ ☎ 仍把 ✆ 𝑥𝑖 看成 𝑘 个独立变量 ☞考虑强度量时,总摩尔数 𝑁 起的作用并不大 ⇒ 冗余参数。 ✗ ✖ ✔ ✕ 单组元 𝐺(𝑇, 𝑝, 𝑁) = 𝑁𝑔(𝑇, 𝑝) = 𝑁 𝜇(𝑇, 𝑝) 𝑢 = 𝑇 𝑠 − 𝑝𝑣 + 𝑔 = 𝑇 𝑠 − 𝑝𝑠 + 𝜇

Gibbs-Duhem关系 M=Ts-pv+∑x4 d=Tds-pdw+∑hd U=TS-pV+∑NMw G=G(T,p.{)=U-TS+pV=∑N4=N∑x,T,p,) 8=8(T,p,xi)=G/N=∑x s=r+咖+∑4 ∑:x=1,只有k-1个独立的x Maxwell关系
Gibbs-Duhem 关系 𝑢 = 𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖 𝑑𝑢 = 𝑇 𝑑𝑠 − 𝑝𝑑𝑣 + ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 𝑈 = 𝑇 𝑆 − 𝑝𝑉 + ∑ 𝑖 𝑁𝑖𝜇𝑖 𝐺 = 𝐺(𝑇, 𝑝, {𝑁𝑖}) = 𝑈 − 𝑇 𝑆 + 𝑝𝑉 = ∑ 𝑖 𝑁𝑖𝜇𝑖 = 𝑁 ∑ 𝑖 𝑥𝑖𝜇𝑖(𝑇, 𝑝, {𝑥𝑖}) 𝑔 = 𝑔(𝑇, 𝑝, {𝑥𝑖}) = 𝐺/𝑁 = ∑ 𝑖 𝑥𝑖𝜇𝑖 𝑑𝑔 = −𝑠𝑑𝑇 + 𝑣𝑑𝑝 + ∑ 𝑘 𝑖=1 𝜇𝑖𝑑𝑥𝑖 ✞ ✝ ☎ ✆ ∑ 𝑖 𝑥𝑖 = 1,只有 𝑘 − 1 个独立的 𝑥𝑖 Maxwell 关系 ( 𝜕𝑠 𝜕 𝑝 ) {𝑥𝑖 } = − ( 𝜕𝑣 𝜕𝑇 ) {𝑥𝑖 } ( 𝜕𝜇𝑖 𝜕𝑥 𝑗 ) 𝑇 𝑝{𝑥𝑘≠𝑗 } = ( 𝜕𝜇𝑗 𝜕𝑥𝑖 ) 𝑇 𝑝{𝑥𝑘≠𝑖 } · · ·

巨势 J=JT,V,》=F-∑N dF=-SdT-pdW+∑hdN, dW=-sdr-pdW-∑N,d, J=F->Niui=F-G=F-(F+pV)=-pV =-p(T,V,{4})V 这里的压强是以温度、体积和化学势为自变量,和普通状态 方程不同。例如从理想气体的状态方程J=-pV=-NRT= -N(T,V,)RT并不包含所有热力学性质。 露巨势主要用于处理和粒子源接触的系统 统计物理中巨势可以用巨正则系综计算
巨势 𝐽 = 𝐽 (𝑇, 𝑉, {𝜇𝑖}) = 𝐹 − ∑ 𝑖 𝑁𝑖𝜇𝑖 𝑑𝐹 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 𝑑𝐽 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 − ∑ 𝑖 𝑁𝑖𝑑𝜇𝑖 𝐽 = 𝐹 − ∑ 𝑖 𝑁𝑖𝜇𝑖 = 𝐹 − 𝐺 = 𝐹 − (𝐹 + 𝑝𝑉) = −𝑝𝑉 = −𝑝(𝑇, 𝑉, {𝜇𝑖})𝑉 ☞ 这里的压强是以温度、体积和化学势为自变量,和普通状态 方程不同。例如从理想气体的状态方程 𝐽 = −𝑝𝑉 = −𝑁 𝑅𝑇 = −𝑁(𝑇, 𝑉, 𝜇)𝑅𝑇 并不包含所有热力学性质。 ☞ 巨势主要用于处理和粒子源接触的系统 ☞ 统计物理中巨势可以用巨正则系综计算
5.2 混合理想气体 k个组元,N1,=Nx1,N2=Nx2,·,Nk=Nxk,N=∑iNi,x= Ni/N pVi=NiRT 分体积定律 P(∑)=pV=(∑NM)Rr=NRI PiV NiRT 分压定律 p-2m=∑-∑:
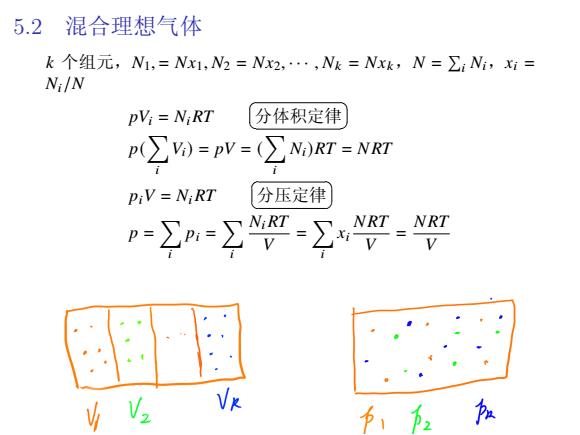
5.2 混合理想气体 𝑘 个组元,𝑁1, = 𝑁𝑥1, 𝑁2 = 𝑁𝑥2, · · · , 𝑁𝑘 = 𝑁𝑥𝑘,𝑁 = ∑ 𝑖 𝑁𝑖,𝑥𝑖 = 𝑁𝑖/𝑁 𝑝𝑉𝑖 = 𝑁𝑖𝑅𝑇 ✞ ✝ ☎ 分体积定律 ✆ 𝑝( ∑ 𝑖 𝑉𝑖) = 𝑝𝑉 = ( ∑ 𝑖 𝑁𝑖)𝑅𝑇 = 𝑁 𝑅𝑇 𝑝𝑖𝑉 = 𝑁𝑖𝑅𝑇 ✞ ✝ ☎ 分压定律 ✆ 𝑝 = ∑ 𝑖 𝑝𝑖 = ∑ 𝑖 𝑁𝑖𝑅𝑇 𝑉 = ∑ 𝑖 𝑥𝑖 𝑁 𝑅𝑇 𝑉 = 𝑁 𝑅𝑇 𝑉