
第一章引言、热力学第一定律 1.1 Introduction 1.2温度:热力学第零定律 1.3过程 1.4热力学第一定律 1.5功的表达式 1.6热容 1.7理想气体的Carnot过程
第一章 引言、热力学第一定律 1.1 Introduction 1.2 温度:热力学第零定律 1.3 过程 1.4 热力学第一定律 1.5 功的表达式 1.6 热容 1.7 理想气体的 Carnot 过程

1.1 Introduction 科研第一步:把宇宙分为系统和环境 a系统(system) 研究对象,通常指占据某个特定空间内的东西 Q环境/外界(environment/surrounding) 宇宙中对象之外的其它部分 界面/约束(constrain/wall/surface/interface) 把对象和环境区分开来,可以是实体的、也可以是虚拟的 Surrounding 有人把宇宙可以分为系统和 环境这个假设戏称为热力学 第负无穷大定律。 System 霉传统的热力学里系统和环境 只能在界面相互作用→只考 虑短程相互作用。 Interface
1.1 Introduction 科研第一步:把宇宙分为系统和环境 系统(system) 研究对象,通常指占据某个特定空间内的东西 环境/外界(environment/surrounding) 宇宙中对象之外的其它部分 界面/约束(constrain/wall/surface/interface) 把对象和环境区分开来,可以是实体的、也可以是虚拟的 ✬ ✫ ✩ ✪ ☞有人把宇宙可以分为系统和 环境这个假设戏称为热力学 第负无穷大定律。 ☞传统的热力学里系统和环境 只能在界面相互作用 ⇒ 只考 虑短程相互作用

系统的分类 按照边界/界面的不同把系统分类:典型的三类系统 。孤立系统 固定的边界,不可变形,不可传递能量和物质 系统和环境所有性质都不接触 内外所有的平衡均可不同 Q封闭系统 边界可以变形,可以传递能量,但不能传递物质 可以有力(包括电磁力)、热接触,但是无化学接触 内外可以达到力学、热学平衡,但是可以化学不平衡 Q开放系统 边界可以变形,可以传递能量和物质 具有所有可能的力、热和化学接触 内外达到所有平衡:力学、热学和化学平衡 霉存在介乎中间的系统 介乎孤立/封闭系统:边界可以是刚性透热,或者弹性绝热的 介乎封闭/开放系统:半透膜,只有部分物质可以实现化学接触
系统的分类 按照边界/界面的不同把系统分类:典型的三类系统 孤立系统 固定的边界,不可变形,不可传递能量和物质 系统和环境所有性质都不接触 内外所有的平衡均可不同 封闭系统 边界可以变形,可以传递能量,但不能传递物质 可以有力(包括电磁力)、热接触,但是无化学接触 内外可以达到力学、热学平衡,但是可以化学不平衡 开放系统 边界可以变形,可以传递能量和物质 具有所有可能的力、热和化学接触 内外达到所有平衡:力学、热学和化学平衡 ☞ 存在介乎中间的系统 介乎孤立/封闭系统:边界可以是刚性透热,或者弹性绝热的 介乎封闭/开放系统:半透膜,只有部分物质可以实现化学接触
系统→模型 对象具有非常多的性质,但是在研究的时候不可能,也没有必要 研究所有的性质⑧对研究对象进行抽象和理想化,建立模型,只 留下理想的性质 色彩、纹路 气味、味道 系统 力学性质 模型 性质 电磁性质 性质 尺寸 化学性质
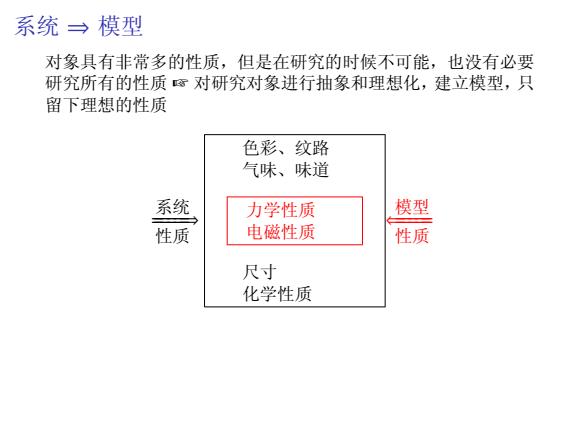
系统 ⇒ 模型 对象具有非常多的性质,但是在研究的时候不可能,也没有必要 研究所有的性质 ☞ 对研究对象进行抽象和理想化,建立模型,只 留下理想的性质 系统 ======⇒ 性质 色彩、纹路 气味、味道 力学性质 电磁性质 尺寸 化学性质 模型 ⇐====== 性质

描述系统/模型:参量 选定参量来描述模型的性质与关系 原始参量(primitive parameters):直观,与感官系统直接 相联系的性质 例如:位置r:时间t:速度v:质量m:力F:电量Q 关系:r=r0+v1,F=Q1Q2r/(0r3), Q高级参量(secondary parameters):抽象,对原始参量的数 学组合 例如:加速度a=光;动量p=mv:动能K=mv2/2:势 能U=mgh 关系:牛顿定律F=ma,能量守恒K+U三C 哈密顿量H=H(r,p),正则方程产=VpH,p=-VrH 露高级参量一抽象化一简化列方程一更广泛的规律
描述系统/模型:参量 选定参量来描述模型的性质与关系 原始参量(primitive parameters): 直观,与感官系统直接 相联系的性质 例如:位置 𝒓;时间 t;速度 𝒗;质量 𝑚;力 𝑭;电量 𝑄 关系:𝒓 = 𝒓0 + 𝒗𝑡,𝑭 = 𝑄1𝑄2 𝒓/(𝜀0𝑟 3 ),· · · 高级参量(secondary parameters):抽象,对原始参量的数 学组合 例如:加速度 𝒂 = 𝑑𝒗 𝑑𝑡 ;动量 𝒑 = 𝑚𝒗;动能 𝐾 = 𝑚𝑣2 /2;势 能 𝑈 = 𝑚𝑔ℎ 关系:牛顿定律 𝑭 = 𝑚𝒂,能量守恒 𝐾 + 𝑈 ≡ 𝐶 · · · 哈密顿量 𝐻 = 𝐻(𝒓, 𝒑),正则方程 𝒓¤ = ∇ 𝒑𝐻, 𝒑¤ = −∇𝒓𝐻 ☞ 高级参量 ⇒ 抽象化 ⇒ 简化列方程 ⇒ 更广泛的规律

不同分支里的模型 几何参量V,时间t 学科 模型 参数 规律 质点,刚 位置r,速度v,力F r=vt 力 体,理想 加速度a,动量p F =ma=p 学 弹性体, 动能K、势能U E=K+U三C 理想流体 哈密顿量H p=-0rH 压强P r=OpH 电 点电荷, 电量Q,电流1,磁矩M 库伦定律 磁 磁偶极 电磁场强度,电位移矢量 Maxwell方程 学 矩,电磁 电磁场能、动量 E-ED+BH 2 介质 哈密顿量H p=-0rH 化学 化学组元 物质的量,摩尔数 化学反应式 N2,H2 nN,,nH N2+3H2 =2NH3 热力学 温度T,内能U,熵S 状态方程 热力学 平衡态、 自由能F,Gibbs自由能G 热力学三定律 准静态过 化学势4 程
不同分支里的模型 几何参量 𝑉,时间 𝑡 学科 模型 参数 规律 力 学 质点,刚 体,理想 弹 性 体, 理想流体 位置 𝒓, 速度 𝒗,力 𝑭 𝒓 = 𝒗𝑡 加速度 𝒂,动量 𝒑 𝑭 = 𝑚𝒂 = 𝒑¤ 动能 𝐾、势能 𝑈 𝐸 = 𝐾 + 𝑈 ≡ 𝐶 哈密顿量 𝐻 𝒑¤ = −𝜕𝒓𝐻 压强 𝑝 𝒓¤ = 𝜕𝒑𝐻 电 磁 学 点 电 荷, 磁 偶 极 矩,电磁 介质 电量 𝑄,电流 𝐼,磁矩 𝑴 库伦定律 电磁场强度,电位移矢量 Maxwell 方程 电磁场能、动量 𝐸 = 𝑬·𝑫 2 + 𝑩·𝑯 2 哈密顿量 𝐻 𝒑¤ = −𝜕𝒓𝐻 化学 化学组元 物质的量,摩尔数 化学反应式 𝑁2, 𝐻2 𝑛𝑁2,𝑛𝐻2 𝑁2 + 3𝐻2 = 2𝑁𝐻3 热力学 热 力 学 平 衡 态、 准静态过 程 温度 𝑇,内能 𝑈,熵 𝑆 状态方程 自由能 𝐹,Gibbs 自由能 𝐺 热力学三定律 化学势 𝜇

热力学系统和热力学参量 。热力学的研究对象:热力学系统 处于热力学平衡态下的宏观体系,包含大量的微观粒子 霉N个粒子的系统一般情况下需要6N个参数描述系统状 态~1023个参数 Q热力学平衡态 在外界约束不改变时,系统通过足够长时间的演化后达到的 一种状态,在此状态下各个宏观参量不发生改变 露可以只用少数几个宏观参量就可以描述系统—— 热力学 参量 ⑧热力学平衡态是热力学中的第一个模型 Q多长算是足够长? 。哪些参量是宏观参量?
热力学系统和热力学参量 热力学的研究对象:热力学系统 处于热力学平衡态下的宏观体系,包含大量的微观粒子 ☞ 𝑁 个粒子的系统一般情况下需要 6𝑁 个参数描述系统状 态 ∼ 1023 个参数 热力学平衡态 在外界约束不改变时,系统通过足够长时间的演化后达到的 一种状态,在此状态下各个宏观参量不发生改变 ☞ 可以只用少数几个宏观参量就可以描述系统——–热力学 参量 ☞ 热力学平衡态是热力学中的第一个模型 多长算是足够长? 哪些参量是宏观参量?

热力学系统和热力学参量 。热力学参量:宏观参量 Q几何参量:形状、尺寸、表面积A,体积V,… Q力学参量:张力F,压强p,… 动能K,势能U,Hamiltonian H, o. 电磁学参量:电场E,电偶极矩P,电位移矢量D=soEV+P: 磁场H,磁偶极矩M,磁感应强度B=4o(HB+M):· 电磁能E=E·D/2+B·H/2,Hamiltonian H,· Q化学参量:物质的量NA,NB,· 反应热,化学势HA,μB, Q热学参量:温度T 内能U,熵S,自由能F,焓H,Gibbs自由能G 霉平衡态热力学力不包含时间参量 露热力学参量是宏观物理量,是微观物理量的总和或者平均, 忽略了大量微观细节
热力学系统和热力学参量 热力学参量:宏观参量 几何参量:形状、尺寸、表面积 𝐴,体积 𝑉,· · · 力学参量:张力 𝐹,压强 𝑝,· · · 动能 𝐾,势能 𝑈,Hamiltonian 𝐻,· · · 电磁学参量:电场 𝑬,电偶极矩 𝑷,电位移矢量 𝑫 = 𝜀0𝑬𝑉 +𝑷; 磁场 𝑯,磁偶极矩 𝑴,磁感应强度 𝑩 = 𝜇0 (𝑯𝐵 + 𝑴);· · · 电磁能 𝐸 = 𝑬 · 𝑫/2 + 𝑩 · 𝑯/2,Hamiltonian 𝐻,· · · 化学参量:物质的量 𝑁𝐴,𝑁𝐵,· · · 反应热,化学势 𝜇𝐴,𝜇𝐵,· · · 热学参量:温度 𝑇 内能 𝑈,熵 𝑆,自由能 𝐹,焓 𝐻,Gibbs 自由能 𝐺 · · · ☞ 平衡态热力学力不包含时间参量 ☞ 热力学参量是宏观物理量,是微观物理量的总和或者平均, 忽略了大量微观细节

热力学参量的分类 热力学平衡态下,按照参量和粒子数N(或者摩尔数n=N/NA) 的关系,可以分为两类 Q广延量:与粒子数成正比,心N1 例如:总质量M,总体积V,内能U,… Q强度量:与粒子数无关,cxN0 例如:压强p,温度T,电磁场E,H, 传统热力学参量只有这两种,要么心N,要么心W,不会 有其它类型(如xN2)的参量。 s非平衡参量可以既非广延量也非强度量,例如涨落心N12 广延量和强度量可以互相转化:u=U/N,orU/W ⑧能够把物理量划分为广延量和强度量的条件是相互作用是短 程的。这样把大系统划分成小系统时,只要考虑小系统之间 界面的影响。在系统很大时(热力学极限),界面的影响相 对可以忽略,大系统可以看成是小系统的简单叠加。如果有 长程作用(例如重力)的话,就不能这么简单处理。这种系 统称为非广延系统,典型例子包括星系等
热力学参量的分类 热力学平衡态下,按照参量和粒子数 𝑁(或者摩尔数 𝑛 = 𝑁/𝑁𝐴) 的关系,可以分为两类 广延量:与粒子数成正比,∝ 𝑁 1 例如:总质量 𝑀,总体积 𝑉,内能 𝑈,· · · 强度量:与粒子数无关,∝ 𝑁 0 例如:压强 𝑝,温度 𝑇,电磁场 𝑬, 𝑯,· · · ☞ 传统热力学参量只有这两种,要么 ∝ 𝑁 1,要么 ∝ 𝑁 0,不会 有其它类型(如 ∝ 𝑁 1/2)的参量。 ☞ 非平衡参量可以既非广延量也非强度量,例如涨落 ∝ 𝑁 ±1/2 ☞ 广延量和强度量可以互相转化:𝑢 = 𝑈/𝑁,or 𝑈/𝑉 ☞ 能够把物理量划分为广延量和强度量的条件是相互作用是短 程的。这样把大系统划分成小系统时,只要考虑小系统之间 界面的影响。在系统很大时(热力学极限),界面的影响相 对可以忽略,大系统可以看成是小系统的简单叠加。如果有 长程作用(例如重力)的话,就不能这么简单处理。这种系 统称为非广延系统,典型例子包括星系等

热力学的特点和难点 。描述宏观性质、宏观参量之间的关系,与微观细节无关 ·可以同时考虑多种性质,其规律是普适的 不管系统多复杂,需要多少个参量描述, 只要处于热力学平衡态,热力学规律都成立
热力学的特点和难点 描述宏观性质、宏观参量之间的关系,与微观细节无关 可以同时考虑多种性质,其规律是普适的 不管系统多复杂,需要多少个参量描述, 只要处于热力学平衡态,热力学规律都成立