第5章地基中的应力计算 5.1概述 引起地基土的变形, 导致建筑物的沉降、倾 斜或水平位移。 土体中应力 状态发生变化 当应力超过地基土 的强度时,地基就会因 丧失稳定性而破坏,造 成建筑物倒塌。 土质学与土力学 55-1 吉林大学建设工程学院
土质学与土力学 55—1 吉林大学建设工程学院 土体中应力 状态发生变化 引起地基土的变形, 导致 建筑物的沉降、倾 斜或水平位移。 当应力超过地基土 的强度时,地基就会因 丧失稳定性而破坏,造 成建筑物倒塌。 5.1 概述

第5章地基中的应力计算 应力计算的基本假设: 1.假设地基土为连续、均匀、各向同性、半无限的线弹性体 2.弹性理论。 土中的应力按引起的原因可分为: 由土本身有效自重在地基内部引起的自重应力; 由外荷(静荷载或动荷载)在地基内部引起的附加应力。 土质学与土力学 55-2 吉林大学建设工程学院
土质学与土力学 55—2 吉林大学建设工程学院 土中的应力按引起的原因可分为: 由土本身有效自重在地基内部引起的自重应力; 由外荷(静荷载或动荷载) 在地基内部引起的附加应力。 应力计算的基本假设: 1.假设地基土为连续、均匀、各向同性、半无限的线弹性体 2.弹性理论

第5章地基中的应力计算 5.2土中自重应力 研究目的:确定土体的初始应力状态 研究方法:土体简化为连续体,应用连续体力学(例如弹性力学)方法来 研究土中应力的分布。 假设天然土体是一个半无限体,地面以下土质均匀,天然重度为Y (kN/m),则在天然地面下任意深度z(m)处的竖向自重应力oc(kPa),可 取作用于该深度水平面上任一单位面积上土柱的重量?x计算,即: Ocz=YZ σz沿水平面均匀分布,且与2成正比,即随深度增加而增加,且直线性 分布。 土质学与土力学 55-3 吉林大学建设工程学院
土质学与土力学 55—3 吉林大学建设工程学院 研究目的:确定土体的初始应力状态 研究方法:土体简化为连续体,应用连续体力学 (例如弹性力学)方法来 研究土中应力的分布。 5.2 土中自重应力 假设天然土体是一个半无限体,地面以下土质均匀,天然重度为 (kN/m3 ),则在天然地面下任意深度z(m)处的竖向自重应力cz (kPa),可 取作用于该深度水平面上任一单位面积上土柱的重量zl计算,即: cz= z cz沿水平面均匀分布,且与z成正比,即随深度增加而增加,且直线性 分布

第5章地基中的应力计算 地基中除有作用于水平面上的竖向自重应力外,在竖直面上还作用有水平 向的侧向自重应力。由于地基中的自重应力状态属于侧限应力状态,故66,, 且o=oy,根据广义虎克定理,侧向自重应力o和og应与oa成正比,而剪应力 均为零,即 Ocx-OCy=KoOcz Lxy=Ty-Tix=0 式中K,一比例系数,称为土的侧压力系数或静止土压力系数。它是侧限条 件下土中水平向有效应力与竖直向有效应力之比。 土质学与土力学 55-4 吉林大学建设工程学院
土质学与土力学 55—4 吉林大学建设工程学院 地基中除有作用于水平面上的竖向自重应力外,在竖直面上还作用有水平 向的侧向自重应力。由于地基中的自重应力状态属于侧限应力状态,故 x= y=0, 且cx=cy,根据广义虎克定理,侧向自重应力cx和cy应与cz成正比,而剪应力 均为零,即 cx = cy = K0cz xy = yz =zx =0 式中 K0―比例系数,称为土的侧压力系数或静止土压力系数。它是侧限条 件下土中水平向有效应力与竖直向有效应力之比
第5章地基中的应力计算 天然地面 於於个然於於杰於於於於於於不 粒间应力是通过土颗 粒接触点传递的,是影响 土体强度的重要因素,故 粒间力在截面上的平均应 力成为有效应力。 Oa=Yz (a) (b) 定义: 土中自重应力为土自身有效 重力在土体内引起的应力 均质土中的应力图 土质学与土力学 55-5 吉林大学建设工程学院
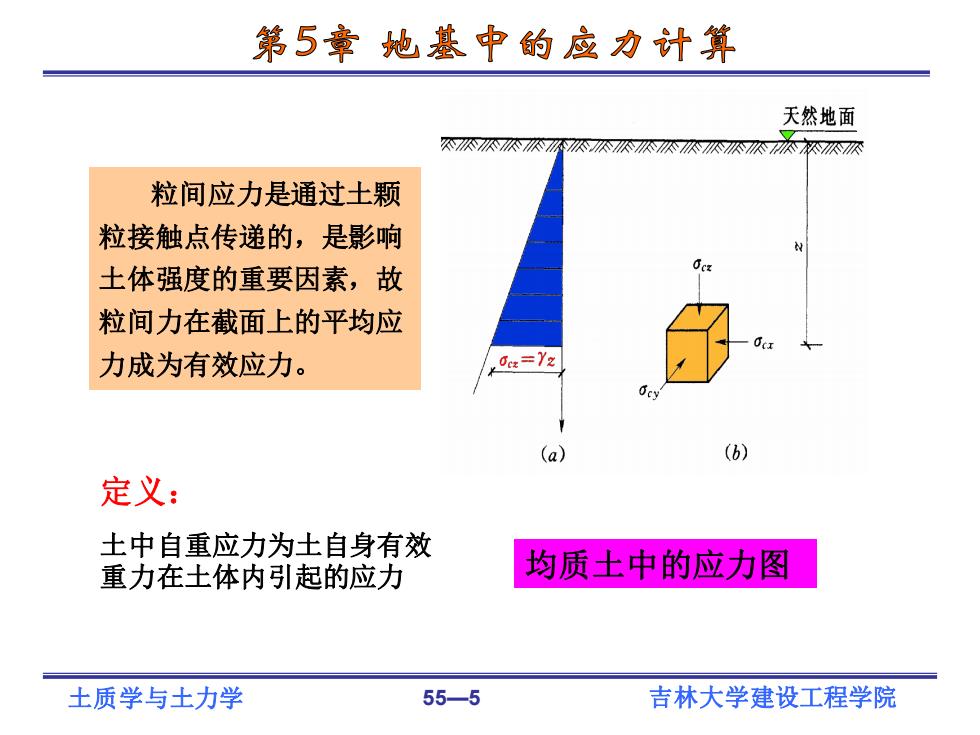
土质学与土力学 55—5 吉林大学建设工程学院 均质土中的应力图 粒间应力是通过土颗 粒接触点传递的,是影响 土体强度的重要因素,故 粒间力在截面上的平均应 力成为有效应力。 定义: 土中自重应力为土自身有效 重力在土体内引起的应力
第5章地基中的应力计算 成层地基土中自重应力 若天然地面下深度z范围内各层土 天然地面 於不 的厚度自上而下分别为h、h2、…hu, Yihi 成层土自重应力为高度z土柱中各层土 重的总和,可得到的计算公式: G线 Yih+rzh2 地下水位 ,为 ∑y,h Yh十Y2h2+yh3 式中 不透水层 σ。一天然地面下任意深度处的竖 y4,4 Yh1+Yh2十Y3h3 77777777777777 77777777 向有效自重应力(kPa); +Y4h4十ye(h3+h) n一深度z范围内的土层总数 h,一第层土的厚度(m); 一第层土的天然重度,对地下 成层土中竖向自重应力沿深 度的分布 水位以下的土层取有效重度?(kN/m3).。 土质学与土力学 55-6 吉林大学建设工程学院
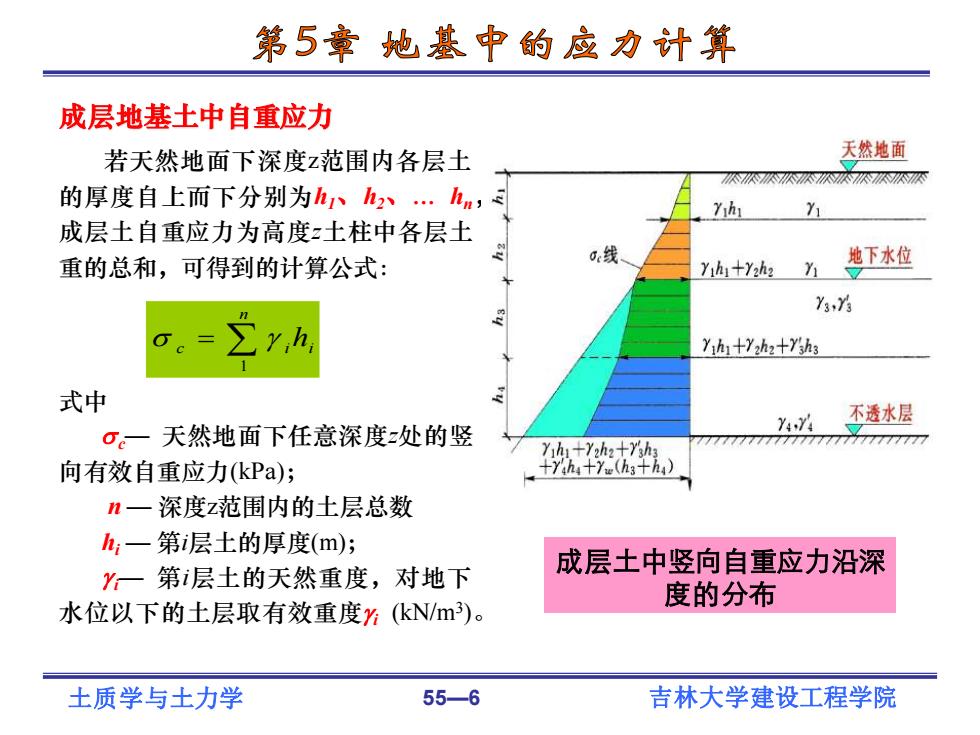
土质学与土力学 55—6 吉林大学建设工程学院 成层土中竖向自重应力沿深 度的分布 成层地基土中自重应力 若天然地面下深度z范围内各层土 的厚度自上而下分别为h1、h2、… hn, 成层土自重应力为高度z土柱中各层土 重的总和,可得到的计算公式: 式中 c— 天然地面下任意深度z处的竖 向有效自重应力(kPa); n — 深度z范围内的土层总数 hi — 第i层土的厚度(m); i— 第i层土的天然重度,对地下 水位以下的土层取有效重度 i (kN/m3 )。 = n c i hi 1

第5章地基中的应力计算 注意 地下水位位于同一土层中,计算自重应力时,地下 水位面应作为分层的界面。 在地下水位以下,如埋藏有不透水层,由于不透水 层中不存在水的浮力,所以层面及层面以下的自重应 力应按上覆土层的水土总重计算。 土质学与土力学 55-7 吉林大学建设工程学院
土质学与土力学 55—7 吉林大学建设工程学院 地下水位位于同一土层中,计算自重应力时,地下 水位面应作为分层的界面。 在地下水位以下,如埋藏有不透水层,由于不透水 层中不存在水的浮力,所以层面及层面以下的自重应 力应按上覆土层的水土总重计算。 注意
第5章她基中的应力计算 dc(kPa) 【例题5一1】 某建筑场地的地质 柱状图和土的有关指标列于图5一3和表 45.5 5一1中。试计算地面下深度为2.5m、 5.0m和9.0m处的自重应力,并绘制自 74.7 109.7 重应力分布图。 92.5 147.5 解:计算过程及结果见下表 之(m) 土的物理指标 总自重 有效 深度 总自重应力 水压力 d, 应力增量 自重应力 (m) 层 (kPa) (kPa) kN/m3 % (kPa) (kPa) .0 0.0 0.0 0.0 0.0 2.5 ① 18.2 2.71 18.34 18.202.5=45.5 45.5 U.0 45.5 6.0 18.343.5=64.2 109.7 3.510.0-35.0 74.7 S.U ② 18.9 2.73 18.9c 35 18.90s2.0=37.8 147.5 5.5x10.0-55.0 92.5 备注 地下水位位于地表下2.5m,水的重度取Y=10.0kN/m 土质学与土力学 55-8 吉林大学建设工程学院
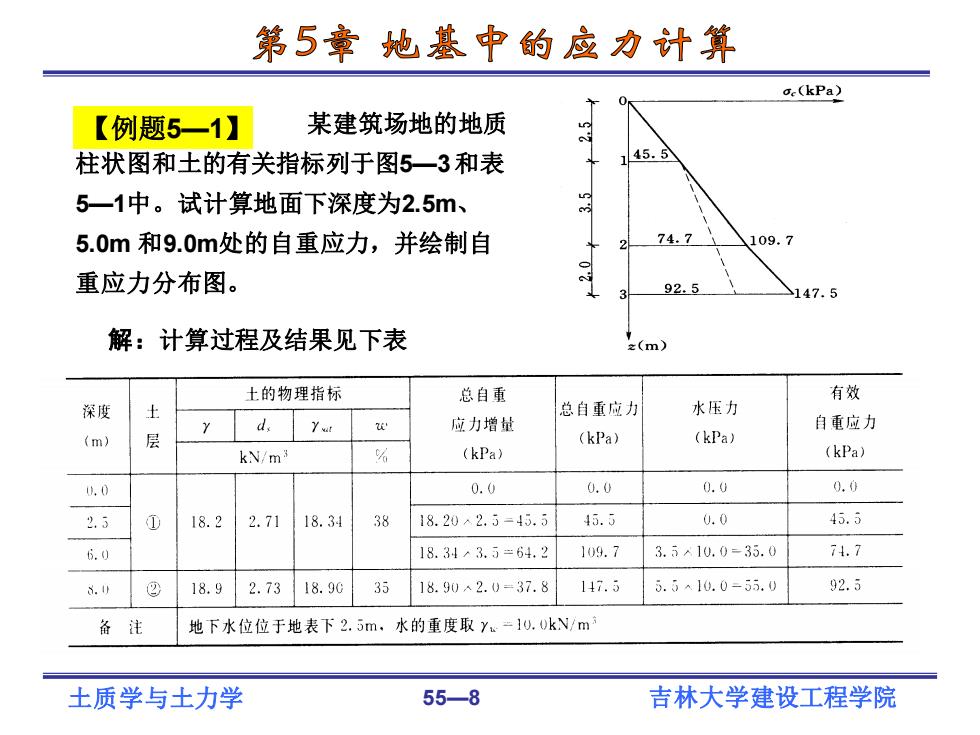
土质学与土力学 55—8 吉林大学建设工程学院 【例题5—1】 某建筑场地的地质 柱状图和土的有关指标列于图5—3 和表 5—1中。试计算地面下深度为2.5m、 5.0m 和9.0m处的自重应力,并绘制自 重应力分布图。 解:计算过程及结果见下表

第5章她基中的应力计算 5.3基底压力和基底附加压力 建筑物着载通过基础传递给地基,基础底面传递给地基 表面的压力,称基底在力。 基底压力的分布规律主要是取决于上部结构、基础的刚度和地基的变形条 件,是三者共同作用的结果。 基础刚度的影响 柔性基础能随着地基土表面而变形,作用在基础底面上的压力分布与作 用在基础上的荷载分布完全一样。因此,若上部荷载均匀分布,基底接触压 力也为均匀分布。 绝对刚性基础的基础底面保持平面,即基础各点的沉降大小一样,基础 底面上的压力分布不同于上部荷载的分布情况。 土质学与土力学 55-9 吉林大学建设工程学院
土质学与土力学 55—9 吉林大学建设工程学院 基底压力的分布规律主要是取决于上部结构、基础的刚度和地基的变形条 件,是三者共同作用的结果。 基础刚度的影响 柔性基础能随着地基土表面而变形,作用在基础底面上的压力分布与作 用在基础上的荷载分布完全一样。因此,若上部荷载均匀分布,基底接触压 力也为均匀分布。 绝对刚性基础的基础底面保持平面,即基础各点的沉降大小一样,基础 底面上的压力分布不同于上部荷载的分布情况。 5.3 基底压力和基底附加压力 建筑物荷载通过基础传递给地基,基础底面传递给地基 表面的压力,称基底压力
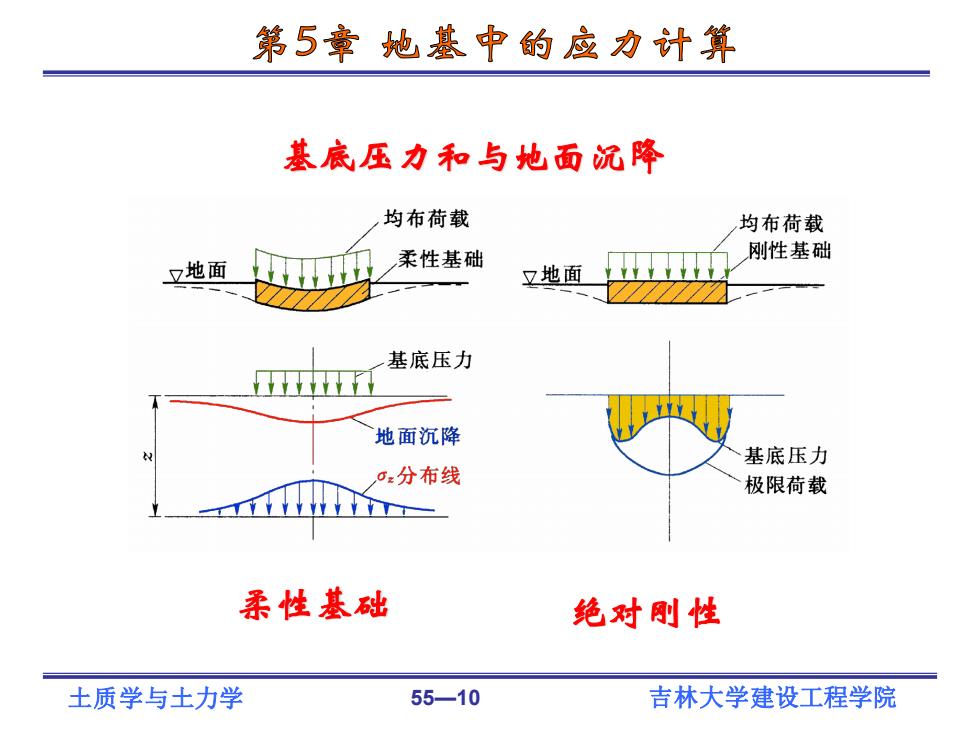
第5章地基中的应力计算 基底压力和与地面沉降 均布荷载 均布荷载 柔性基础 刚性基础 又地面 又地面 基底压力 地面沉降 基底压力 0z分布线 极限荷载 柔性基础 绝对刚性 土质学与土力学 55-10 吉林大学建设工程学院
土质学与土力学 55—10 吉林大学建设工程学院 基底压力和与地面沉降 柔性基础 绝对刚性