
U K 第十章动载荷 本章内容: 1概述 2动静法的应用 3强迫振动的应力计算 4杆件受冲击时的应力和变形 5冲击韧性
1 第十章 动载荷 本章内容: 1 概述 2 动静法的应用 3 强迫振动的应力计算 4 杆件受冲击时的应力和变形 5 冲击韧性

U K §10.1概述 1 动载荷 静载荷 载荷从零开始缓慢地增加到最终值。 可认为构件始终处于平衡状态。 动载荷 随时间明显变化的载荷,即具有较大 加载速率的载荷。 实验表明: 在动载荷作用下,只要应力不超过比例极限, 胡克定律仍成立,且弹性模量与静载时相同。 2动载荷问题分类
2 §10. 1 概述 1 动载荷 静载荷 载荷从零开始缓慢地增加到最终值。 可认为构件始终处于平衡状态。 动载荷 随时间明显变化的载荷,即具有较大 加载速率的载荷。 实验表明: 在动载荷作用下,只要应力不超过比例极限, 胡克定律仍成立,且弹性模量与静载时相同。 2 动载荷问题分类

2动载荷问题分类 1)构件有加速度时的应力计算; 2)冲击问题; 3)振动问题; 4)交变载荷
3 1) 构件有加速度时的应力计算; 2) 冲击问题; 3) 振动问题; 4) 交变载荷。 2 动载荷问题分类

U K §10.2动静法的应用 1动静法 即为理论力学中介绍的达朗伯原理 2匀加速平动构件中的动应力分析 例子 R 设杆以匀加速度a作平动, 截面积为A,比重为y。 加上惯性力系。 9a 分布载荷中,包括自重 和惯性力。则:9=4+a=11+
4 §10. 2 动静法的应用 1 动静法 即为理论力学中介绍的达朗伯原理。 2 匀加速平动构件中的动应力分析 例子 设杆以匀加速度a作平动, 加上惯性力系。 a 截面积为A,比重为。 qd R R l b 分布载荷中,包括自重 和惯性力。 则: qd = a g A + (1 ) g a A = A +

分布载荷中,包括自重 a R 和惯性力。 则: g,=Ay+a=40+ g 加速度为零时 :9st =Ay 加速度为a时: 9a=9s(1+ 记:Ka=1+ a 动荷系数 若忽略自重,则K。= a
5 a qd R R l b 分布载荷中,包括自重 和惯性力。 则: qd = a g A + (1 ) g a A = A + 加速度为零时: q = A st 加速度为a时: (1 ) d st g a q = q + 记: g a Kd =1+ ⎯⎯ 动荷系数 若忽略自重,则 g a Kd =

U K 加速度为a时: 9a=91+4) 记:K=1+ 动荷系数 若忽略自重,则 Ka 对线性系统 内力、应力、应变和变形都与外力成线性关系。 动载荷问题的求解 1)求出动荷系数; 2)按静载荷求解应力、应变、变形等; 3)将所得结果乘以动荷系数K即可
6 加速度为a时: (1 ) d st g a q = q + 记: g a Kd =1+ ⎯⎯ 动荷系数 若忽略自重,则 g a Kd = 对线性系统 内力、应力、应变和变形都与外力成线性关系。 动载荷问题的求解 1) 求出动荷系数; 2) 按静载荷求解应力、应变、变形等; 3) 将所得结果乘以动荷系数 Kd 即可

U K 动载荷问题的求解 1)求出动荷系数; 2)按静载荷求解应力、应变、变形等; 3)将所得结果乘以动荷系数K,即可。 例如: 按静载求出某点的应力为 Ost 则动载下该点的应力为 按静载求出某点的挠度为 则动载下该点的挠度为 Va KaYs 强度条件 oa=K0st≤[o]
7 动载荷问题的求解 1) 求出动荷系数; 2) 按静载荷求解应力、应变、变形等; 3) 将所得结果乘以动荷系数 Kd即可。 例如: 按静载求出某点的应力为 st d = Kd st 则动载下该点的应力为 按静载求出某点的挠度为 st v d d st 则动载下该点的挠度为 v = K v 强度条件 d = Kd st [ ]
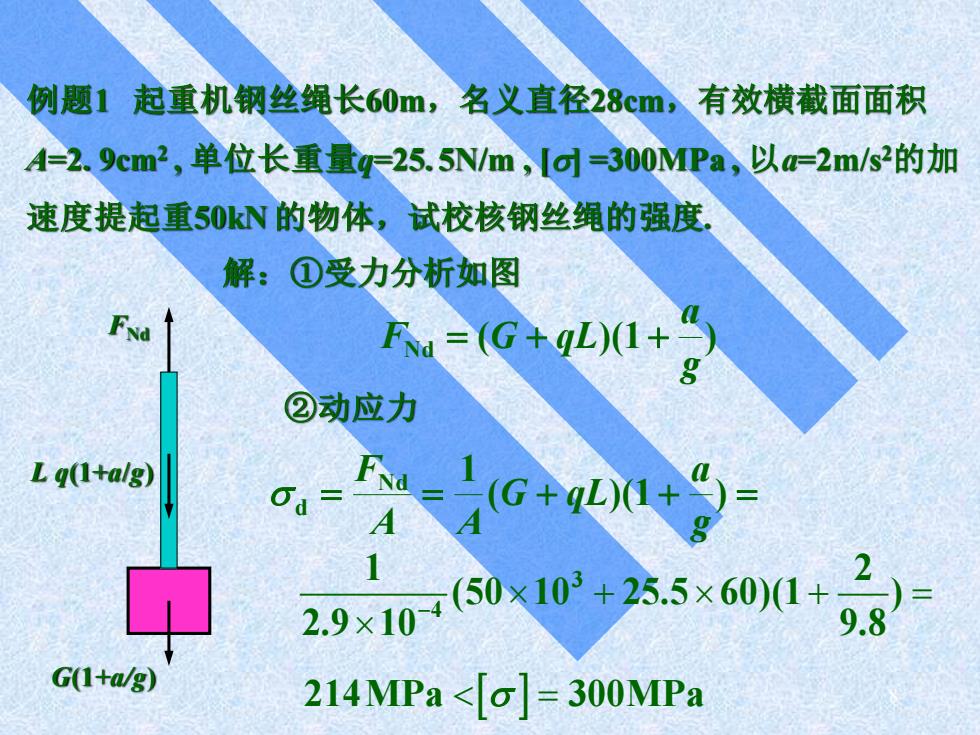
例题1起重机钢丝绳长60m,名义直径28cm,有效横截面面积 A合2.9cm2,单位长重量F25.5N/m,lg-300MPa,以=2m/s2的加 速度提起重50kN的物体,试校核钢丝绳的强度 解:①受力分析如图 FNd=(G+qL)(1+) ②动应力 L g(1+alg) - 29×10(6010+25.5×60)1+ 9.8 G(1+a/g) 214MPa<[o]=300MPa
8 例题1 起重机钢丝绳长60m,名义直径28cm,有效横截面面积 A=2. 9cm2 , 单位长重量q=25. 5N/m , [] =300MPa , 以a=2m/s2的加 速度提起重50kN 的物体,试校核钢丝绳的强度. G(1+a/g) FNd L q(1+a/g) 解:①受力分析如图 ②动应力 3 4 1 2 (50 10 25.5 60)(1 ) 2.9 10 9.8 − + + = 214MPa 300MPa = ( )( ) Nd g a F = G + qL 1 + = = ( + )( + ) = N d d g a G qL A A F 1 1

3匀角速度转动构件中的动应力分析 设圆环以均角速度转动, 厚度t远小于直径D, 截面积为A,比重为y。 加上惯性力系。 an Ro2= Ay D 9a= an= ITTD g 28
9 3 匀角速度转动构件中的动应力分析 设圆环以均角速度转动, 加上惯性力系。 厚度 t 远小于直径D, 截面积为A,比重为。 ω qd 2 an = R 2 2 D = d n a g A q = 2 2 g A D =

9d n=Ro2=2 I → AYa、2g AY D 8 取半圆,求内力 Na 由以前的结论,有: 2V=9D一N。92 Ay D2 2 4g 动应力 Ns_rD'o'rv2 A 4g 8 10
10 2 an = R 2 2 D = d n a g A q = 2 2 g A D = ω qd 取半圆,求内力 Nd Nd 由以前的结论,有: 2Nd = 2 d d q D N = 2 2 4 g A D = 动应力 A Nd d = g D 4 2 2 = g v 2 = qd D