
附录 附录A 平面图形的几何性质 §A-1静矩和形心 §A-2惯性矩和惯性积 §A-3平移轴公式 §A-4转轴公式(了解) §A-5主惯性轴、主惯性矩、形心主惯性矩 2
2 §A-1 静矩和形心 §A-2 惯性矩和惯性积 §A-3 平移轴公式 §A-4 转轴公式(了解) 附录A 平面图形的几何性质 附 录 §A-5 主惯性轴、主惯性矩、形心主惯性矩

§A-1 静矩和形心 一、简单图形的静矩(面积矩) 1、定义: S。=∫4ydA S,=∫zdA 2、量纲:[长度]3;单位:m3、cm3、mm3。 3、静矩的值可以是正值、负值、或零。 3
3 §A-1 静矩和形心 一、简单图形的静矩(面积矩) 1、定义: = = A y A z S zdA S ydA y z dA y z o 2、量纲:[长度]3;单位:m 3 、cm3 、mm3 。 3、静矩的值可以是正值、负值、或零
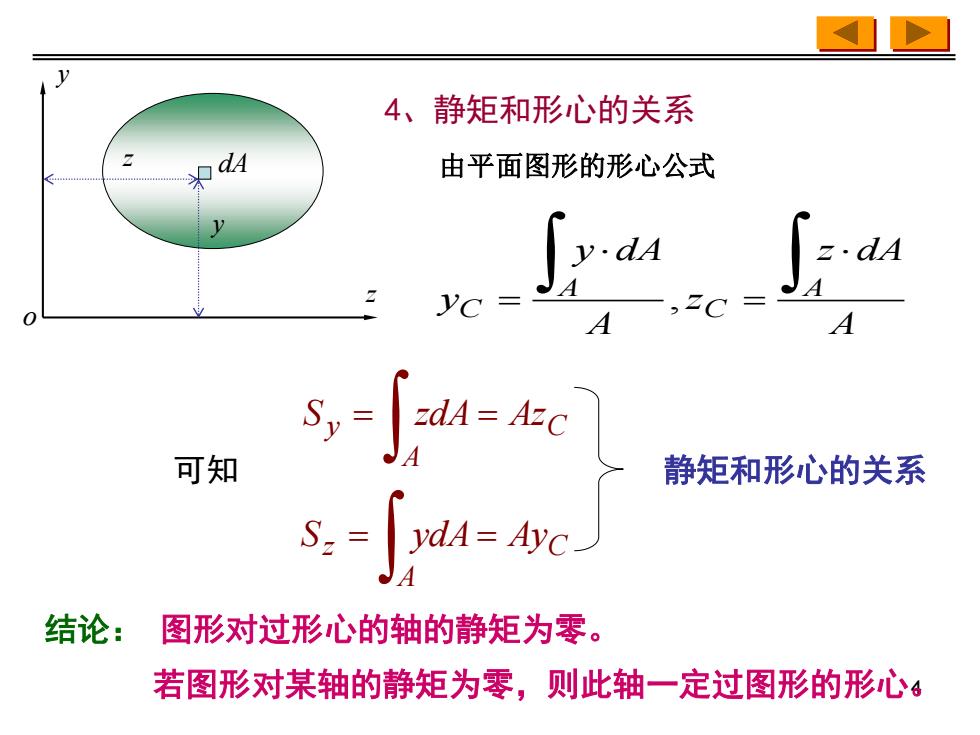
4、静矩和形心的关系 dA 由平面图形的形心公式 =.dA 0 A 可知 静矩和形心的关系 结论: 图形对过形心的轴的静矩为零。 若图形对某轴的静矩为零,则此轴一定过图形的形心4
4 y z dA y z o 4、静矩和形心的关系 可知 A z dA z A y dA y A C A C = = , C A Sy = zdA = Az C A Sz = ydA = Ay 静矩和形心的关系 由平面图形的形心公式 结论: 图形对过形心的轴的静矩为零。 若图形对某轴的静矩为零,则此轴一定过图形的形心

求图形对y,z轴的静矩 及-- a+ =bh(a+)=A 81=t bh 2 10 2 S.ydd =0 2 h 5
5 z y = A z S ydA ZC + = a h a ybdy a h a by + = 2 2 ) 2 ( h = bh a + = AyC b h a dy y z dz = A y S zdA = b zhdz 0 b hz 0 2 2 = 2 b = bh = AzC = A z S ydA c − = 2 2 h h ybdy 2 2 2 2 h h by − = = 0 求图形对y、z 轴的静矩

二、简单图形的形心 yc= 1、形心坐标公式: A A zdA A A A 2、形心确定的规律: (1)图形有对称轴时,形心必在此对称轴上。 (2)图形有两个对称轴时,形心必在此两对称轴的交点处。 6
6 二、简单图形的形心 1、形心坐标公式: A ydA A S y z A c = = A zdA A S z y A c = = 2、形心确定的规律: (1)图形有对称轴时,形心必在此对称轴上。 (2)图形有两个对称轴时,形心必在此两对称轴的交点处

三、组合图形(由若干个基本图形组合而成的图形)的静矩: 基本图形指面积、形心位置已知的图形 S=∑S=∑4ya S,=∑S,m=∑A2a 四、组合图形的形心: ∑S Aiyci = 利用基本图 A A 形的结果,可使 AiZci 组合图形的形心 计算简单 2e= ∑A A 7
7 三、组合图形(由若干个基本图形组合而成的图形)的静矩: z zi i ci S =S =A y y yi i ci S =S =A z 四、组合图形的形心: = i zi c A S y = i yi c A S z A A y i ci = A A z i ci = 利用基本图 形的结果,可使 组合图形的形心 计算简单 基本图形----指面积、形心位置已知的图形

例试确定下图的形心。 解法1:1)、建立坐标如图示,分割图形 A=700mm2,z=45mm,ya =5mm A,=1200mm2,zc2=5mm,y.2=60mm 2)、求形心 ∑A2a-4a+4e2 2e= A A1+A2 C2 120 45×700+5×1200 C(19.7;39.7) ● 1 700+1200 =19.7(mm) ∑A,y-Aya+4,y2 不 80 A A,+A2 5×700+60×1200 700+1200 =39.7(mm) 8
8 1 2 1 1 2 2 A A A z A z A A z z i ci c c c + + = = 例 试确定下图的形心。 1 2 1 1 2 2 A A A y A y A A y y i ci c c c + + = = 80 10 c(19.7;39.7) z y C1 C2 解法1:1)、建立坐标如图示,分割图形 A 700mm , zc1 45mm, yc1 5mm 2 1 = = = A 1200mm , zc2 5mm, yc2 60mm 2 2 = = = 120 700 1200 45 700 5 1200 + + = 2)、求形心 =19.7 ) (mm 39.7( ) 700 1200 5 700 60 1200 = m m + + =

解法二:)、分割图形及建立坐标系,如图所示 A=800mm2,2a=0,y.=0. A2=1100mm2,2e2=-35mm,y.2=60mm 2)、求形心 :气∑4-4+42 A A1+A2 8 -35×1100 =-20.3(mm) 20.3;B4.7) 10×110+80×10 ∑4a=4ya+4y2 80 A A1+A2 60×1100 =34.7(mm) 10×110+80×10 9
9 80 10 20.3( ) 10 110 80 10 35 1100 = − mm + − = c(-20.3;34.7) 解法二:1)、分割图形及建立坐标系,如图所示 z y C2 C1 800 , 0, 0. 1 1 2 A1 = mm zc = yc = A 1100m m , zc2 35m m, yc2 60m m 2 2 = = − = 2)、求形心 34.7( ) 10 110 80 10 60 1100 = mm + = 1 2 1 1 2 2 A A A z A z A A z z i ci c c c + + = = 1 2 1 1 2 2 A A A y A y A A y y i ci c c c + + = =

解法三:负面积法 A,=9600mm2,2c1=40mm,y。1=60mm 10 A2=-70×110mm2,2c2=45mm,y.2=65mm 求形心: 7 2c= >Azaha+Aio A 80 A1+A2 40×96+45×(-77)=19.7(mm) 12×8-7×11 。s ∑4y。=Ay+4,y2 A A1+A2 60×96+65×(-77 2=39.7(mm) 96-77 10
10 解法三:负面积法 19.7( ) 12 8 7 11 40 96 45 ( 77) = m m − + − = z y A 9600mm , zc1 40mm, yc1 60mm 2 1 = = = A 70 110m m , zc2 45m m, yc2 65m m 2 2 = − = = C2 求形心: 39.7( ) 96 77 60 96 65 ( 77) = m m − + − 1 = C C0 1 2 1 1 2 2 A A A z A z A A z z i ci c c c + + = = 1 2 1 1 2 2 A A A y A y A A y y i ci c c c + + = = 80 10 10 z y

§A-2 惯性矩和惯性积 一、简单图形的惯性矩 1、定义: Z >dA dA对z轴的惯性距: dl.y'dA dA对y轴的惯性距: dl.z'dA 图形对z轴的惯性矩:1,=∫ydA, p2=z2+y2 图形对y轴的惯性矩:1,=z'd4 2、量纲:m4、mm4。 A 3、惯性矩是对轴而言(轴惯性矩)。 4、惯性矩的取值恒为正值。 5、极惯性矩:(对o点而言) 1。=p2dM=1。 11
11 §A-2 惯性矩和惯性积 一、简单图形的惯性矩 1、定义: dA对z轴的惯性距: dA对y轴的惯性距: 2、量纲:m 4 、mm4 。 y z dA z y o , 2 = A Iz y dA = A I y z dA 2 dI z y dA 2 = dI y z dA 2 = 3、惯性矩是对轴而言(轴惯性矩)。 4、惯性矩的取值恒为正值。 5、极惯性矩:(对o点而言) = A I o dA 2 p = I 2 2 2 = z + y 图形对z轴的惯性矩: 图形对y轴的惯性矩: