
第七章点的合成运动(复合运动) (11) (例:雨点{对行人:/ 对地: 研究内容:研究同一点的运动在不同参考系中所描述的差别与联系。 §7-1相对运动,牵连运动,绝对运动 y小车 相对地面:旋轮线运动 轮上点M M 一直线行驶 、相对小车:圆周运动 小车相对地面:直线平动 分解「随小车运动 分解 点M相对地面的运动 合成(相对小车运动 《即:复杂运动合成 简单运动) {至于 绝对运动:动点相对于定系的运动 ☆了相对运动:动点相对于动系的运动 点的运动 (牵连运动:动系相对于定系的运动→刚体运动 绝:旋轮线运动 点的运动 要点:站在何处看物体的运动。例:上例 相:圆周运动 牵:小车平动》刚体运动 绝对轨迹 相对轨迹 牵连运动 牵连速度:可。 绝对运动 绝对速度可。 相对运动 相对速度可, 牵连加速度:a。 绝对加速度a。 相对加速度a, 注:牵连速度。、幸连加速度ā。:动系上与动点相重合一点的速度、加速度 “牵连点”(直接对动点影响的一点) y 已知:刀尖M沿x轴运动,x=bsinon(w=常量) 求:刀尖M在旋转工件上切出的痕迹(即:求相对轨迹) (选刀尖M为动点,将动系x'y'与旋转工件固连→分析三种运动) [x'=xcos@t x'=bsin ot cos ot =sin 2ot 动系x'oy':M y'=-xsinot 相对运动方程 y=-bsin2of--(1-cos2or) 旋转工件端面 由相对运动方程酒去时间,得相对轨造方程(?+心+今-公 →圆 4
1 由相对运动方程消去时间 t,得相对轨迹方程: 4 ) 2 ( ) ( 2 2 b 2 b x y 圆 点的运动 要点:站在何处看物体的运动。例:上例 牵连运动 点的运动 动系 x oy : y x t x x t M sin cos : (1 cos 2 ) 2 sin sin 2 2 sin cos 2 t b y b t t b x b t t 相对运动方程 第七章 点的合成运动(复合运动) 研究内容:研究同一点的运动在不同参考系中所描述的差别与联系。 (例:雨点 ) §7-1 相对运动,牵连运动,绝对运动 相对地面:旋轮线运动 →直线行驶 相对小车:圆周运动 小车相对地面:直线平动 点 M 相对地面的运动 (即:复杂运动 简单运动) 定(参考)系:固连于地球上的坐标系(静系) 动(参考)系:固连于相对地球运动物体上的坐标系。 绝对运动:动点相对于定系的运动 相对运动:动点相对于动系的运动 牵连运动:动系相对于定系的运动 刚体运动 绝:旋轮线运动 相:圆周运动 牵:小车平动 刚体运动 绝对轨迹 相对轨迹 牵连速度: e 绝对运动 绝对速度 a 相对运动 相对速度 r 牵连加速度: e a 绝对加速度 a a 相对加速度 r a 注:牵连速度 e 、牵连加速度 e a :动系上与动点相重合一点的速度、加速度, 已知:刀尖 M 沿 x 轴运动, x bsint (ω =常量) 求:刀尖 M 在旋转工件上切出的痕迹(即:求相对轨迹) (选刀尖 M 为动点,将动系 x oy 与旋转工件固连 分析三种运动) 小车 轮上点 M 分解 随小车运动 合成 相对小车运动 参考系 ☆ (11) 对地 :↓ 对行人:↙ “牵连点”(直接对动点影响的一点) 分解 合成 例: ω 旋转工件端面

§7-2点的速度合成定理 绝对位移:MM 相对位移:M,M MM' 牵连位移:MM 有典哥典恶+ t+△t 绝对速度可。牵连速度可。相对速度万, 即:D。=D。+可,速度合成定理(平面矢量方翘 时间:t 般公式。即:适应于牵连运动作任何运动的情况。 平面矢量图 “速度平行四边形”(速度图) i。B 已知:A之w=常量,OA=r,OO1=1 ,求:图示位置时(OA1OO)OB之(或:求O,B杆上B点速度) 0 解:步骤 1、选 动点:OA上A点(即:曲柄端点A:或:滑块A) )1动系:O,B(可不画出动系)(定系一般不需说明) 0 (昌分析该类型选择动点、动系时的要血》 「①动点、动系不要选在同一物体上 注:动点,动系选择基本要点: 【②动点、动系的选择应使相对轨迹清楚明了 2、运动分析一速度图(注意D。=D。+万,的合成关系) V. p才 3、应用合成定理求解 (平面矢量方程,可求解两个未知量) va=r@v r2 U。=Ua·sinp=r0 P+rP+示 r20 例: 已知:w:求:图示时B相D4B(说明B杆平移) 「动点、B上A点 解:选 (一分析该类型选择动点、动系时的要点) 动系:轮0 U.=0A0 0(常量)》 Le 又AB平动,六v4B=DA=e0
2 平面矢量图 φ ω ω 例: 有: t M M t MM t MM t t t 1 0 1 0 0 lim lim lim 注:动点,动系选择基本要点: ①动点、动系不要选在同一物体上 ②动点、动系的选择应使相对轨迹清楚明了 a r 2 2 2 2 2 sin r +l r r +l r r e a 2 2 2 1 1 1 1 r +l r O A O A e e (进而可求得 B ) e OA e OA e a e ctg OA ( 分析该类型选择动点、动系时的要点) §7-2 点的速度合成定理 绝对位移: MM 相对位移: M M 1 牵连位移: MM1 绝对速度 a 牵连速度 e 相对速度 r 即: a e r 速度合成定理(平面矢量方程) 一般公式。即:适应于牵连运动作任何运动的情况。 “速度平行四边形”(速度图) 已知:OA 之ω =常量, OA r OO l 1 , 求:图示位置时( OA OO1 ) O1B 之 1 (或:求 O1B 杆上 B 点速度) 解:步骤: 1、选 ( 分析该类型选择动点、动系时的要点) 2、运动分析→速度图(注意 a e r 的合成关系) 3、应用合成定理求解 v? r v? e vv a (平面矢量方程,可求解两个未知量) 已知:ω ;求:图示时 AB 杆 AB (说明 AB 杆平移) 动点、AB 上 A 点 动系:轮 O 又 AB 平动,∴ AB A e 时间: +Δ φ ω(常量) 例: θ 解: 选 动点:OA 上 A 点(即:曲柄端点 A;或:滑块 A) 动系: O1B (可不画出动系)(定系一般不需说明) ? e r ? a
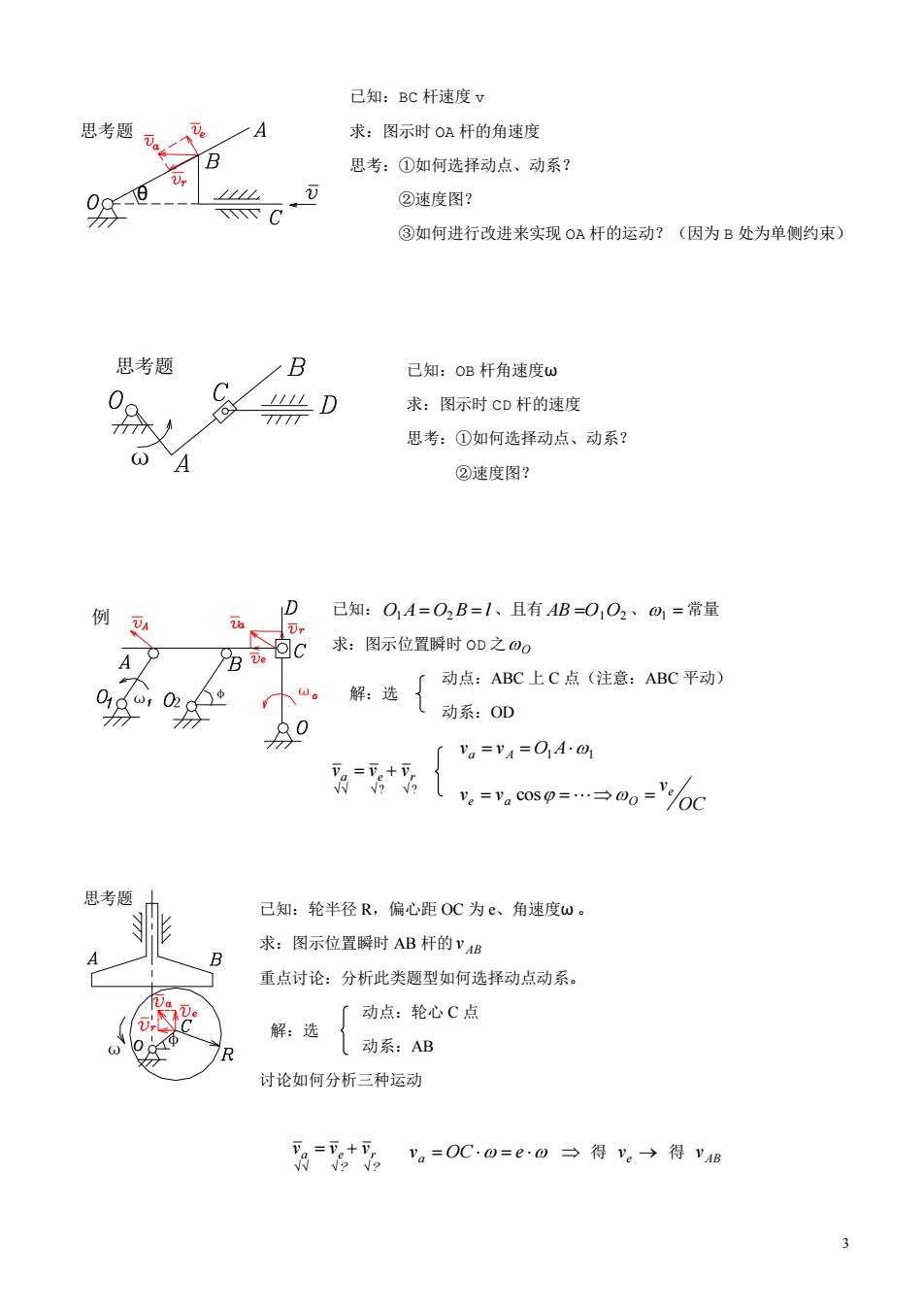
己知:BC杆速度v 思考题一A 求:图示时OA杆的角速度 思考:①如何选择动点、动系 ②速度图? C ③如何进行改进来实现OA杆的运动?(因为B处为单侧约束) 思考题 B 已知:OB杆角速度w C D 7777 求:图示时cD杆的速度 思考:①如何选择动点、动系? A ②速度图? 例4 已知:OA=O2B=1、且有AB-01O2、m=常量 求:图示位置瞬时oD之OO g 。 解:选动点:ABC上C点(注意:ABC平动) 动系:OD 「=v4=OAm 思考题 己知:轮半径R,偏心距OC为、角速度w。 求:图示位置瞬时AB杆的YB 重点讨论:分析此类题型如何选择动点动系。 R 总(c 讨论如何分析三种运动 员=。=0C0=e0得→得v
3 解:选 已知:BC 杆速度 v 求:图示时 OA 杆的角速度 思考:①如何选择动点、动系? ②速度图? ③如何进行改进来实现 OA 杆的运动?(因为 B 处为单侧约束) 已知:OB 杆角速度ω 求:图示时 CD 杆的速度 思考:①如何选择动点、动系? ②速度图? 已知: O A O B l 1 2 、且有 AB O1O2 、1 常量 求:图示位置瞬时 OD 之 O 动点:ABC 上 C 点(注意:ABC 平动) 动系:OD 1 1 v v O A a A OC v v v e e a cos O 已知:轮半径 R,偏心距 OC 为 e、角速度ω 。 求:图示位置瞬时 AB 杆的 AB v 重点讨论:分析此类题型如何选择动点动系。 动点:轮心 C 点 动系:AB 讨论如何分析三种运动 va OC e 得 ve 得 AB v θ 思考题 ω 思考题 ω φ ω 2 例 ? ? a e r v v v φ ω 思考题 解:选 ? r ? a e v v v
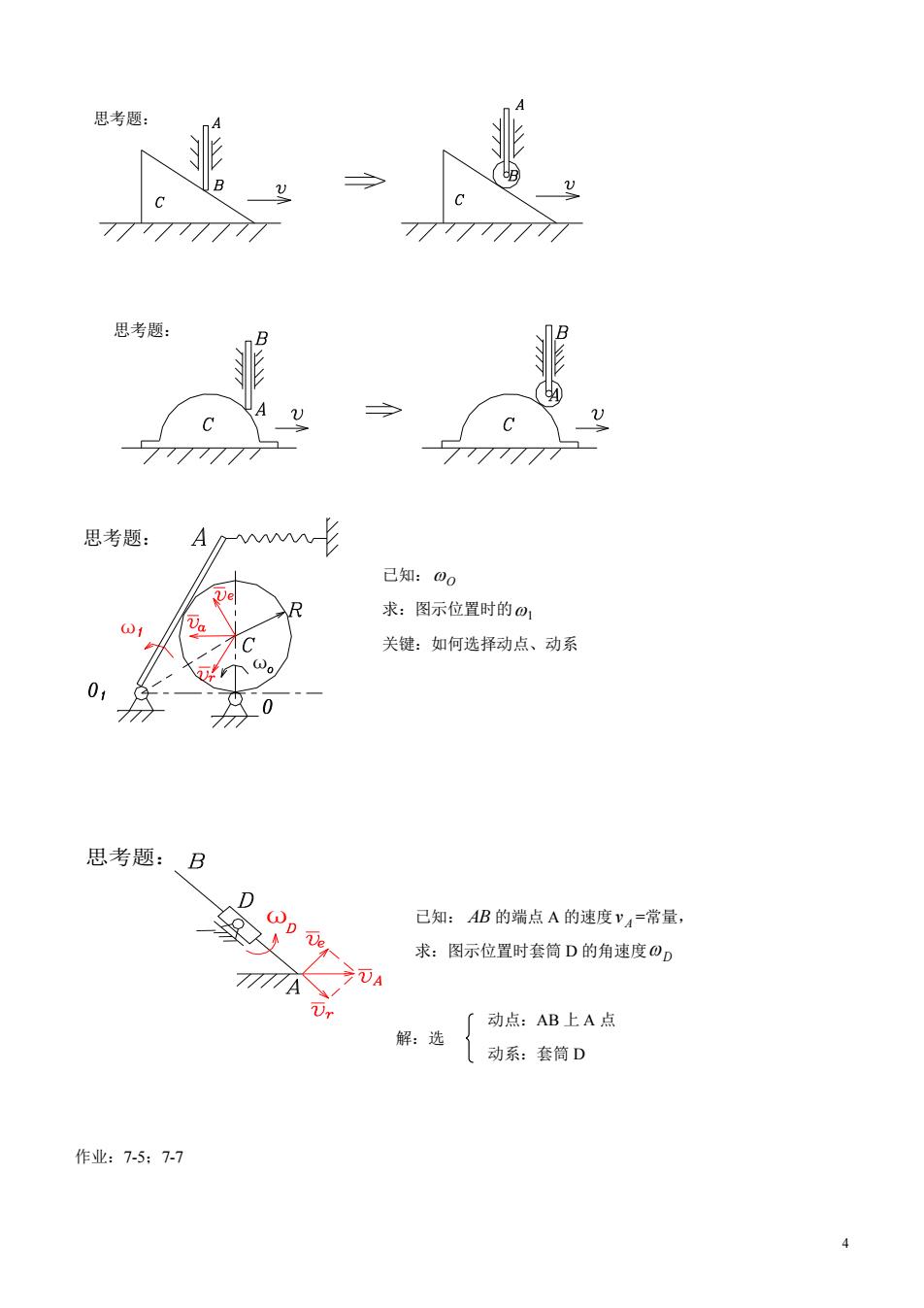
思考题 思考题 思考题 A影 己知:0o 求:图示位置时的 关键:如何选择动点、动系 01 思考题:、B D 己知:AB的端点A的速度=常量 求:图示位置时套筒D的角速度) 7777A A 「动点:AB上A点 解:选 (动系:套简D 作业:7-5:7-7 4
4 ω 思考题: 已知: O 求:图示位置时的 1 关键:如何选择动点、动系 已知: AB 的端点 A 的速度 A v =常量, 求:图示位置时套筒 D 的角速度 D 动点:AB 上 A 点 动系:套筒 D 作业:7-5;7-7 思考题: 思考题: ω 思考题: ω 解:选