
复习 掌握内容 1.变形固体的基本假设 连续性 均匀性 各向同性 小变形 2.应力、应变的基本概念 求内力的基本方法(截,代,求) 3.杆件变形的基本形式 轴向拉压,剪切,扭转,弯曲
1.变形固体的基本假设 连续性 均匀性 各向同性 小变形 掌握内容 2. 应力、应变的基本概念 求内力的基本方法(截,代,求) 3. 杆件变形的基本形式 轴向拉压, 剪切, 扭转, 弯曲

复习 §1-1材料力学的任务及研究对像 The tasks and research objects of mechanics of materials 一、任务(task) 材料力学是研究构件承载能力的一门学科。 强度(strength) 承载能力 (carrying 刚度(stiffness) capacity 稳定性(stability)
§1-1 材料力学的任务及研究对象 The tasks and research objects of mechanics of materials 一、任务 (task) 材料力学是研究构件承载能力的一门学科。 承载能力 (carrying capacity ) 强度(strength) 刚度(stiffness) 稳定性(stability)

义习 51-2变形固体的基本假设 (The basic assumptions of deformable body 一、 连续性假设(continuit女y assumption) 物质密实地充满物体所在空间,毫无空隙。 二、均匀性假设(homogenization assumption) 物体内,各处的力学性质完全相同
§1-2 变形固体的基本假设 (The basic assumptions of deformable body ) 一、连续性假设 (continuity assumption) 物质密实地充满物体所在空间,毫无空隙。 二、均匀性假设(homogenization assumption) 物体内,各处的力学性质完全相同

复习 三、各向同性假设(isotropy assumption) 组成物体的材料沿各方向的力学性质完全相同。 四、小变形假设(neglecting deformation assumption) 材料力学所研究的构件在载荷作用下的变形与原始尺寸 相比甚小,故对构件进行受力分析时可忽略其变形。 课间休息
三、各向同性假设(isotropy assumption) 组成物体的材料沿各方向的力学性质完全相同。 四、小变形假设(neglecting deformation assumption) 材料力学所研究的构件在载荷作用下的变形与原始尺寸 相比甚小,故对构件进行受力分析时可忽略其变形。 课间休息

轴向粒压 剪切 狃转 弯曲 受力 m m 变形特点 1=9549- P(kw) a2mmm) 内力 轴力N 剪力Q 扭矩T 剪2=∑P 截面法) N=∑P 挤压力P T=∑m 弯矩1= ∑Px N T 应力 jq A A 12b 强度 T≤ W. 条件 max s ≤ W
轴向拉.压 剪 切 扭 转 弯 曲 受力 变形特点 P P P P P P m m 内力 (截面法) 轴力 N 剪力 Q 挤压力 Pjy 扭矩 T 剪力 弯矩 应力 A N = Ajq Q = jy jy jy A P = P I T = Z I My = I b QS Z Z = 强度 条件 = min max max A N jy jy = WP Tmax max = max max max WZ M N =P一侧 T =m一侧 Q =P一侧 m =Px一侧 ( / min) ( ) 9549 n r P kw m = m

复 轴向拉压 扭转 弯曲 NL T·b 变形 △L= EA G·Ip Ef(x)”=-M 刚度条件 △L 180 L GIp =[o1 t sIf]er slo π 虎克定律 0= Ea GY 超静定 1、静平衡方程 问题 2、变形协调方程
变形 刚度条件 EA NL L= P G I T L = = max 180 GIP T EIf (x) = −M(x) max max f f 轴向拉.压 扭 转 弯 曲 L L = 虎克定律 = E = G 超静定 问题 1、静平衡方程 2、变形协调方程
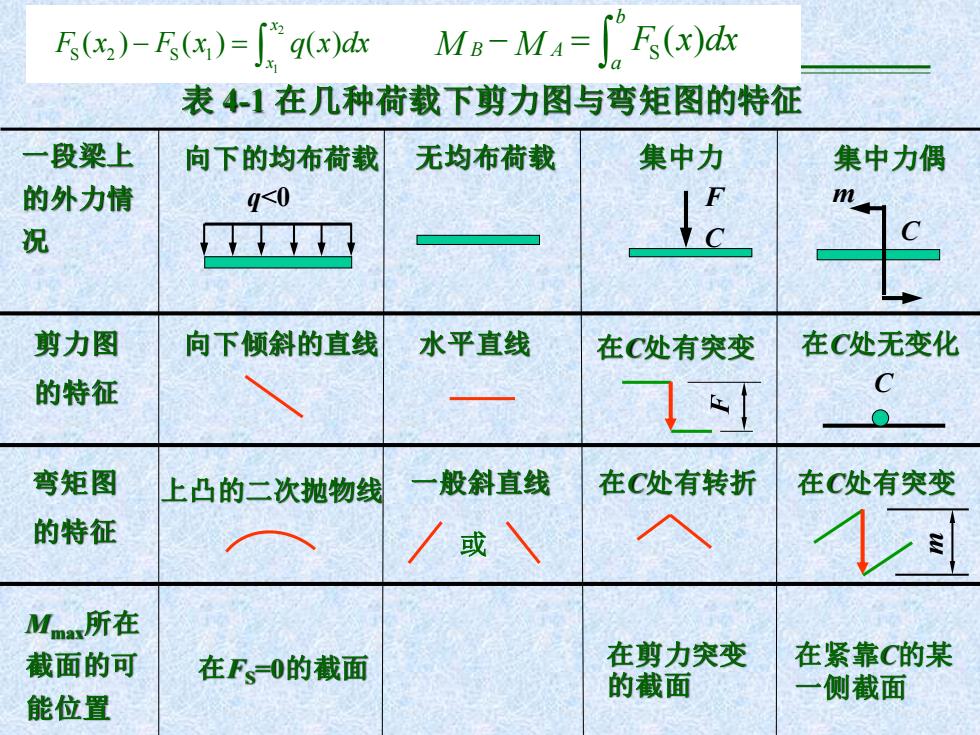
E(3)-E(x)=∫qx)d Ma-M=[F(x)dx 表41在几种荷载下剪力图与弯矩图的特征 一段梁上 向下的均布荷载 无均布荷载 集中力 集中力偶 的外力情 4<0 况 剪力图 向下倾斜的直线 水平直线 在C处有突变 在C处无变化 的特征 弯矩图 上凸的二次抛物线 一般斜直线 在C处有转折 在C处有突变 的特征 /或、 Mmas所在 截面的可 在F、O的截面 在剪力突变 在紧靠C的某 的截面 一侧截面 能位置
无均布荷载 集中力 F C 集中力偶 m C 向下倾斜的直线 上凸的二次抛物线 在FS=0的截面 水平直线 一般斜直线 或 在C处有转折 在剪力突变 的截面 在紧靠C的某 一侧截面 一段梁上 的外力情 况 剪力图 的特征 弯矩图 的特征 Mmax所在 截面的可 能位置 表 4-1 在几种荷载下剪力图与弯矩图的特征 q<0 向下的均布荷载 在C处有突变 在C处有突变 m 在C处无变化 C S ( ) b B A a M M− = F x dx 2 1 S 2 S 1 ( ) ( ) ( ) x x F x F x q x dx − =
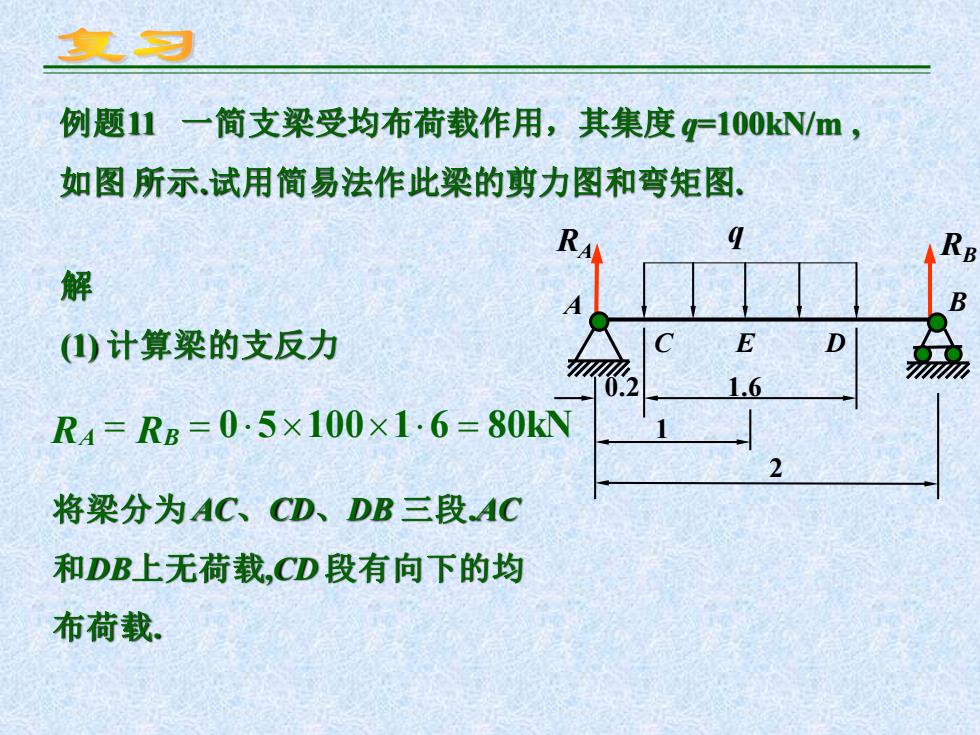
复习 例题11 一简支梁受均布荷载作用,其集度g一100kN/m, 如图所示试用简易法作此梁的剪力图和弯矩图. RA 9 解 (①)计算梁的支反力 E 0.2 1.6 R4=RB=0.5×100×1·6=80kN 将梁分为AC、CD、DB三段AC 和DB上无荷载,CD段有向下的均 布荷载
例题11 一简支梁受均布荷载作用,其集度q=100kN/m , 如图 所示.试用简易法作此梁的剪力图和弯矩图. 解 (1) 计算梁的支反力 RA RB E q A B C D 0.2 1.6 1 2 RA = RB = 0510016 = 80kN 将梁分为 AC、CD、DB 三段.AC 和DB上无荷载,CD 段有向下的均 布荷载
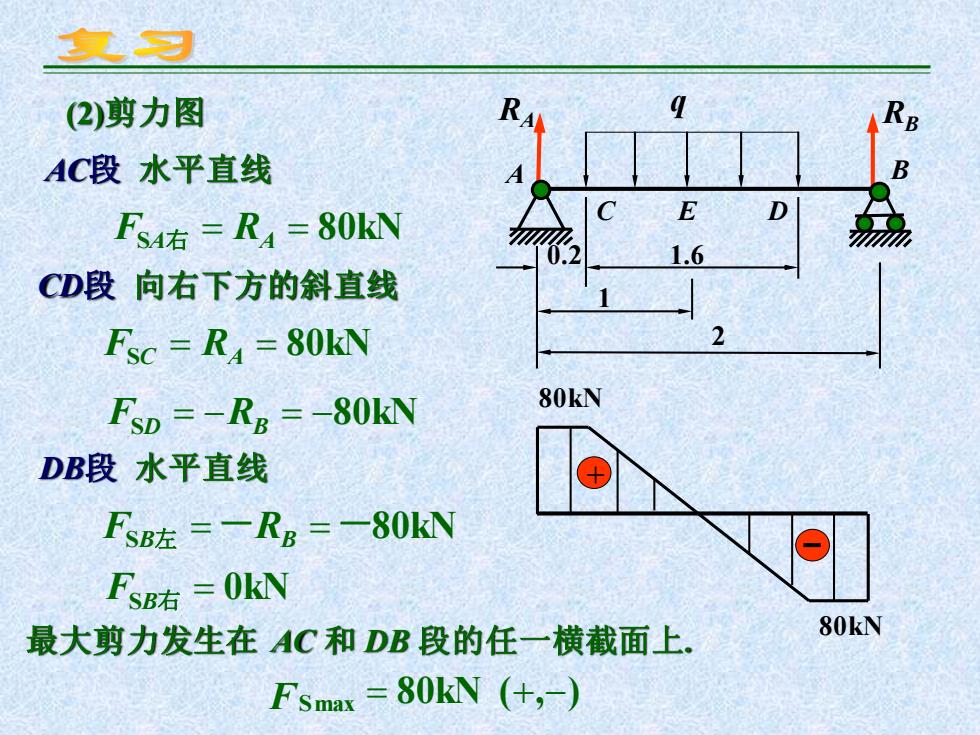
复习 (2)剪力图 AC段水平直线 A F4右=R4=80kN 1.6 CD段向右下方的斜直线 FSC =R4=80kN FSD =-RB =-80kN 80kN DB段水平直线 FsB左=-Rg=一80kN FsB右=0kN 最大剪力发生在AC和DB段的任一横截面上 80kN Fsmax=80kN (+,-
(2)剪力图 + 80kN 80kN AC段 水平直线 FSA右 = RA = 80kN CD段 向右下方的斜直线 FSC = RA = 80kN FSD = −RB = −80kN DB段 水平直线 FSB左 =-RB =-80kN FSB右 = 0kN 最大剪力发生在 AC 和 DB 段的任一横截面上. max 80kN ( , ) FS = + − RA RB E q A B C D 0.2 1.6 1 2
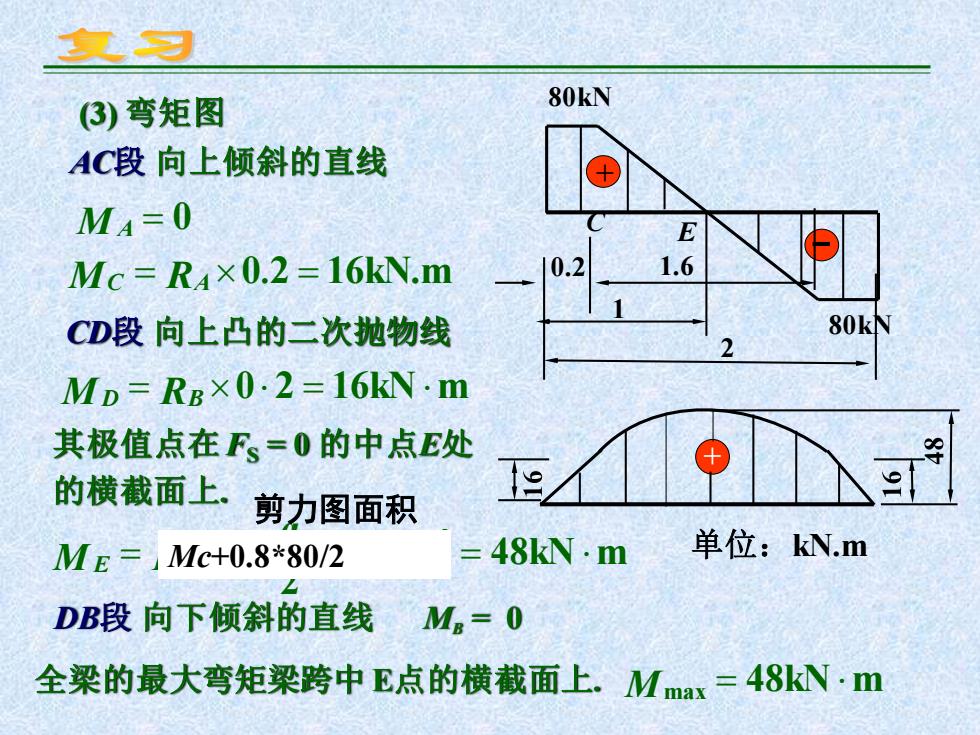
复习 3)弯矩图 80kN AC段向上倾斜的直线 M4=0 Mc=R4×0.2=16kN.m 0.2 1.6 CD段向上凸的二次抛物线 80k MD=Rε×0.2=16kNm 其极值点在F、=0的中点E处 的横截面上 9 剪力图面积 ME=Mc+0.8*80/2 =48kN·m 单位:kN.m DB段向下倾斜的直线 M=0 全梁的最大弯矩梁跨中E点的横截面上.Mmax=48kN,m
(3) 弯矩图 AC段 向上倾斜的直线 CD段 向上凸的二次抛物线 M A = 0 MC = RA 0.2 = 16kN.m MD = RB 0 2 = 16kN m 其极值点在FS = 0 的中点E处 的横截面上. (1 0 2) 48kN m 2 1 2 = − − = q ME RA DB段 向下倾斜的直线 MB = 0 + 单位:kN.m 全梁的最大弯矩梁跨中 E点的横截面上. Mmax = 48kN m Mc+0.8*80/2 + 80kN 80kN C 0.2 1.6 1 2 E 剪力图面积