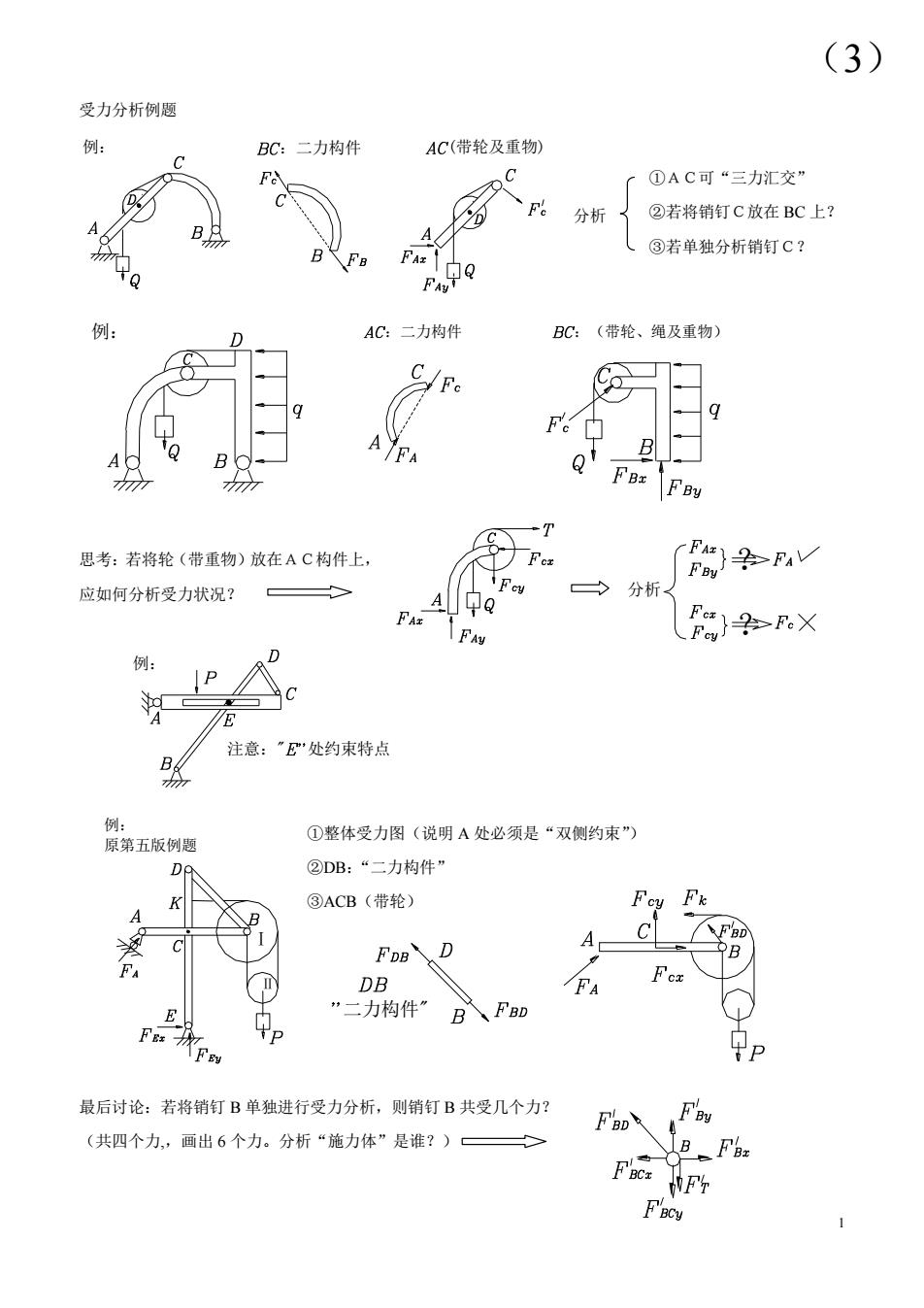
(3) 受力分析例题 BC:二力构件 AC(带轮及重物) Fe C ①AC可“三力汇交” 分析 ②若将销钉C放在BC上? A B (③若单独分析销钉C? AC:二力构件 BC:(带轮、绳及重物) Fe F。中 B Q1- BxFB助 -T 思考:若将轮(带重物)放在AC构件上 应如何分析受力状况? A中Q 之分析 脚M 阳RX 例: D P 注意:“E处约束特点 B 例: 原第五版例题 ①整体受力图(说明A处必须是“双侧约束”) D ②DB:“二力构件 ③ACB(带轮) DB F A ”二力构件” B、FBD 最后讨论:若将销钉B单独进行受力分析,则销钉B共受几个力? F (共四个力,画出6个力。分析“施力体”是谁?)三 B- F%
1 例: :二力构件 (带轮及重物) 例: :二力构件 :(带轮、绳及重物) 例: 注意:" 处约束特点 分析 受力分析例题 ①AC可“三力汇交” ②若将销钉C放在 BC 上? ③若单独分析销钉C? 思考:若将轮(带重物)放在AC构件上, 应如何分析受力状况? ①整体受力图(说明 A 处必须是“双侧约束”) ②DB:“二力构件” ③ACB(带轮) 最后讨论:若将销钉 B 单独进行受力分析,则销钉 B 共受几个力? (共四个力,,画出 6 个力。分析“施力体”是谁?) Ⅱ Ⅰ 例: 原第五版例题 二力构件" (3) ? ? 分析
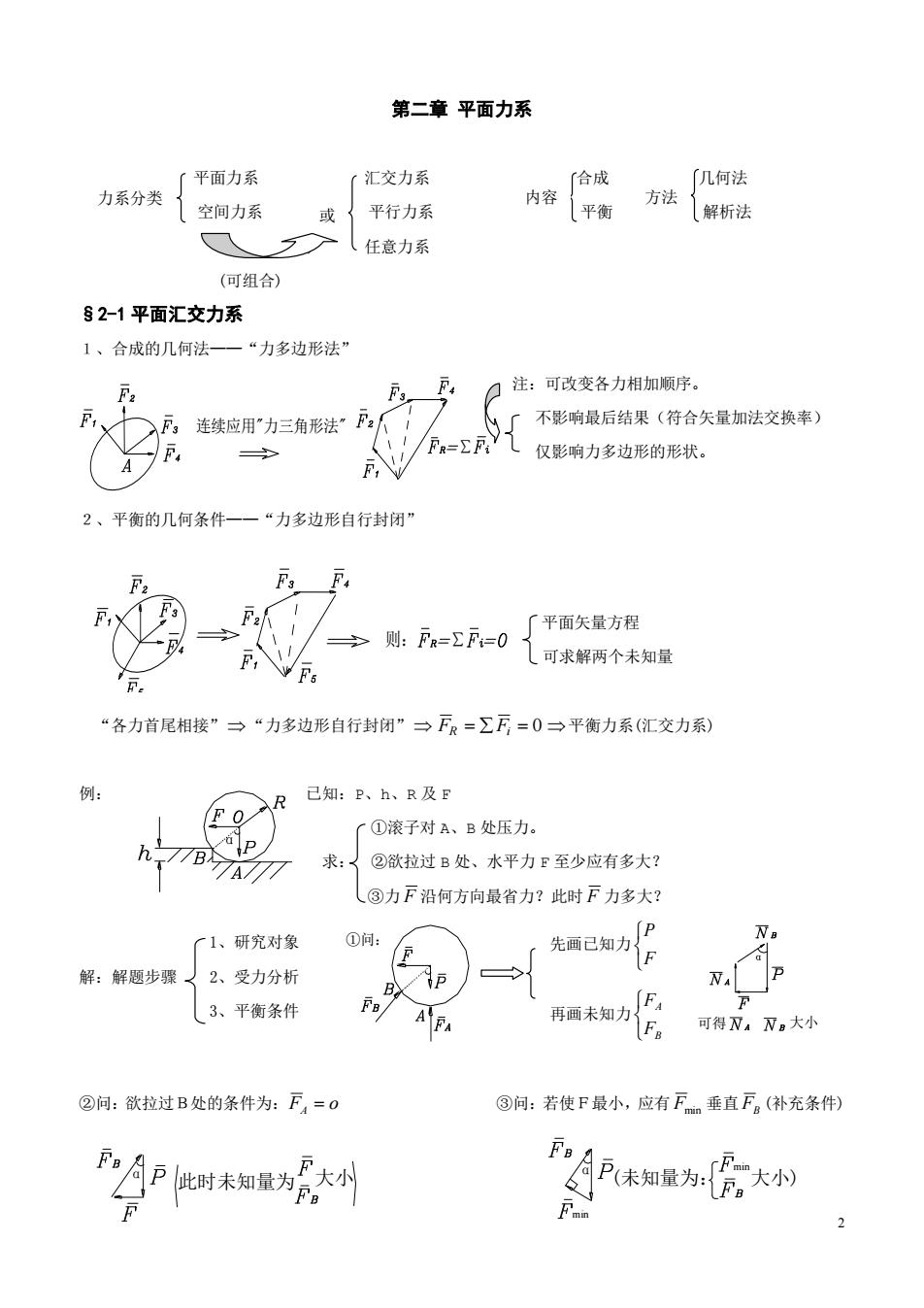
第二章平面力系 {话 「汇交力系 合成 「几何法 或{平行力系 内容平衡 方法 解析法 Q一>(任意力系 (何组合) §2-1平面汇交力系 1、合成的几何法一一“力多边形法 注:可改变各力相加顺序。 F,连续应用“力三角形法”P 不影响最后结果(符合矢量加法交换率】 仅影响力多边形的形状。 2、平衡的几何条件一一“力多边形自行封闭 F. 〔平面矢量方程 则:Fa=F=0 可求解两个未知量 “各力首尾相接”一“力多边形自行封闭”一FR=∑F=0一平衡力系(汇交力系) 例: 己知:P、h、R及E 了①滚子对A、B处压力. 求:{②欲拉过B处、水平力至少应有多大? (③力下沿何方向最省力?此时下力多大? 了1、研究对象 ①向: 先画己知方P 解:解题步骤2、受力分析 3、平衡条件 再画未知力 可得N4N。大小 ②问:欲拉过B处的条件为:F=0 ③问:若使F最小,应有F垂直F(补充条件 F月此时未知量 F大小 AP未知量为:大
2 ①问: 可得 大小 α 先画已知力 F P 再画未知力 B A F F 第二章 平面力系 平面力系 汇交力系 合成 几何法 空间力系 平行力系 平衡 解析法 ) 任意力系 (可组合) §2-1 平面汇交力系 1、合成的几何法——“力多边形法” 注:可改变各力相加顺序。 不影响最后结果(符合矢量加法交换率) 仅影响力多边形的形状。 2、平衡的几何条件——“力多边形自行封闭” 平面矢量方程 可求解两个未知量 “各力首尾相接” “力多边形自行封闭” FR Fi 0 平衡力系(汇交力系) 例: 已知:P、h、R 及 F ①滚子对 A、B 处压力。 求: ②欲拉过 B 处、水平力 F 至少应有多大? ③力 F 沿何方向最省力?此时 F 力多大? 1、研究对象 解:解题步骤 2、受力分析 3、平衡条件 ②问:欲拉过B处的条件为: FA o ③问:若使F最小,应有 Fmin 垂直 FB (补充条件) 连续应用"力三角形法" ∑ 则: ∑ α α 此时未知量为 大小 (未知量为: min大小) α min 力系分类 或 内容 方法

2、合成的解析法 ①先利用合力投影定理,求合力F。的投影: ∫Fx=∑F =∑F (“合力投影等于各分力投影之代数和") ②再利用合力投影F ,求合力F,的方向 「大小 平衡的解析条件一一平衡方程 平衡L安力系房=Σ=0一F=0→E+位可0→位,0 ZF,=0 (注、平面汇交力系有两个独立平衡方程,可求解两个未知量。) 例:求:A、D两处反力 ①研究对象:整体(也可选择AB) 解: ②受力分析(注意二力构件及三力平衡汇交的应用) 【③平衡条件(方程) 3 asp= cosp=而 教可认L三测应手以图示明坐标) ∑F=0 FA COS--Fcos45=0 ∑F,=o一sino+Fo sin45°-Q=0(“注意投影的±号")
3 例: Φ ) 一般可默认: 否则应予以图示说明坐标。) Ry yi Rx xi F F F F 2、合成的解析法 ①先利用合力投影定理,求合力 FR 的投影: (“合力投影等于各分力投影之代数和”) ②再利用合力投影 Ry Rx F F ,求合力 FR 的 方向 大小 平衡的解析条件——平衡方程 平衡(汇交)力系 FR = Fi =0 F R =0 F + F =0 2 y 2 x 0 0 F = F y x (注、平面汇交力系有两个独立平衡方程,可求解两个未知量。) 例:求:A、D 两处反力 ①研究对象:整体(也可选择AB) 解: ②受力分析(注意二力构件及三力平衡汇交的应用) ③平衡条件(方程) F o F o y x sin sin 45 0 cos — cos 0 -F F Q F F 45 = A D A D (“注意投影的 号”) Φ 10 cos 1 10 3 cos

求:平衡时AB、BC两杆的受力(忽略摩擦、绳和杆自重,不计B轮尺寸国) G是否必要?! 60° 解:轮B(忽略大小,视为一点,即:实际是将轮B视为销钉) 7 (注意:AB、BC均为二力构件) B c ∑F=0-FBA-F2cos30°+Fsin30°=0」 ∫Fa=-0.366 得 E5=0Fac-F2os60°-Reos30°=0 E=1.366P Fa0F 有:F=F=P (分析:应如何选择坐标轴) 结果所得“一”号说明力的实际指向与假设相反 思考:「①此题结果是否与B轮尺寸有关? 〔②还可如何选取研究对象? 例: a a 求:A、B两处反力 法1、解析法、(注意AC为二力构件,并注意应用“三力平衡汇交”) 分析整体(也可BC)区五,=0F-Pcos45=0 法2、几何法: 5名之分析整体,应用力多边形自行封闭F=FB=号P 注:在应用几何法中若力的指向假定相反, 则应再选择力的指向继续画图。 作业:1-2:(c、(e) 2-3
4 (分析:应如何选择坐标轴) 例: 有: F1 F2 P 求:平衡时 AB、BC 两杆的受力(忽略摩擦、绳和杆自重,不计B轮尺寸!!) 是否必要?! 解:轮B(忽略大小,视为一点,即:实际是将轮B视为销钉) (注意:AB、BC 均为二力构件) 0 0 y x F F cos 60 cos30 0 cos30 sin 30 0 1 1 F -F F -F -F F BC 2 BA 2 得 F = P F = P BC BA 1.366 0.366 结果所得“—”号说明力的实际指向与假设相反 思考: ①此题结果是否与B轮尺寸有关? ②还可如何选取研究对象? 求:A、B两处反力 法1、解析法、(注意 AC 为二力构件,并注意应用“三力平衡汇交”) 分析整体(也可 BC) F o F o y x F -P o F -P o A B cos 45 cos 45 得 B A F F 法2、几何法: 分析整体,应用力多边形自行封闭 F F 2 P 2 A B 注:在应用几何法中若力的指向假定相反, 则应再选择力的指向继续画图。 作业:1-2:(c)、(e) 2-3 P 例: