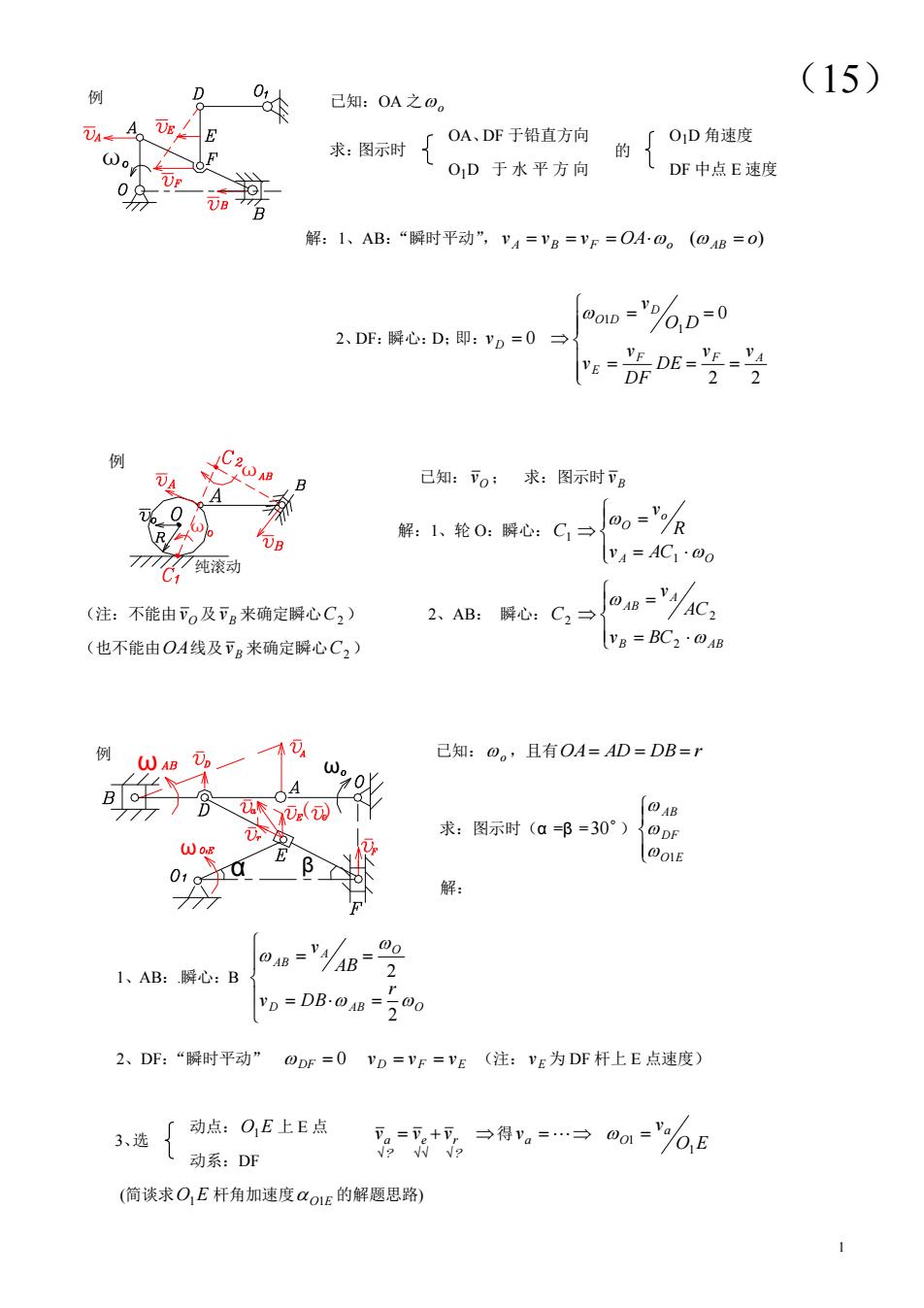
例 D 0在 (15) 已知:OA之0。 。A, E 求:图示时厂OA、DF于铅直方向 的厂OD角速度 OD于水平方向 DF中点E速度 解:1小、AB:“解时平动”VA=Vg=yF=OA。(AB=o) -00 2、DF:瞬心:D:即:=0→ 例列 已知:下o:求:图示时下g 纯滚动 vA=AC1·oo (注:不能由下o及下B来确定瞬心C2) 2、AB:瞬心:C2→ -/AC: (也不能由OA线及下B来确定瞬心C2) yB=BC2·OAB 例 已知:O。,且有OA=AD=DB= A 求:图示时(aB=30°)00F QOIE 01g 解: 1、AB:瞬心:B Yp=DB-0AB-700 2、DF:“瞬时平动”DF=0VD=VF=VE(注:VE为DF杆上E点速度) =+5→得,=日0a=6E (简谈求O,E杆角加速度αo1e的解题思路)
1 2、DF:瞬心:D;即: 2 2 0 0 1 1 F F A E D O D D v v DE DF v v O D v v 2、AB: 瞬心: B AB A AB v BC AC v C 2 2 2 解:1、轮 O:瞬心: A O o O v AC R v C 1 1 求:图示时(α =β = 30 ) O E DF AB 1 1、AB:.瞬心:B D AB O A O AB r v DB AB v 2 2 3、选 已知:OA 之 o OA、DF 于铅直方向 O1D 角速度 O1D 于 水 平 方 向 DF 中点 E 速度 解:1、AB:“瞬时平动”, v v v OA ( o) A B F o AB 已知: O v ; 求:图示时 B v (注:不能由 O v 及 B v 来确定瞬心 C2 ) (也不能由 OA 线及 B v 来确定瞬心 C2 ) 已知: o ,且有 OA AD DB r 解: 2、DF:“瞬时平动” DF 0 D F E v v v (注: E v 为 DF 杆上 E 点速度) 动点: O1E 上 E 点 动系:DF (简谈求 O1E 杆角加速度 O1E 的解题思路) ω 的 例 ω ω 例 纯滚动 α ω β ω ω ( ) 例 (15) 求:图示时 (15) ? e r ? a v v v 得 O E v v a a O 1 1

求:VDE E必 巴考 77 选厂动点:O4上A点 01 C动系:BD ,(健在于如何确定。方向 B 例R 己知:vA D 求:图示时08(注:法1:可应用点合成运动方法复习》 77A7 解:AB→确定瞬心C(关键!也是难点) §8-4用基点法求平面图形内各点的加速度 B B a 选基点:A a A 随基点A平移 绕基点A转动 己知:{0求:ag a,:牵连加速度 āa4:相对加速度 一般写法:ag=a4+aB4+a a8 =BA-a →aaM=aB4+aRd aB =BA.02 基点法求加速度公式:aB=a4+a+aR 注::牵连运动是随基点的平动(随平动参考系的平动) :“基点法求加速度公式中无点的合成公式中的科氏加速度ā。!
2 选 ? r ? a e v v v (关键在于如何确定 e v 方向) 求: DE v 动点: O1A 上 A 点 动系:BD 已知: A v 解:AB 确定瞬心 C(关键!也是难点) §8-4 用基点法求平面图形内各点的加速度 基点法求加速度公式: n BA t aB aA aBA a 注:∵牵连运动是随基点的平动(随平动参考系的平动) ∴基点法求加速度公式中无点的合成公式中的科氏加速度 c a !! ω 思考 ω α ω α ω α ω 选基点: + ω 例 求:图示时 B AB v (注:法 1:可应用点合成运动方法(复习)) 已知: A a 求: B a 随基点 A 平移 A a :牵连加速度 绕基点 A 转动 aBA :相对加速度 2 a BA a BA n BA t BA n BA t aBA aBA a aB aA aBA 一般写法: n BA t aB aA aBA a
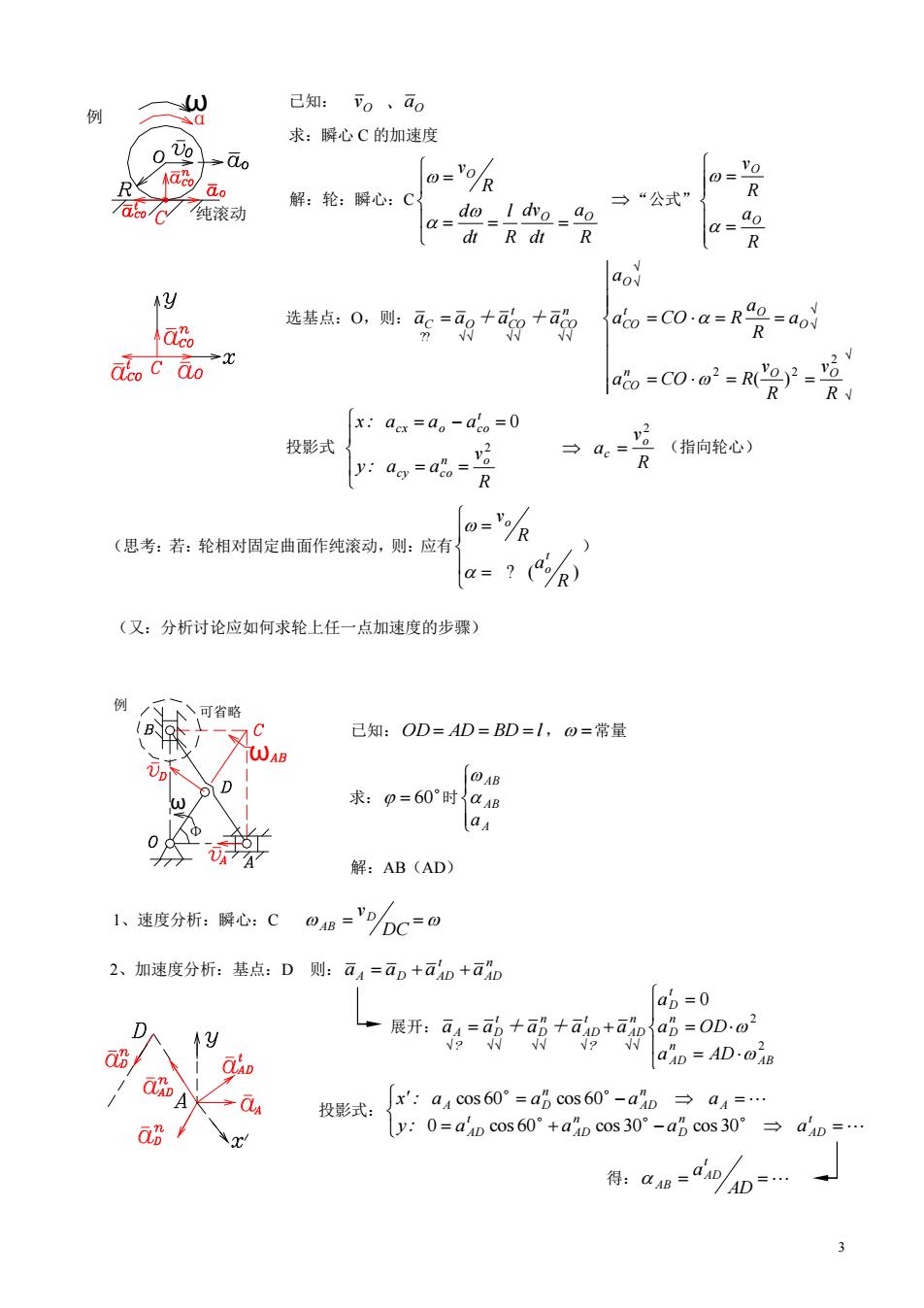
已知:0、a0 求:解心C的加速度 石纯滚动 解:轮:瞬心:C o-Y9R →“公式” a do I dvo ao dRd山R a=9o R y 选基点:0则:g++ cik c ao x:dex=do-aco=0 投影式 6是 (指向轮心) (您考:右轮相时因定角面作纯我动,贴:应动-次 a-70) (又:分析讨论应如何求轮上任一点加速度的步骤) /入可省略 C 已知:OD=AD=BD=I,=常量 D QAB 求:p=60°时aB a 解:AB(AD) 1、速度分析:瞬心:CoB='C=0 2、加速度分析:基点:D则:a4=aD+aAD+ā ap=0 y 展开:a=+可++a心=00. ap AD.@B amAa 投影式: Jx':a4cos60°=ap cos60°-aD→a4=… y:0=60'+s30°-a6cos30°→a=…
3 选基点:O,则: n CO t aC aO+aCO+a ?? R v R v a CO R a R a a CO R a n O O CO O t O CO O 2 2 2 ( ) 解:轮:瞬心:C R a dt dv R l dt d R v O O O “公式” R a R v O O 求: 60 时 A AB AB a 展开: 2 2 0 AB n AD n D t D n AD ? t AD n D t D ? A a AD a OD a a a + a + a a 已知: O 、 aO v 求:瞬心 C 的加速度 (又:分析讨论应如何求轮上任一点加速度的步骤) 已知: OD AD BD l , 常量 解:AB(AD) 2、加速度分析:基点:D 则: n AD t aA aD aAD a ω α 纯滚动 例 Φ ω ω 例 可省略 投影式 R v y: a a x: a a a n o cy co t cx o co 2 0 R v a o c 2 (指向轮心) (思考:若:轮相对固定曲面作纯滚动,则:应有 ? ( ) R a R v t o o ) 1、速度分析:瞬心:C DC vD AB 投影式: t AD n D n AD t AD A n AD n A D y: a a a a x : a a a a 0 cos 60 cos 30 cos 30 cos 60 cos 60 得: AD a t AD AB

B D. 已知:01=常量,OA=O,B=r,AB=1 例 AB杆 45°2 0 O:求:图示时 W, a 解:AB杆 1速度分析:基点:Λ(他可用心法十形a=V=os45由 a4→oB=ayA8 →m-6B 2、加速度分析:基点:A、则:ag=a4+a+a84 展开 形+酯=+a++a聪 ag=O2B·m a=0 投影式 x:ag=-a cos45°-adat→aa=…→aa=… B a a1=04o y:ag=acos45°-a4→a6=…-a,=… aB=AB.OiB 已知:01、41 例 个WeB a> AB B 解:AB杆 小、速度分析、瞬心:0,0B='0,=0→g=0B:0B→@='%,B 2加速度分折,基点A.ag=a+a4+a开+=耐+耐++ A 投影式:x:a cos p-=asinp-a4cosp-a ā 中 踏_x 儿得:=→-6B ā (若求aB,可选择x'轴投影求da1→aB) 作业:8-10,8-18
4 求:图示时 2 2 2 O B杆 AB杆 AB AB 求:图示时 2 2 2 o B (或再求 AB AB AB ) 已知: 1 常量, O A O B r, AB l 1 2 解:AB 杆 已知: 1 、1 解:AB 杆 投影式: n BA t A n A t B n x : aB cos a sin a sin a cos a ( (若求 AB ,可选择 x 轴投影求 AB t aBA ) 作业:8-10,8-18 ω ω ω 例 α ω ω φ 例 ω φ 1、速度分析:基点:A(也可用瞬心法), ? A BA ? B v v v vB vBA vA cos 45 由 O B v v AB v v B B BA BA AB 2 2 2、加速度分析: 基点:A、则: n BA ? t BA n A t A n B ? t B n BA t aB aA aBA a a a a a a a 展开 2 2 1 1 2 2 2 0 AB n BA n A t A n B a AB a O A a a O B 投影式 45 2 cos cos 45 t B n BA n A t B BA t BA t BA n A n B y: a a a a x: a a a a 1、速度分析、瞬心: O1, O B v v O B AO v B B AB A AB 2 1 1 2 1 2、加速度分析、基点 A . n BA ? t BA n A t A n B ? t B n BA t aB aA aBA a 展开 a a a a a a 得: O B a a t t B B 2 2