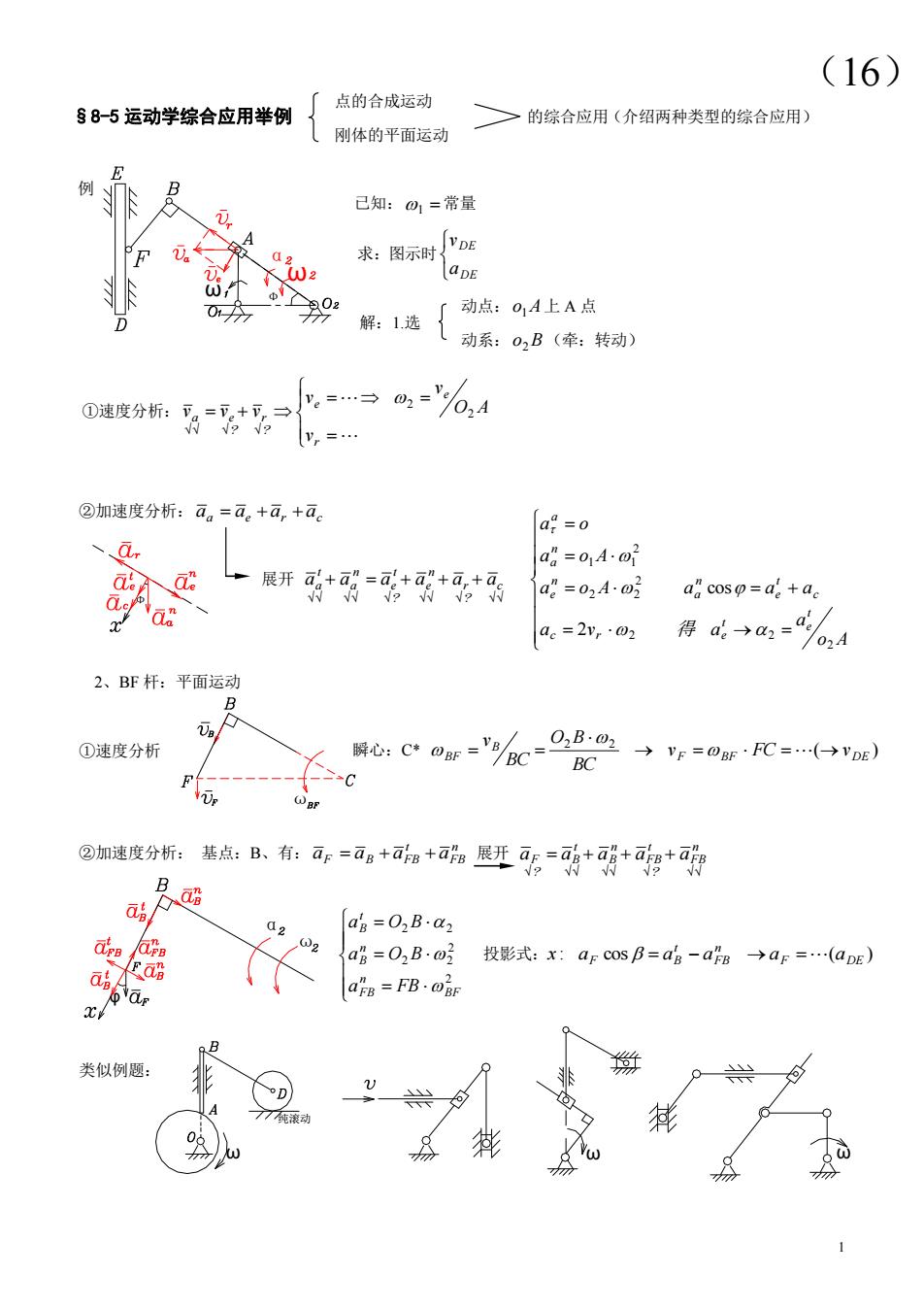
(16) $85运动学综合应用举例 「点的合成运动 >的综合应用(介绍两种类型的综合应用) 〔刚体的平面运动 例 己知:0,=常量 02 求:图示时aE 99 ①速度分析:为=+7。→ .=…=y%,A ②加速度分析:a。=a。+a,+ae a=o a8=0A02 中展开耐+弱可形a对+。 a=02A.02 a cosp-a。+ae ae=2m,02 得da-% 2、BF杆:平面运动 ①速度分析 BC +C ②加速度分析:基点:B、有:a=as++码展开g=砖+a醋+可+ a/ as=02B.az ①2 a8=02B·o3 投影式:x:aF cosB=ag-aFB→ar=(apE) aB=FB·o 类似例圈
1 Φ 投影式 x §8-5 运动学综合应用举例 展开 o A a a v 得 a a o A a a a a o A a o a a a a a a t e t c r e c t e n a n e n a a c ? r n e ? t e n a t a 2 2 2 2 2 2 2 1 1 2 cos 求:图示时 DE DE a v ①速度分析: r e e ? r ? a e v O A v v v v v 2 2 点的合成运动 刚体的平面运动 已知: 1 常量 动点: o1A 上 A 点 动系: o2B (牵:转动) ②加速度分析: aa ae ar ac 2、BF 杆:平面运动 ①速度分析 ②加速度分析: 基点:B、有: n FB t aF aB aFB a 展开 n FB ? t FB n B t B ? aF a a a a 类似例题: α ω Φ ω 例 (16) 的综合应用(介绍两种类型的综合应用) 解:1.选 瞬心:C* ( ) 2 2 F BF DE B BF v FC v BC O B BC v ω 2 2 2 2 2 2 BF n FB n B t B a FB a O B a O B 投影式: : cos ( ) F DE n FB t x aF aB a a a α φ ω 纯滚动 ω ω ω

已知:滑块VE=常量 B D 45 OBD杆厂'D (增加该第①间) 求:图示时 OA E ②0A杆 解:1、机构BDE,分析BE杆:平面运动 B 2% 米D ①速度分析,瞬心:C(恰好为0点) OE-'0→vg=OB.OaE(→vaD) 中0客D ②加速度分析,基点:,有:ag=0+g+形 ∫aE=0 dis =BE-OnE 礼E 投影式:x:ag cos45°=aBE→得ag→aD 2、分析机构ABD, B {整m牌的我 ,=0 ①滤度分折:怎=怎 8元 有:。=VD得 个“oa aa=aBD ②加速度分析:可,=a+a,+a。展开a,=d+a+a+a,有a=0B:0i a:=2y,·o64=0 aa。龙a=-d。→aou=%B 日马。思考题:A、B两点加速度在其两点连线上的投影 相等的充、要条件是①)=0②a=0?(判断) (由:ag=a4+aM+a很进行判断) 2
2 BD v aBD ①BD 杆 OA OA ②OA 杆 ②加速度分析: aa ae ar ac 展开 c ? r n e ? t aa ae a a a 有 2 0 2 2 c r OA OA n e a BD a v a OB a a 思考题: A、B 两点加速度在其两点连线上的投影 相等的充、要条件是① 0 ;② 0 ?(判断) (由: n BA t aB aA aBA a 进行判断) 已知:滑块 E 常量 解:1、机构 BDE,分析 BE 杆: 平面运动 投影式: x : aB cos 45 aBE n 得 aB aBD 动点:BD 上的 B 点(或滑块 B) 动系:OA(牵:转动) 例 求:图示时 (增加该第①问) ②加速度分析,基点:E,有: n BE ? t E BE ? aB a a a aE 0 2 BE n aBE BE ω ①速度分析,瞬心:C(恰好为 O 点) EO vE BE ( ) B BE BD v OB v 2、分析机构 ABD, 选 ①速度分析: ? r ? a e v v v 有 : a BD v v 得 OB v v v v e e a OA r 0 ω 有: a BD v v 得 OB v v v v e e a OA r 0 OB a a a t e OA t a e
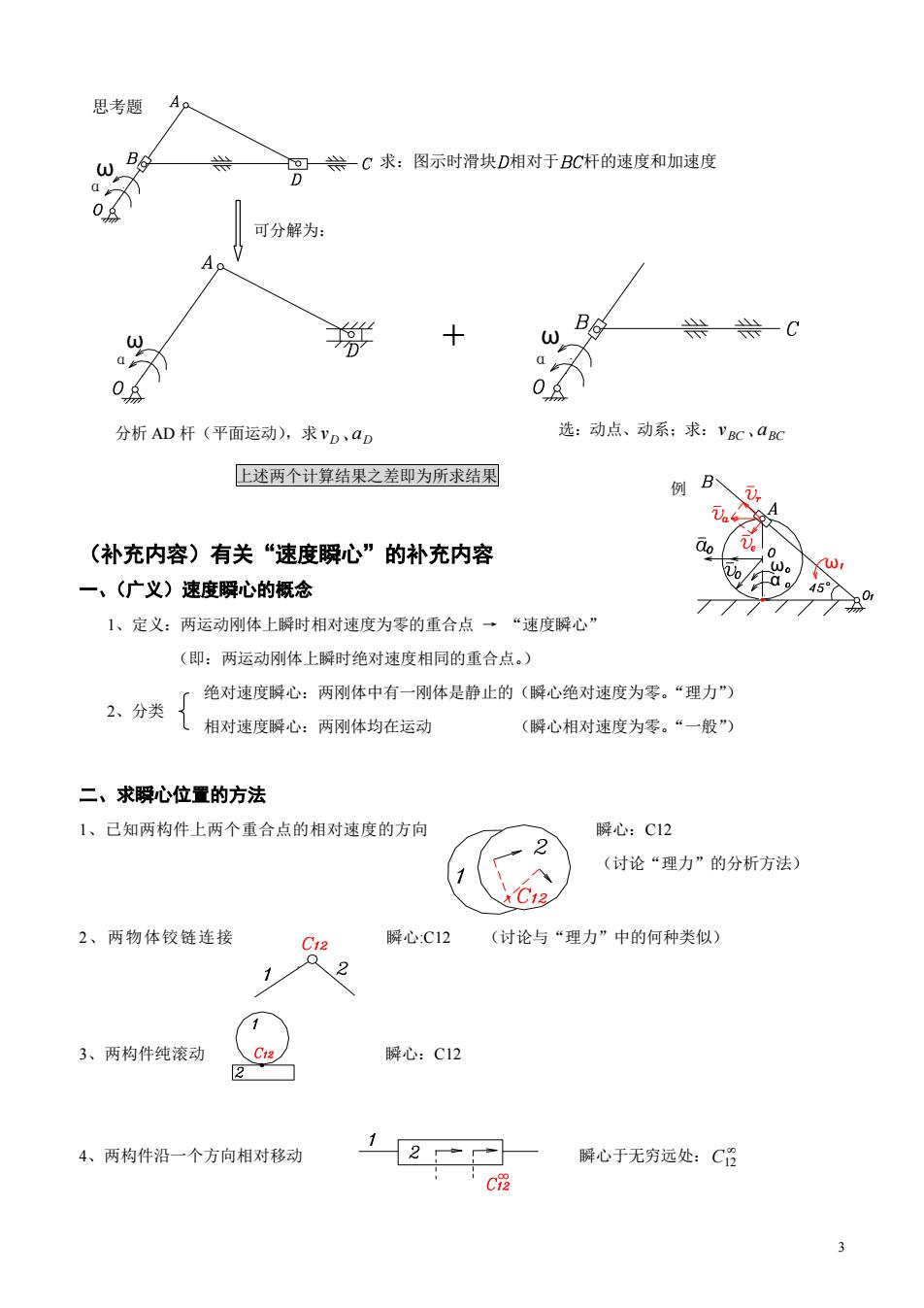
思考题 。C求:图示时滑块D相对于BC杆的速度和加速度 可分解为: 分析AD杆(平面运动),求VD,ap 选动点、动系:求:VC,aC 上述两个计算结果之差即为所求结果 例B (补充内容)有关“速度瞬心”的补充内容 一、(广义)速度瞬心的概念 1、定义:两运动刚体上瞬时相对速度为零的重合点一“速度瞬心” (即:两运动刚体上瞬时绝对速度相同的重合点。) 之、分类厂绝对速度厚心:两刚体中有-体是静止的(偶心绝对速度为零。“男力 儿相对速度瞬心:两刚体均在运动 (瞬心相对速度为零。“一般”) 二、求瞬心位置的方法 1、己知两构件上两个重合点的相对速度的方向 解心:C12 2 (讨论“理力”的分析方法》 ℃13 2、两物体铰链连接 C12 降心:C12 (讨论与“理力”中的何种类似) 1 、2 3、两构件纯滚动 瞬心:C12 2 4、两构件沿一个方向相对移动 12 解心于无穷远处:C日
3 ω α ω 例 上述两个计算结果之差即为所求结果 (补充内容)有关“速度瞬心”的补充内容 一、(广义)速度瞬心的概念 1、定义:两运动刚体上瞬时相对速度为零的重合点 → “速度瞬心” (即:两运动刚体上瞬时绝对速度相同的重合点。) 绝对速度瞬心:两刚体中有一刚体是静止的(瞬心绝对速度为零。“理力”) 相对速度瞬心:两刚体均在运动 (瞬心相对速度为零。“一般”) 二、求瞬心位置的方法 1、已知两构件上两个重合点的相对速度的方向 瞬心:C12 (讨论“理力”的分析方法) 2、两物体铰链连接 瞬心:C12 (讨论与“理力”中的何种类似) 3、两构件纯滚动 瞬心:C12 4、两构件沿一个方向相对移动 瞬心于无穷远处: C12 思考题 ω α 求:图示时滑块 相对于 杆的速度和加速度 可分解为: α ω 分析 AD 杆(平面运动),求 D 、aD v ω α 选:动点、动系;求: BC 、aBC v + 2、分类

5、构件构成滑动兼滚动 瞬心C12位于过接触点的公法线N上(具体位置待定) (简述小车的“ABS”) (相对速度沿切线方向) 三、运动机构瞬心的数目 厂N:瞬心数目 K:机构构件数目 四:“三心定理”:作平面运动的三个构件共有三个瞬心,且为于同一直线上 证明:机构瞬心数目:N=弓3-)=3 瞬心了C3: >绝对速度瞬心 3 C23: 一相对速度瞬心 由“三心定理”:C12、C、C2必位于同一直线上 777717 证明:只有当构件和3的重合点A在C12与C的连线上时 才可能使构件2和3上的重合A的绝对速度方向一致(即:2与3方向一致) 注:C23位于C12和C3两点连线上的具体位置还需考虑2、3的转向及大小。 C13 例 试确定四连杆机构的瞬心 C 绝对速度瞬心 C /3 C34 0瞬心数目N-4-)=6 C23 C1/A D C24相对速度瞬心 C3) 「构件1、2、3的三个心位于同一直线 1构件1、4、3的三个瞬心位于同一直线 >交点C3 ②应用“三心定理”求 C24 「构件2、3、4的三个瞬心位于同一直线 构件2、1、4的三个瞬心位于同一直线 >交点C24 例: 构件2、3构成滚动兼滑动 Ws 2 N [C2 C23 作业:8-25,8-2 4
4 瞬心 ①瞬心数目 (4 1) 6 2 4 N 14 13 12 C C C 绝对速度瞬心 34 24 23 C C C 相对速度瞬心 5、构件构成滑动兼滚动 瞬心 C12 位于过接触点的公法线 N 上(具体位置待定) (简述小车的“ABS”) (相对速度沿切线方向) 三、运动机构瞬心的数目 N:瞬心数目 K:机构构件数目 四:“三心定理”:作平面运动的三个构件共有三个瞬心,且为于同一直线上。 证明: 机构瞬心数目: (3 1) 3 2 3 N C12 : C13: C23: — 相对速度瞬心 由“三心定理”: C12 、C13、C23 必位于同一直线上。 证明:只有当构件和 3 的重合点 A 在 C12 与 C13 的连线上时, 才可能使构件 2 和 3 上的重合 A 的绝对速度方向一致(即: u A2 与 u A3 方向一致) 注: C23 位于 C12 和 C13 两点连线上的具体位置还需考虑 2 、3 的转向及大小。 试确定四连杆机构的瞬心 构件 2、3 构成滚动兼滑动 作业:8-25, 8-29 ω ω 例: ω ω 例: ( 1) 2 K K N 绝对速度瞬心 交点 C13 构件 1、2、3 的三个瞬心位于同一直线 构件 1、4、3 的三个瞬心位于同一直线 交点 C24 构件 2、3、4 的三个瞬心位于同一直线 构件 2、1、4 的三个瞬心位于同一直线 ②应用“三心定理”求 C13 C24 23 13 12 C C C