北京化工大学：《理论力学》课程教学资源（教案讲义）第九章 质点动力学的基本方程、第十章 动量定理 §10-1 动量与冲量 §10-2 动量定理

(17) 动力学（研究物体机械运动与作用力之间的关系） (相对静力学及运动学而言，动力学是研究机械运动更一般规律的科学) 厂静：仅研究平衡问题 运：仅研究运动几何性质 力学模型 了质点 了质点动力学 质点系 了不变质点系 质点系动力学 可变质点系 “重点”（且重点为：刚体或刚体系统动力学问题） 第九章质点动力学的基本方程 (介绍要点，复习自学) §91、动力学基本定律：牛倾三定律，(“古典力学”) (①惯性定律、②力与加速度关系定律、③作用与反作用关系定律) 其中：ma=下“动力学基本方程” 惯性参考系：牛顿三定律适用的参考系（一般工程问题 了①周连于地球上的参考系 ·②周连于相对地球匀速直线运动物体上的参考系 §9-2、质点的运动微分方程 -Σ 1、矢量形式：ma=F或m版=∑F→ d'r-EF m d mdj-EF "dr 2、直角坐标形式： y =∑Fa(或：m d's =∑Fn) dt- >注：全加速度：a=a,+an 3、自然坐标形式： m (a6=0) 0=ΣF ①力为常力 4、质点动力学的两类基本问1、已知运动，求力(“正”问题，较简单 ②力为时间的函数 2、已知力，求运动(“逆”问题，较难)， ③力为速度的函数 3、上两类的综合题 ④力为位置的函数

1 1、矢量形式： ma  F 或 ma   Fi             i i F dt d r m F dt dv m 2 2 2、直角坐标形式：            z y F dt d x m 2 xi 2 ①力为常力 ②力为时间的函数 ③力为速度的函数 ④力为位置的函数 动力学（研究物体机械运动与作用力之间的关系） （相对静力学及运动学而言，动力学是研究机械运动更一般规律的科学） “重点”（且重点为：刚体或刚体系统动力学问题） 第九章 质点动力学的基本方程 （介绍要点，复习自学） §9-1、动力学基本定律： 牛顿三定律， （“古典力学”） （①惯性定律、②力与加速度关系定律、③作用与反作用关系定律） 其中： ma  F “动力学基本方程” 惯性参考系：牛顿三定律适用的参考系（一般工程问题 §9-2、质点的运动微分方程 4、质点动力学的两类基本问题 1、已知运动，求力（“正”问题，较简单） 2、已知力，求运动（“逆”问题，较难）， 3、上两类的综合题 （17） 静：仅研究平衡问题 运：仅研究运动几何性质 质点 质点系 不变质点系 可变质点系 力学模型 质点动力学 质点系动力学 ①固连于地球上的参考系 ②固连于相对地球匀速直线运动物体上的参考系 3、自然坐标形式：                    bi ni ti ti F F v m F dt d s F 或 m dt dv m 0 ( : ) 2 2 2  注：全加速度： a  at  an （ ab  0 ）

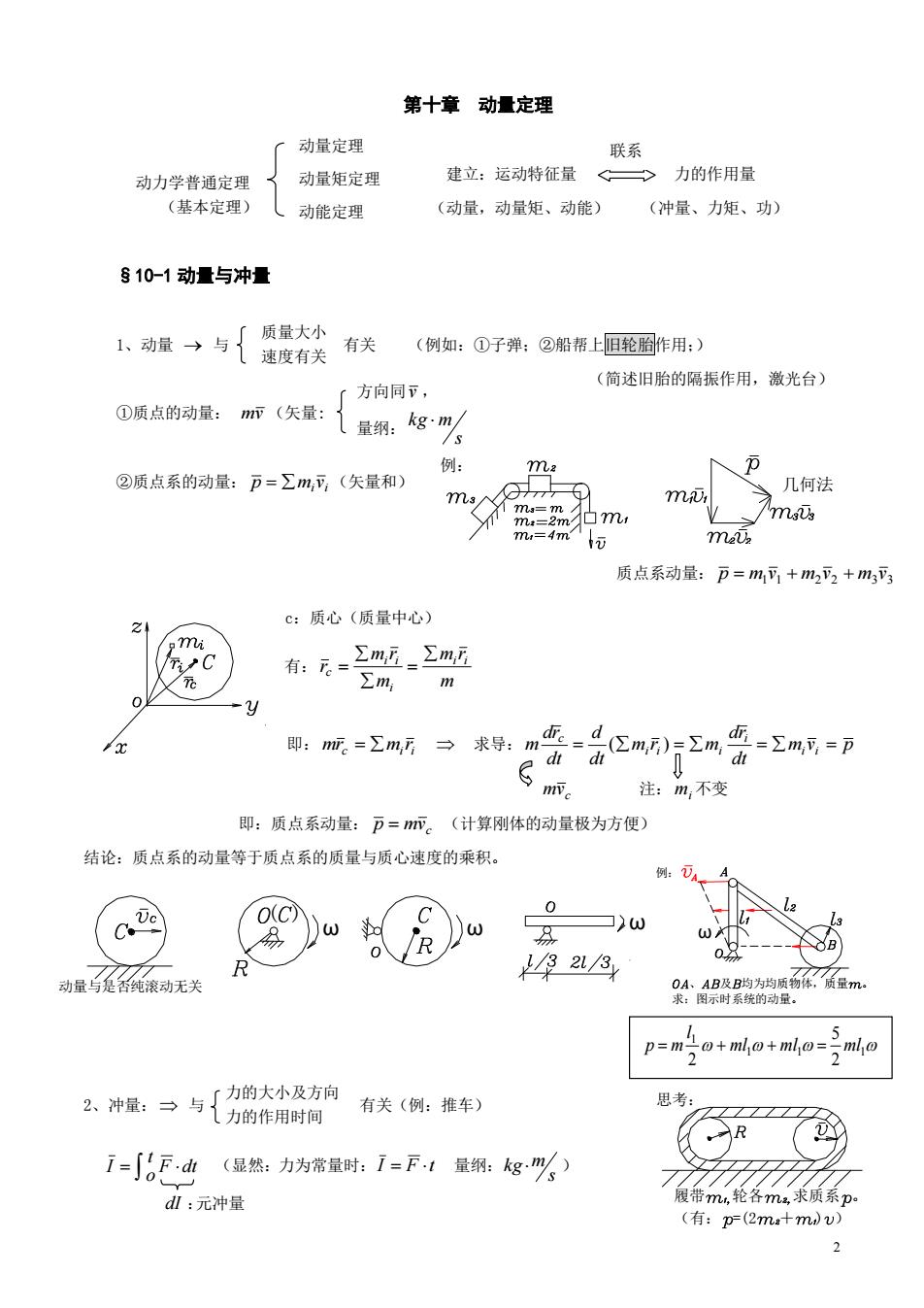
第十章动量定理 动量定理 联系 动力学普通定理 动量矩定理 建立：运动特征量一>力的作用量 (基本定理 动能定理 (动量，动量矩、动能) (冲量、力矩、功) 810-1动量与冲量 1、商量→与{数资关 有关（例如：①子弹：②船帮上旧轮丽作用：） (方向同下， (简述旧胎的隔振作用，激光台) ①质点的动量：m(矢量：{量绑：kgm 例： m: ②质点系的动量：=∑m,可（矢量和） m 几何法 =m Amits m=4m 1m, 元 m元 质点系动量：币=m可+m22+m3 c:质心（质量中心） 有：元。 ∑m正_∑m正 ∑m, m :m.=工m听三求2市立（区mm或=Σm可=D 注：m,不变 即：质点系动量：下=m。(计算刚体的动量极为方便) 结论：质点系的动量等于质点系的质量与质心速度的乘积。 323 动量与是否纯滚动无关 p=m子+mlo+mlo-ml 思考： R 1=∫F山（显然：力为常量时：1=F1量纲：kg%) d:元冲量 履带m,轮各m2求质系p (有：pr(2ma+mdv) 2

2 联系 有： m m r m m r r i i i i i c      即： c i i mr  m r  求导： m v p dt dr m r m dt d dt dr m i i i i i i c  ( )      力的大小及方向 力的作用时间 dI ：元冲量   F dt o t I （显然：力为常量时： I  F t 量纲： s kgm ）  1 1 1 1 2 5 2 ml ml ml l p  m    思考： 履带 轮各 求质系 。 （有： =(2 ＋ ) ） 第十章 动量定理 建立：运动特征量 力的作用量 （动量，动量矩、动能） （冲量、力矩、功） §10-1 动量与冲量 1、动量  与 有关 （例如：①子弹；②船帮上旧轮胎作用；） （简述旧胎的隔振作用，激光台） ①质点的动量： mv （矢量: ②质点系的动量： i i p  m v （矢量和） c：质心（质量中心） c mv 注： mi 不变 即：质点系动量： c p  mv （计算刚体的动量极为方便） 结论：质点系的动量等于质点系的质量与质心速度的乘积。 2、冲量：  与 有关（例：推车） 例： 几何法 ( ) ω ω ω 动量与是否纯滚动无关 动量定理 动量矩定理 动能定理 动力学普通定理 （基本定理） 质量大小 速度有关 方向同 v ， 量纲： s kg  m 质点系动量： 1 1 2 2 3 3 p  m v  m v  m v ω 、 及 均为均质物体，质量 。 求：图示时系统的动量。 例：

§10-2动量定理 「d 质点的动量定理：由：m版=F→m乐=F→市m)厂 “微分形式“ d(m)=F.d山（动量增量等于力的元冲量） 上式积分：得：m-m。=∫F·=1“积分形式”（动量的变化等于力的冲量》 2、质点系的动量定理： “外力”内力 对系统内第i个质点：有d(m,)=F·d=(+F)d=dh+Fd 对整个系统：有∑d(m,,)=∑F°·dh+∑E·d山 d∑m,可，=Φ 0 do-∑Fedh-∑dl 质点系动量的增量等于外力元冲量的矢量和： 微分形式 {屯=ΣF外力主质点系动最对时间的导数等于外力的矢量和（住） 积分形式：（有限形式）下-。=∑：质点系动量的改变量等于外力冲量的矢量和 (注：动量定理为矢量形式解题时取投影式) 迎：=ΣF Px-Pm=∑IE 微分形式{y 积分形式 y 3、质点系动量守恒定律 「若：∑°=0，则币=常矢量 简：“外力主矢为零，动量不变” (若：∑F=0,则P=常量 已知：船重W,人重Q,初始船速（人相对船不动） 某瞬时人相对船以可，行走。 二Nm不计水阻 求：此时船速2 解：研究整体（人和船组成的质点系） (解题步骤：①研究对象：②受力及运动分析：③运用适当定理求解 受力和运动分析：∑F=0“质点系P.=常量（水平方向动量守恒》 >有P1=P2,得，=yW十0 W P2= ,2十，)（注意：此时牵连速度应为，） (举例)

3 1、质点的动量定理：由：             d mv F dt mv F dt d F dt dv ma F m ( ) ( ) “外力” ”内力” 微分形式          z y F dt dp e x x 积分形式         z y p p I e x ox x dm v  dp 0 i i §10-2 动量定理 2、质点系的动量定理： 对系统内第 i 个质点：有 d m v F dt F F dt F dt F dt i i e i i i e ( i i )  i   ( i  )   对整个系统：有 d m v F dt F dt i i e i i i  ( )       即 积分形式：（有限形式） e o i p  p   I ：质点系动量的改变量等于外力冲量的矢量和 （注：动量定理为矢量形式 解题时取投影式） 3、质点系动量守恒定律 若：   0 e Fi ，则 p  常矢量 若：   0 e Fx ，则 px  常量 已知：船重 W ，人重 Q ，初始船速 1 v （人相对船不动） 某瞬时人相对船以 r v 行走， 求：此时船速 2 v 解：研究整体（人和船组成的质点系） （解题步骤：①研究对象；②受力及运动分析；③运用适当定理求解） 受力和运动分析：∵ F o e  x  ∴质点系 px  常量（水平方向动量守恒） （举例） “微分形式“ （动量增量等于力的元冲量） 简：“外力主矢为零，动量不变”。 例： 不计水阻 上式积分：得：    F  dt  I o t mv mvo “积分形式”（动量的变化等于力的冲量） e i e i dp   F dt  dI 质点系动量的增量等于外力元冲量的矢量和； e Fi dt dp   (“外力主矢”)：质点系动量对时间的导数等于外力的矢量和(主矢) 微分形式 1 1 v g W Q px   ( ) x2 2 2 r v v g Q v g W p    （注意：此时牵连速度应为 2 v ） 有 px1  px2 ，得 r v W Q Q v v  2  1 

初始系统静止，p=p。 A只 -产杆释放后，近似以p=p。cos规律摆动 中L光滑水平面 求：物块A的最大速度 m B 解：分析整体 :∑F=0·Px=常量=0(：初始静止)（水平方向动量守恒） 即：m心+mBy=0→myA+mB(yA-ym)=0(有：，=Io) 得：AmA+mB mRV 分析：当p=0时，Va最大，即：(vn)m=l=lop。 得：(wm=m+m。 mlop。 例：可@ 设：流体为不可压缩的理想流休，且稳定流动（定常） 流体密度为p,单位时间体积流量为q外(Q) 求：管壁的附加动约束反力 h F 解：分析aa与bb之间的流体（质点系） t:aa~bb间 {+:aa-b6同 dt时间内质点系动量的变化为：而-Paih1一Pb=(Ph1+Pa16)-(paib+pml) 流动是稳定的∴paib=Pib即：而=p1一pl 也即：d=(Qn)pb-(Qpdi)币a=Qp-下a)dl h=0p。-) 即： 又由质点果动量定里车-工→0)丽+后+反+灯 “欧拉方程”（稳定流的动量方程） 【产：动反附加动反力一：有：币+E+厅+刀=0 约束反力：N=N'+N”「N':静反力 得：N"=Qp。-a)=gp。-) 例：求：附加动反力 x:N=gp(y2-0)=p4 由N”=qp(下。-)→投影式： y:Ng=gp0-(-y》=p4, (注：=4=42)（分折：即使"？，也存在动反力） 4=A2 (另思考：为何有拐弯圈的原因)作业：思考题中：10-1：习题：10-3、10-7 4

4 又：由质点系动量定理：   Fi e  dt dp Q(vb  va ) W  Fa  Fb  N N  ：静反力 N  ：动反力(附加动反力) （分析：即使      1 2 1 2 A A v v ，也存在动反力） 得： A B B rx A m m m v v   得： A B B o A m m m l v    max ( ) 初始系统静止，   o 杆释放后，近似以 t  o cos 规律摆动。 求：物块 A 的最大速度 解：分析整体 ∵ F o e  x  ∴ px  常量  0 (∵初始静止)（水平方向动量守恒） 即： mA vAx  mB vBx  0  mA vA  mB (vA  vrx )  0 （有： v l  r  ） 分析：当   0 时， rx v 最大，即： rx o (v )max  l  max  l 设：流体为不可压缩的理想流体，且稳定流动（定常） 流体密度为  ，单位时间体积流量为 qv （ Q ） 求：管壁的附加动约束反力 解：分析 aa 与 bb 之间的流体（质点系）， dt 时间内质点系动量的变化为： ( ) ( ) dp pa1b1 pab pbb1 pa1b pa1b  paa1       ∵流动是稳定的 ∴ pa1b pa1b   即： dp  pbb1  paa1 也即： dp Q dt v Q dt v Q v v dt b a b a  (  )  (  )  (  ) “欧拉方程”（稳定流的动量方程） 约束反力： N  N  N 例： 求：附加动反力 由 ( ) b a N  qv v  v （注： 1 1 21 2 qv  A v  A v ） （另思考：为何有拐弯圈的原因） 作业：思考题中：10-1；习题：10-3、10-7 例： 例： t : aa ～bb 间 t  dt ： a1a1 ～b1b1 间 即： ( ) b a Q v v dt dp    ∵有： W  Fa  Fb  N  0 ∴得： ( ) ( ) b a b a N  Q v  v  qv v  v  投影式：              2 1 1 1 2 2 2 2 (0 ( )) ( 0) y： N qv v A v x： N qv v A v y x     Φ 光滑水平面 例：