
(23) 第十三章达朗贝尔原理 要点:应用静力学中研究平衡问题的方法来研究动力学问题。“动静法” S13-1惯性力·质点的达朗贝尔原理 、万 m (FR=ma)有:ma=F+NF+N-ma=0 、下(生动力) 令:F,=-ma“质点惯性力” -ma 则有:F+N+万,=0“质点的达朗贝尔原理 (约束反力) 结论:作用在质点上的主动力、约束反力和假想的惯性力在形式上构成一平衡力系。 注意 厂女质点并未受到惯性力作用, (☆.“平衡力系”实际并不存在, [Fx+Nx+Fg=0 [F,+N:+Fn=0 投影式(直角坐标) 自然坐标 Fn+Nn+Fi=0 =0 注意 §13-2质点系的达朗贝尔原理 对某1质点,有:F+N,+F,=0(形式上“平衡”的汇交力系) 对整个系统,有:所有主动力,约束反力和惯性力在形式构成一平衡力系(空间任意力系) 对某i质点的:F+N,+F=0→F+F+F=0 F+F “外”“内 主矢为零:万+∑+∑FM=0 对质点系的空间任意力系的“平衡条件”,有: 主矩为零:∑M()+∑M()+∑M。(下)=0 ∑E+∑F,=o 又:质点系内力的性质“最后有: ∑M(E)+∑M(厘)=o Σ下4:惯性力系的主矢 ZF,=0 式中 对于平面问题,有:∑F,=0 ∑M。(正,):惯性力系的主矩 ∑M。=o (若为空间力系,则应有六个投影方程)
1 对质点系的空间任意力系的“平衡条件”,有: 又∵质点系内力的性质 ∴最后有: 式中: 对于平面问题,有: M o F o F o o y x 注意 投影式(直角坐标) z y Fx Nx FIx o 自然坐标 F N o F N F o F N F o b b n n In t t It 第十三章 达朗贝尔原理 要点:应用静力学中研究平衡问题的方法来研究动力学问题。“动静法” §13-1 惯性力·质点的达朗贝尔原理 ( FR ma )有: ma F N F N ma o 令: FI ma “质点惯性力” 则有: F N FI 0 “质点的达朗贝尔原理” 结论:作用在质点上的主动力、约束反力和假想的惯性力在形式上构成一平衡力系。 ☆.质点并未受到惯性力作用, ☆.“平衡力系”实际并不存在, §13-2 质点系的达朗贝尔原理 对某 i 质点,有: Fi Ni FIi o (形式上“平衡”的汇交力系) 对整个系统,有:所有主动力,约束反力和惯性力在形式构成一平衡力系(空间任意力系) 对某 i 质点的: Fi Ni FIi o F F FIi o i i e i 主矢为零: F F FIi o i i e i 主矩为零: M F M F Mo FIi o i o i e o ( i ) ( ) ( ) F FIi o e i M F Mo FIi o e o ( i ) ( ) FIi :惯性力系的主矢 ( ) Mo FIi :惯性力系的主矩 (若为空间力系,则应有六个投影方程) (23) i i e Fi F “外” “内” 注意 (主动力) (约束反力)
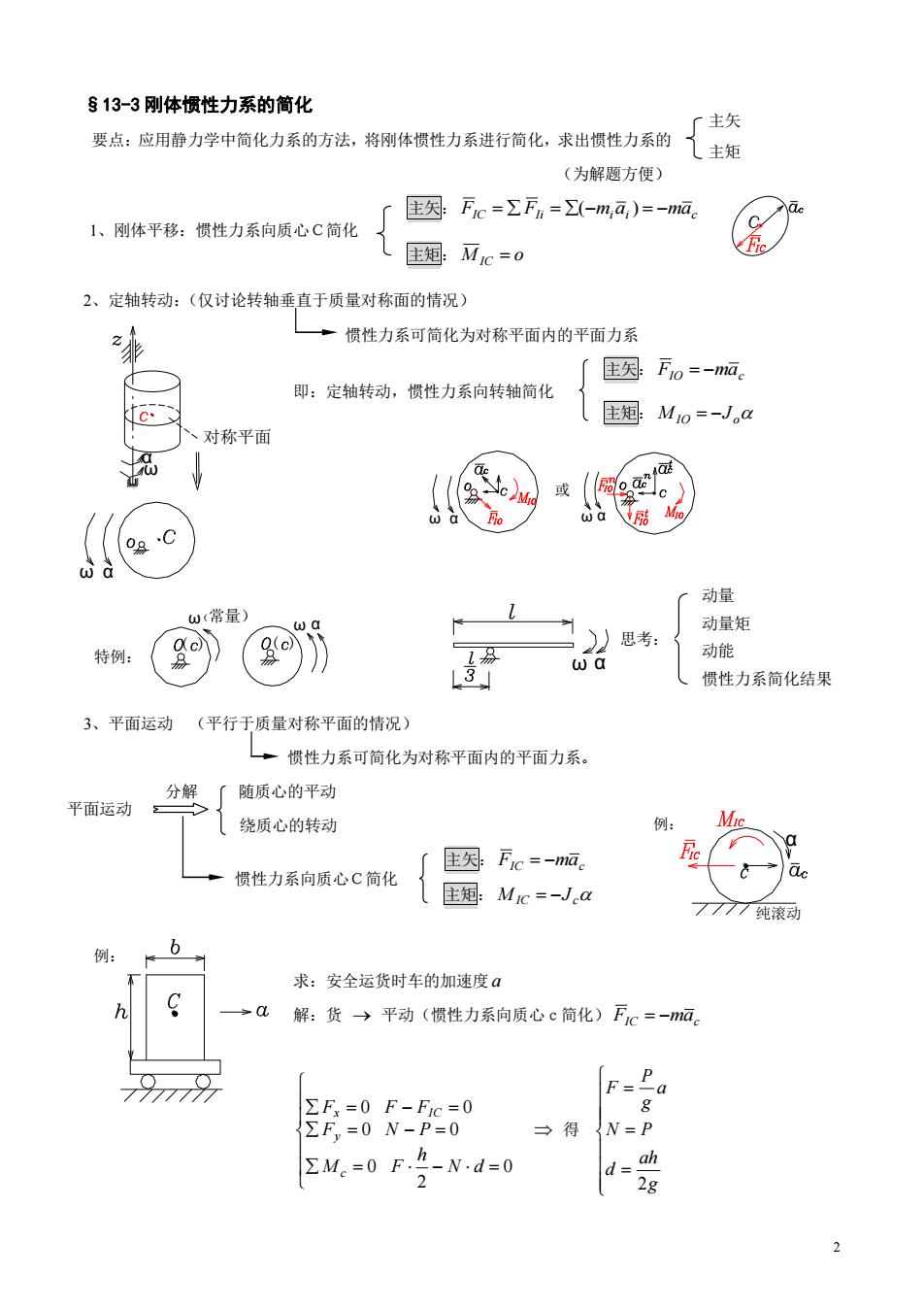
§13-3刚体惯性力系的简化 要点:皮用静力学中筒化力系的方法,将体损性力系进行筒化,求出候性力系的贰士软 (为解题方便) 主为Fe=ΣF6=Σ-m,a)=-ma 1、刚体平移:惯性力系向质心C简化 主想Mc=o 2、定轴转动:(仅讨论转轴垂直于质量对称面的情况) ·惯性力系可简化为对称平面内的平面力系 主因Fio=-ma。 即:定轴转动,惯性力系向转轴简化 c 矩Mo=-Ja 入对称平面 或 c à酷 动量 (常量 特例: &o9 动量矩 思考: w a 动能 (惯性力系简化结果 3、平面运动 (平行于质量对称平面的情况) 一惯性力系可简化为对称平面内的平面力系。 分解 「随质心的平动 平面运动 绕质心的转动 +惯性力系向质心C简化 住奥Fc=-ma。 主想:Mc=-JC 7777纯滚动 求:安全运货时车的加速度a 解:货→平动(惯性力系向质心c简化)Fc=-ma。 79 F-Pa ∑Fx=0F-Fc=0 ΣF,=0N-P=0 三得N=P EM,-0F空Nd-0 d= ah 2
2 主矢 主矩 ω α ω α 或 1、刚体平移:惯性力系向质心C简化 即:定轴转动,惯性力系向转轴简化 平面运动 惯性力系向质心C简化 §13-3 刚体惯性力系的简化 要点:应用静力学中简化力系的方法,将刚体惯性力系进行简化,求出惯性力系的 (为解题方便) 主矢: FIC FIi miai mac ( ) 主矩: M IC o 2、定轴转动:(仅讨论转轴垂直于质量对称面的情况) 惯性力系可简化为对称平面内的平面力系 主矢: FIO mac 主矩: M IO J o 3、平面运动 (平行于质量对称平面的情况) 惯性力系可简化为对称平面内的平面力系。 分解 随质心的平动 绕质心的转动 主矢: FIC mac 主矩: M IC Jc 求:安全运货时车的加速度 a 解:货 平动(惯性力系向质心c简化) FIC mac 0 2 0 0 0 0 0 N d h M F F N P F F F c y x IC 得 g ah d N P a g P F 2 ω ω α α 对称平面 α 纯滚动 例: 例: ( ) ω(常量) 特例: ( ) ω α ω α 思考: 动量 动量矩 动能 惯性力系简化结果

有f(时不医有- a P 不滑动:F≤N→a≤ 判断 >比较取小者 不翻倒:d≤号→a≤分8 W 47 例: 多 ∫a (绳拉力 c a 解:轮:平面运动,惯性力系向质心简化厂c三-m MIC=-Ja mg ZF.=0 5,=0T+Fc-mg=0 (分析:此三个方程是何方程的变形) M。=0Mc-Tr=0 [Fic=ma。(无-" 有: Mc=a=mg任 得7 a。=… 「杆a 求A处绳断瞬时: 0 C ⊥A 0处反力 解:杆→转动→惯性力系向转轴简化: ∫Fo=-ma。 Noy MIo=-Joa 绳断瞬时:0=o,∴a=o→即:ae=ad→Fo=F0 ∑Fx=0Nm=0 ΣF,=0Nw+Fo-mg=o >分析此时三个方程的实际意义, M。=0M0-ms30 Fo=ma。=m2a a 有: Mio=Ja= =可得:N 39 3
3 可得: oy ox N N 有: a g P FIC (此时不要有“—”号) 不滑动: F Nf a fg 不翻倒: g h b a b d 2 c a 绳拉力 解:轮:平面运动,惯性力系向质心简化 IC c IC c M J F ma 0 0 0 0 0 M M T r F T F mg F c IC y IC x (分析:此三个方程是何方程的变形) 有: ( “ ” ) 2 ( " " ) 2 (无 号 r mr a M J F ma 无 号 c IC c IC c 得: c a T 杆 O 处反力 解:杆 转动 惯性力系向转轴简化: IO o IO c M J F ma ∵绳断瞬时: o ,∴ a o n c 即: t ac ac t FIO FIO o l M o M mg F o N F mg o F o N o o IO t y oy IO x ox 2 >分析此时三个方程的实际意义, 有: 3 2 2 ml M J l F ma m IO o t c t IO >比较取小者 例: α 判断 求 α 例: 求A处绳断瞬时:
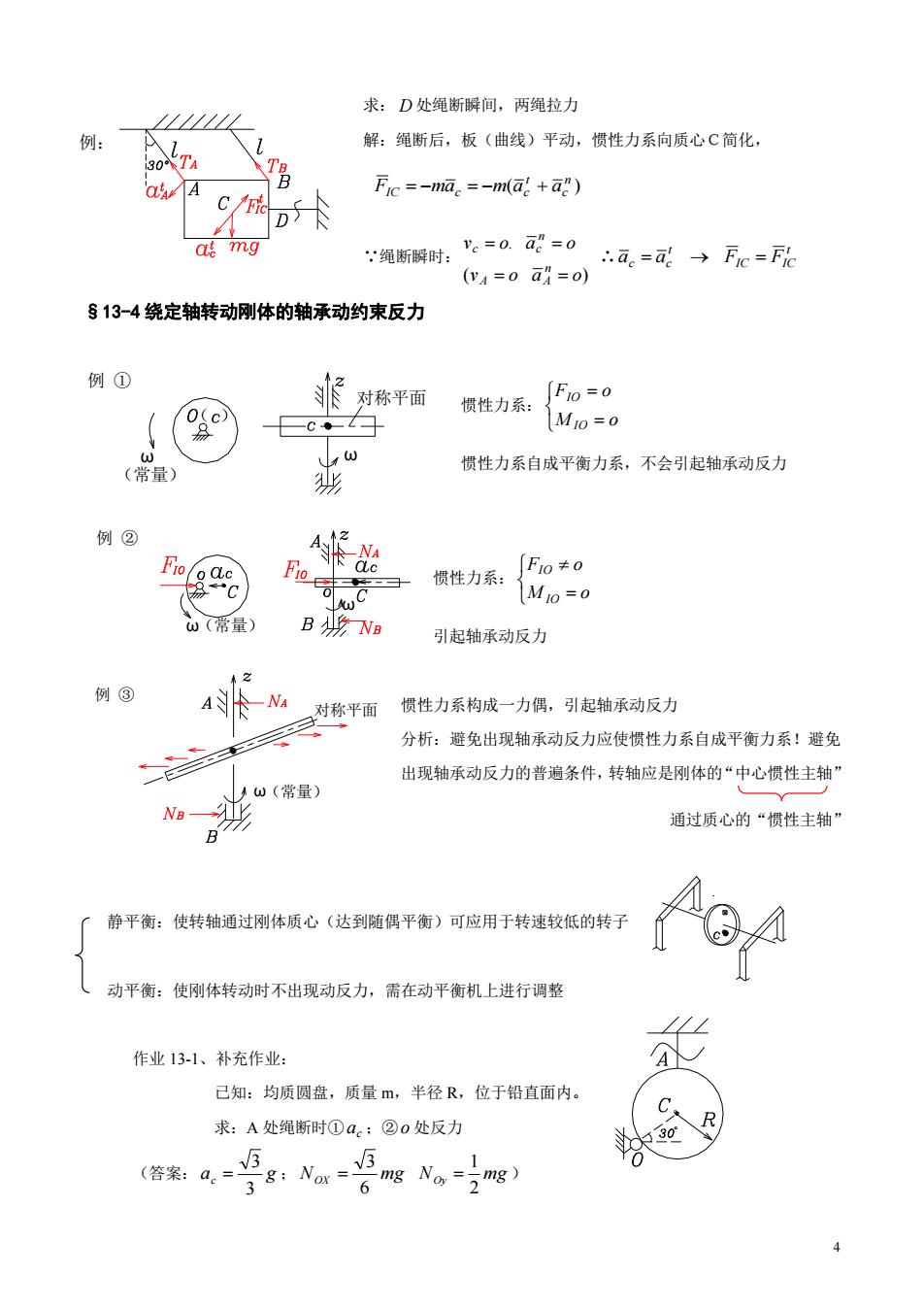
求:D处绳断瞬间,两绳拉力 LZLLt 例: 解:绳断后,板(曲线)平动,惯性力系向质心C简化 Fc=-ma。=-m(a+a) C D 绳断瞬时: =0.a=0a.=d→Fc=F (v4=0a4=o) §13-4绕定轴转动刚体的轴承动约束反力 例① 非对称平面 惯性力系: ∫Fo=o MIo=0 (常量) 惯性力系自成平衡力系,不会引起轴承动反力 例② A内卡& 惯性力系: Fo≠o 1Mo=0 山常量) 引起轴承动反力 2 例③ 惯性力系构成一力偶,引起轴承动反力 分析:避免出现轴承动反力应使惯性力系自成平衡力系!避免 出现轴承动反力的普遍条件,转轴应是刚体的“中心惯性主轴 w(常量) 通过质心的“惯性主轴” 静平衡:使转轴通过刚体质心(达到随偶平衡)可应用于转速较低的转子 动平衡:使刚体转动时不出现动反力,需在动平衡机上进行调整 作业131、补充作业: 己知:均质圆盘,质量m,半径R,位于铅直面内。 求:A处绳断时①a。:②o处反力 30 R
4 ° 求: D 处绳断瞬间,两绳拉力 解:绳断后,板(曲线)平动,惯性力系向质心C简化, ( ) n c t FIC mac m ac a ∵绳断瞬时: ( ) . v o a o v o a o n A A n c c ∴ t IC IC t ac ac F F §13-4 绕定轴转动刚体的轴承动约束反力 惯性力系: M o F o IO IO 惯性力系自成平衡力系,不会引起轴承动反力 惯性力系: M o F o IO IO 引起轴承动反力 惯性力系构成一力偶,引起轴承动反力 分析:避免出现轴承动反力应使惯性力系自成平衡力系!避免 出现轴承动反力的普遍条件,转轴应是刚体的“中心惯性主轴” 通过质心的“惯性主轴” 静平衡:使转轴通过刚体质心(达到随偶平衡)可应用于转速较低的转子 动平衡:使刚体转动时不出现动反力,需在动平衡机上进行调整 作业 13-1、补充作业: 已知:均质圆盘,质量 m,半径 R,位于铅直面内。 求:A 处绳断时① c a ;② o 处反力 (答案: ac g 3 3 ; NOX mg NOy mg 2 1 6 3 ) 例: 对称平面 (常量) ω ω ( ) 例 ① ω 例 ② ω(常量) ω(常量) 对称平面 例 ③