
Chapter3 Reactions(反力) Instructor:Sun,Fei-fei Spet,26th,2014, 同大学 土亦工程学院 11 3.1 reaction forces(反力)for planar structures(平面结构) M (c) 同©大学 土本工相学脱 2
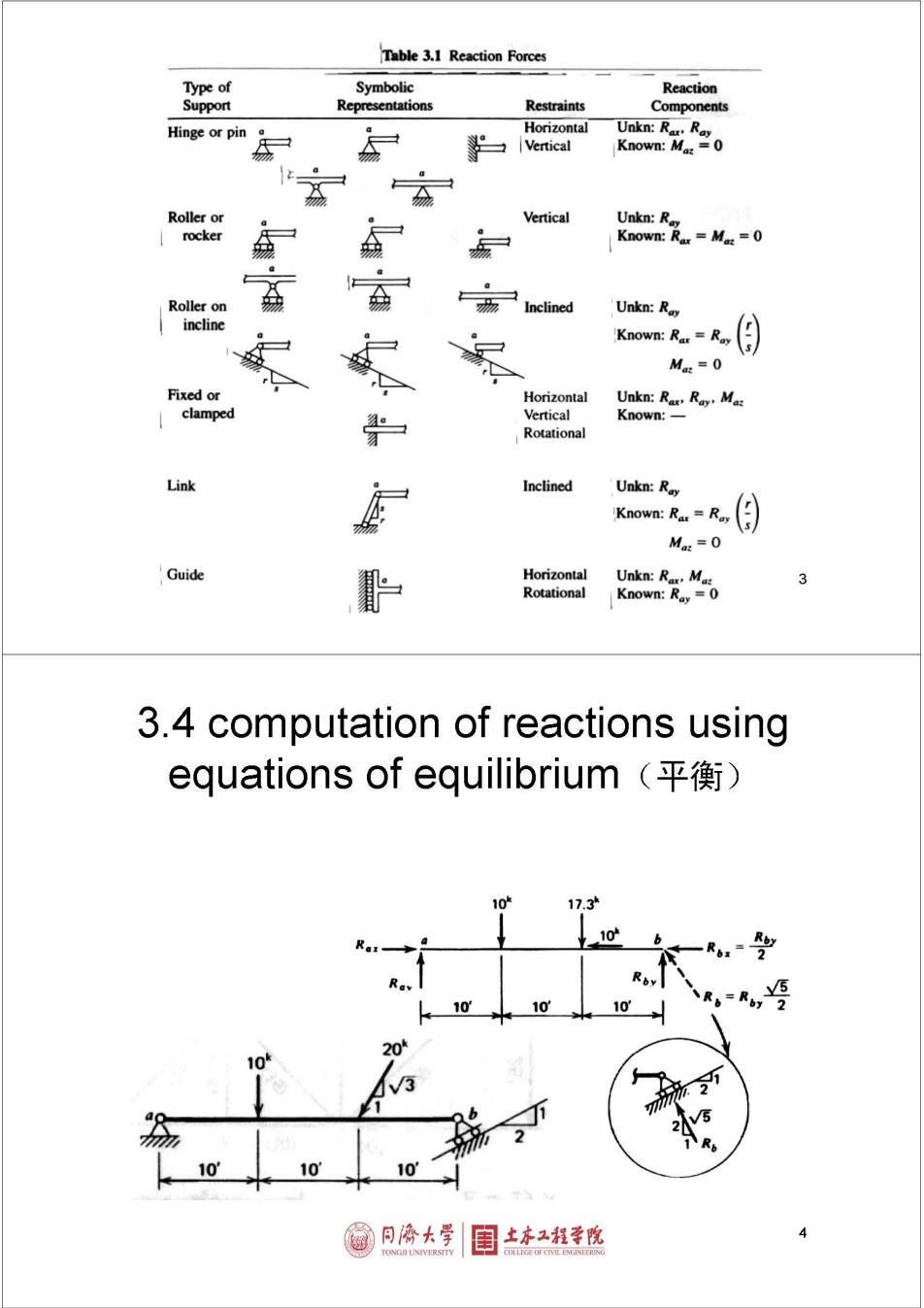
Table 3.1 Reaction Forces Type of Symbolic Reaction Support Representations Restraints Components Hinge or pin Horizontal y Unkn:Rar.Ray Vertical Known:Ma:=0 Roller or Vertical Unkn:Ray rocker Known:Rar Ma:=0 Roller on Inclined Unkn:Ray incline Known:Rar Ray Ma:=0 Fixed or Horizontal Unkn:Rar Ray:Mas clamped Vertical Known:- Rotational Link Inclined Unkn:Ray Known:Rar Ray Ma:=0 Guide 子 Horizontal Unkn:Rar.Ma: Rotational Known:Ray =0 3.4 computation of reactions using equations of equilibrium(平衡) 10 17.3 10 10 10 10 20 10 10 10 同©大学 土亦工程学院

3.5 condition equations for planar structures Indep. React. Numb.of Reg'd.React. Comps. Conditions Comps. Structure ra r=3+n Classification M.=0 4 1 3+1=4 r=r determinate, 6 stable M,=0。 编 12 13+2=5 ra=n determinate. stable 4 3+1=4 ra=r determinate, stable M,=0 15 11 3+1=4 ra>r indeterminate, stable 5 Indep. React. Numb.of Reg'd.React. Comps. Conditions Comps. Structure Ta r=3+n Classification TM=0 5 |2 3+2=5 ru=r. determinate, stable 4 2 3+2=5 r<r unstable M2=0 3 11 3+1=4 ra<r unstable 分 g M2=0:P=00 4 12 3+2=5 ra<r unstable 就 1 同份大子 工水二程子悦

Example Problem 3.4 150kN 120kN Hinge 14 3kN/m A C D 120m 20m Hinge 40m 20m 40m 20m 40m 120kN 90kN RD: 120 kN 3 kN/m 20m 20m 20m 20m 20m 20m 40m Example Problem 3.5 Entire structure 10 10 10 10 20 RB cs For the entire structure: For section BC: ∑M=0)+1020+40+60+80)-540) ∑M=0)+ 1020)+5(20)+Rc(40)-Ro40)=0 (condition equation) -Rg100)-Rc(20)=0 4Rg-4R。=30 Rcr 5Rcy =90 In summary,the equations of equilibrium are ∑P,=0tRw+Rg-4(10)=0 R。+5Rg=90 RA +Rcy=40 RAy +Rc=40 ∑P.=0R-Ro-5=0 Ru -Rcr =5 -4R6+4Rg=30 Ru-R。=5 同桥大学 土床工程学院
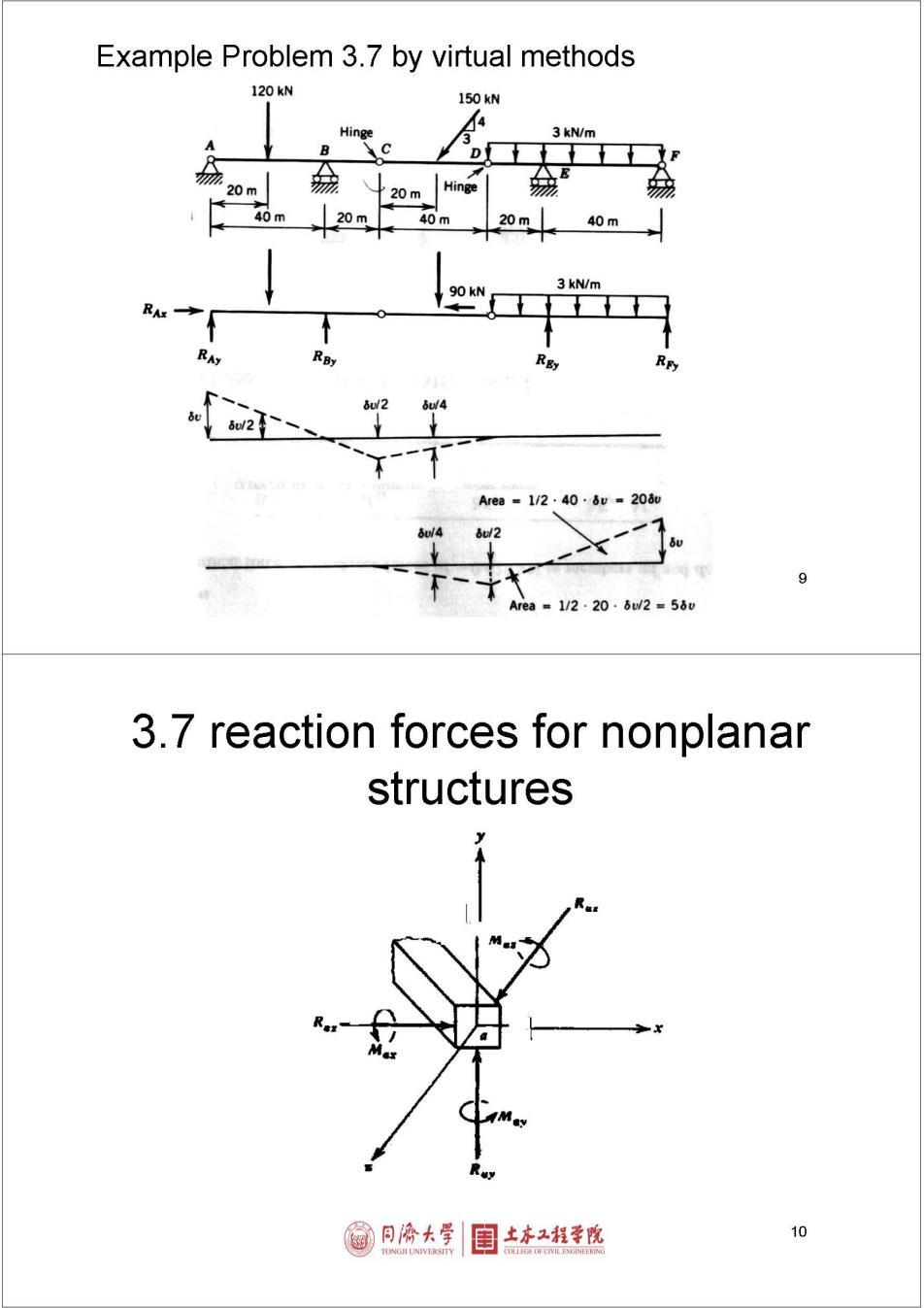
Example Problem 3.7 by virtual methods 120kN 150kN 4 Hinge 3 kN/m B 20m 20m Hinge 40m 20m 40m 20m 40m 90 kN 3 kN/m RF Area=1/2.40·6u=20加 9 Area=1/2·20.6uW2=56v 3.7 reaction forces for nonplanar structures 园何海大学 土本2程学院 10

Symbolic Representation Restraints Reaction Components Type of Transla- Rota- Support Plan" Elevation" tional tional Known Unknown Fixed 家 x%2 xX z Nothing Rar:Ray Raz:Mat May:Mat Sleeve 名yz Mez =0 Rar Ray (pinned Raz Mar about Mey -●wiel Universa 名男2 Ma=Mg Rat Ray joint Ra Roller (free 1%2 Rar=0 Ray:Rat to roll in Mar=Moy x direction =M=0 Rar=Roz=0 Ball Mar=May =Ma=0 @同海大学 土亦工程学院 11 3.8 external static determinacy(静定) and stability for nonplanar structures ·Ra6:statically indeterminate(超静定) externally(necessary but not sufficient) 同©大学 土亦工程学院 12
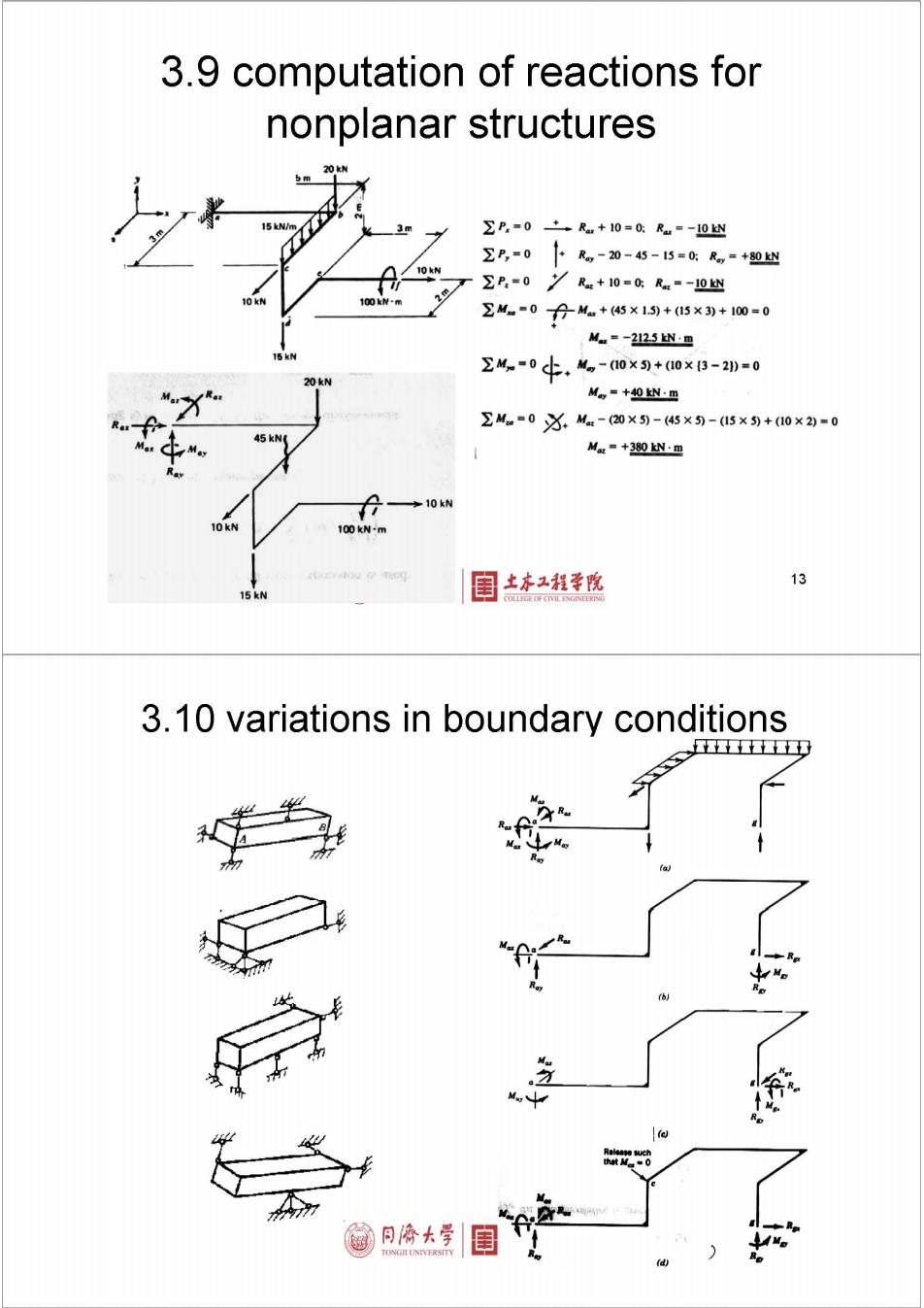
3.9 computation of reactions for nonplanar structures m ∑P,=0+R+10=0:R=-0y ∑P,=0 卜R,-20-45-15=0GR,=+0四 ∑B,=0丫Re+10=cRe=-10四 100kN-m ∑M-0合M+45×1+5×3)+100=0 M=-225W:m ∑M。-0十.M,-0×+a0×B-20=0 M =+40 kN:m ∑M。=0X.Ma-(20×)-45×)-5×)+(0×2)-0 45 kN M=+380y:四 →10kN 10 kN 100kN-m 土本工程学院 13 3.10 variations in boundary conditions 四 同溶大号