
(22) §12-6普通定理的综合应用举例.(§12-4、§12-5不要求) 动量定理 >矢量形式(解题时应用投影式) 动力学普通定理 动量矩定理 动能定理 一标量形式 「☆可用不同定理求解同一问题 分类 、☆须综合应用不同定理求解 例: 厂1、a 求:2、A轮绳拉力及地面反力 (3、B.处反力 (注:一般可首选动能定理) 1、整体:,应用动能定理T2-T=∑w了=0(注意:受力及运动分析) mvmmg +2m) 工w=%g。即:Cm+ma+2m,)=m,助: 求导:2y4·a4()=megvc 有:e=2y4→∴可得a4=… 2、轮A:应用平面运动微分方程 xma4=T,”-F T A y:0=N-mg →得{ o:Ja4’=T4R+FR F IN? 有a=% 3、轮B ①油定轴转动微分方程(Ja=∑m(E) Jaaa=Tc·Ra-TRa→得:Tc= TN品qe 有a=20,(他可分标物c得。= 令由质心运动定理 mag x:mgag =N-Ti =.. (重点:动能定理 平面运动微分方程
1 动力学普通定理 分类 §12-6 普通定理的综合应用举例.(§12-4、§12-5 不要求) 动量定理 动量矩定理 动能定理 — 标量形式 ☆.可用不同定理求解同一问题 ☆.须综合应用不同定理求解 1、 A a 求: 2、A轮绳拉力及地面反力 3、B.处反力 (注:一般可首选动能定理). 1、整体:.应用动能定理 T2 T1 w T1 o (注意:受力及运动分析) 2 ) 4 3 ( 2 1 2 1 2 1 2 1 2 2 2 2 2 2 A A A A B B c c A mA mB mc T m v J J m v v w mcghc 即: A mA mB mc mc ghc v 2 ) 4 3 ( 2 求导: A aA mc gvc 2v () ∵有: c A v 2v . ∴:可得 aA 2、轮A: 应用平面运动微分方程. A A A A A A A A A A A A J T R F R y o N m g x m a T F ? ? ? ? : : : 得 A A A F N T 有: A A A R a 3、轮B ①由定轴转动微分方程( ( ) e z mz Fi J ) B B TC RB TA RB J 得: TC 有: B A B R 2a (也可分析物 C 得 TC ) ②.由质心运动定理. By B C o B By Bx A o B Bx y m a N m g T x m a N T : : 得 By Bx N N (重点: >矢量形式(解题时应用投影式) 纯滚动 例: ω ω α α (22) 动能定理 平面运动微分方程

已知:A、B两轮质量均为m,对转轴转动惯量均为J,C物质量为m。 初始系统静止且弹簧为原长。 l、ye、ae c 求:物C下降h。时的 2、齿轮间的(切向)啮合力 3、B处反力 解:1、整体:应用T2-T=∑wT=0 似+0+0 工w=风g成-=观欧哈是灵孕=风碱一克 对风+的=风晚竞妮户备 求导2。a.()=m8-22得:a:= Te 2、c物: meg-T。=mea。→得:Te=… a 3、B轮 F Fr 哈合力:鑫向 E:切向 有:F,=F,g0(0:压力角,一般己知) O应用定轴转动微分方程:Js4s=了R-E·2→F=…→可得:F,及F ②应用质心运动定理 即: x:mgd ge=∑F→0=Nm+F,→N=… y:mg4=∑F→0=N-E-mBg-T。=0→N=… (简单说明教材中的解法,将B轮与C物一起分析,利用质点系的动量和动量矩定理。学生自习) 2
2 已知:A、B两轮质量均为 m ,对转轴转动惯量均为 J ,C 物质量为 mc 初始系统静止且弹簧为原长。 1、 c v 、 ac 求:物 C 下降 c h 时的 2、齿轮间的(切向)啮合力 3、B处反力 解:1、整体:应用 T2 T1 w T1 0 2 2 2 2 2 2 2 ) 1 2 ( 2 1 ( ) 2 1 2 1 2 1 2 1 2 1 R R R v J R v T m v J J m v J c c c c B B A A c c ) 8 5 2 1 ) ( 4 5 ( 2 1 2 2 2 2 R J v m R J vc mc c c 2 2 2 32 ) 2 1 2 ( 2 1 2 1 c c c c c c c c h k m gh R R R R h W m g h k s m gh k 即: 2 2 2 32 ) 8 5 2 1 ( c c c c hc k m gh R J v m 得: vc 求导: c c c c hc vc k v a m g v 2 32 2 () 得: ac mc g Tc mcac 得: Tc 3、B轮 啮合力 F 切向 F :径向 t r : 有: F r Ft tg (θ :压力角,一般已知) ①应用定轴转动微分方程: B B c t Ft R J T R F 2 可得: Fr 及 F ②应用质心运动定理 即: By t B c By e B Bx x Bx r Bx e B Bx x y m a F N F m g T N x m a F N F N : 0 0 : 0 (简单说明教材中的解法,将 B 轮与 C 物一起分析,利用质点系的动量和动量矩定理。学生自习) ω 例: ω α (24) 2、 物: θ
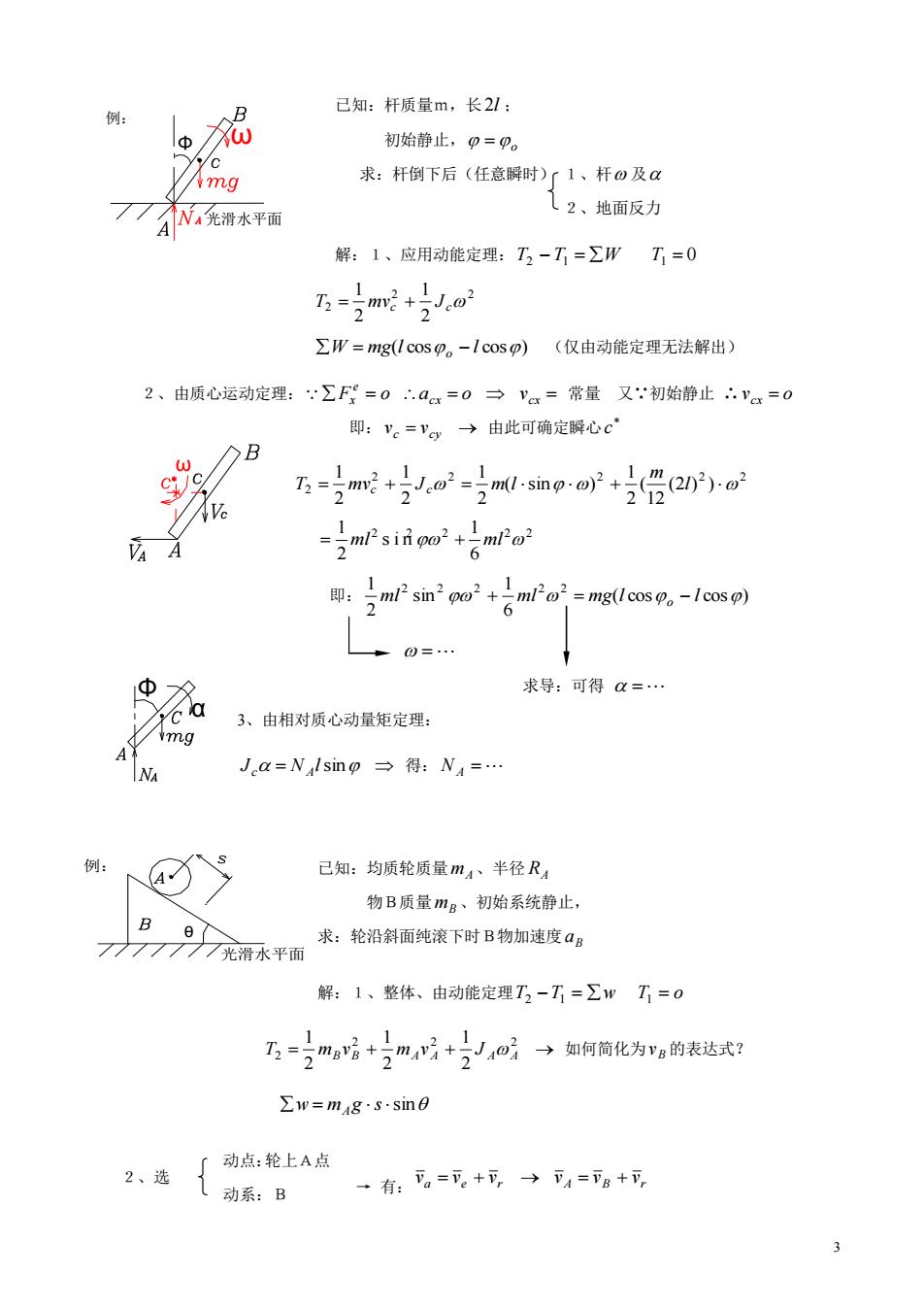
例: R 已知:杆质量m,长21: 初始静止,p=p。 求:杆倒下后(任意瞬时)1、杆o及 77:流水平面 12、地面反力 解:1、应用动能定理:T3-7=∑WT1=0 =m2+J,o2 ∑W=mg(1cosp。-1cosp)(仅由动能定理无法解出) 2、由质心运动定理:∑F=0aa=0→va=常量又:初始静止∴vx=0 即:V。=vg→由此可确定瞬心c 万-m+o-smpo+20)-o 1 房A 0=… 中 求导:可得a=… 3、由相对质心动量矩定理: Jea=N Isino→得:N4=… 例: 已知:均质轮质量m半径R4 物B质量mg、初始系统静止, B 求:轮沿斜面纯滚下时B物加速度ag 7光滑水平面 解:1、整体、由动能定理T2-T=∑wT=o 乃=2m哈+与m听+4o→如何简化为vg的表达式? w=mg·s:sin0 法{ 一有:可,=元。+元,→4=下g+可
3 2、选 已知:杆质量m,长 2l ; 初始静止, o 求:杆倒下后(任意瞬时) 1、杆 及 2、地面反力 解:1、应用动能定理: T2 T1 W T1 0 2 2 2 2 1 2 1 T mvc Jc W mg(l cos l cos) o (仅由动能定理无法解出) 2、由质心运动定理: F o e x acx o vcx 常量 又∵初始静止 ∴ vcx o 即: vc vcy 由此可确定瞬心 c 2 2 2 2 2 2 (2 ) ) 12 ( 2 1 ( sin ) 2 1 2 1 2 1 l m T mv J m l c c 2 2 2 2 2 6 1 sin 2 1 ml ml 即: ( cos cos ) 6 1 sin 2 1 2 2 2 2 2 ml ml mg l o l 求导:可得 3、由相对质心动量矩定理: Jc NA lsin 得: NA 已知:均质轮质量 mA 、半径 RA 物B质量 mB 、初始系统静止, 求:轮沿斜面纯滚下时B物加速度 B a 解:1、整体、由动能定理 T2 T1 w T1 o 2 2 2 2 2 1 2 1 2 1 B B A A A A T m v m v J 如何简化为 B v 的表达式? w mA g ssin 动点:轮上A点 动系:B Φ ω 光滑水平面 例: ω α Φ 光滑水平面 例: θ → 有: a e r A B r v v v v v v
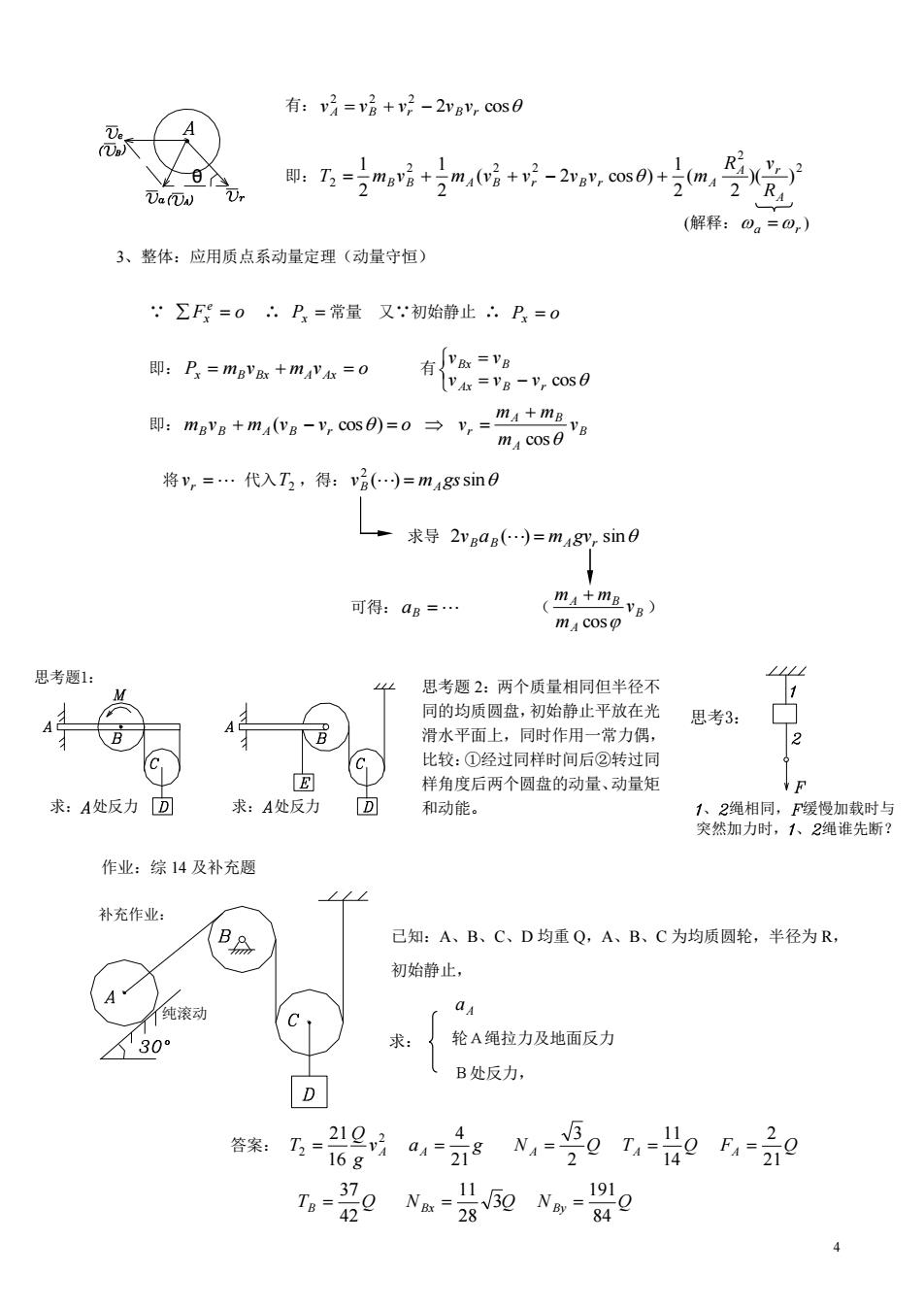
有:v7=层+2-2vBy,cos0 Ta⑦W 5-gng+成-%w+mg觉 (解释:0。=0,) 3、整体:应用质点系动量定理(动量守恒) :∑F=0.P=常量又:初始静止.P=0 即:P=mgV+mAV=0 有a= vu=g-y,cos日 即:mvg+m,a-,cs=0今,=m4+m 将y,=…代入T,得:v()=mags sin8 求导2y0)=m8,s血0 可得:ag=… 品 思考题1: 思考题2:两个质量相同但半径不 同的均质圆盘,初始静止平放在光 思考3: 滑水平面上,同时作用一常力偶, 2 G 比较:①经过同样时间后②转过同 样角度后两个圆盘的动量、动量矩 求:A处反力回 求:A处反力 和动能。 大、2绳相同,F缓慢加载时与 突然加力时,1、2绳谁先断 作业:综14及补充题 L∠ 补充作业: B 已知:A、B、C、D均重Q,A、B、C为均质圆轮,半径为R 初始静止, 纯滚动 30 轮A绳拉力及地面反力 B处反力, D 5器0,京90060 4 37
4 纯滚动 补充作业: 求: 求: 处反力 求: 处反力 思考题1: 思考题 2:两个质量相同但半径不 同的均质圆盘,初始静止平放在光 滑水平面上,同时作用一常力偶, 比较:①经过同样时间后②转过同 样角度后两个圆盘的动量、动量矩 和动能。 、 绳相同, 缓慢加载时与 突然加力时, 、 绳谁先断? 思考3: 有: 2 cos 2 2 2 A B r B r v v v v v 即: 2 2 2 2 2 2 )( ) 2 ( 2 1 ( 2 cos ) 2 1 2 1 A A r B B A B r B r A R R v T m v m v v v v m (解释: a r ) 3、整体:应用质点系动量定理(动量守恒) ∵ F o e x ∴ Px 常量 又∵初始静止 ∴ Px o 即: Px mB vBx mA vAx o 有 Ax B r cos Bx B v v v v v 即: mB vB mA (vB vr cos) o B A A B r v m m m v cos 将 vr 代入 T2 ,得: ( ) sin 2 v m gs B A 求导 2vBaB () mA gvr sin 可得: aB ( B A A B v m m m cos ) 作业:综 14 及补充题 已知:A、B、C、D 均重 Q,A、B、C 为均质圆轮,半径为 R, 初始静止, A a 轮A绳拉力及地面反力 B处反力, 答案: 2 2 16 21 A v g Q T aA g 21 4 NA Q 2 3 TA Q 14 11 FA Q 21 2 TB Q 42 37 NBx 3Q 28 11 NBy Q 84 191 θ