
第八章刚体的平面运动 (14) 例 (曲柄0A:转动 0 B A轮:运动形式? (连杆AB:运动形式? §8-1刚体平面运动的概述和运动分解 平面运动:运动中,刚体上任一点与某固定平面的距离始终不变 A (即:刚体上各点都在平行于某固定平面的平面内运动 设:刚体相对固定平面1作平面运动 用平面Ⅱ(ⅡI)截得平面图形S→S始终在Ⅱ平面内运动 取直线AA2与I面垂直→A42平动→AA2上各点可由S上A点代表 即:刚体上所有各点都可用S面上相应的点来代表 结论:刚体的平面运动可以简化为平面圆形在其自身平面内的运动。 平面图形位置的确定 x。=(0) S 任取一线段0'My。=f() “平面运动方程”(三个自由度) p=f50 「☆若:=常量,则:刚体平移 分析 x。=常量 ☆若: 侧:刚体转动 y。=常量 即:平面运动分解平动 1转动 (但注意:平动十转动≠平面运动) 例1 ,直线行驶轮的平面运动 分解了随车平动:“牵连运动” L相对0转动:“相对运动” 2 当单独轮运动时,可建立一平动参考系oxy
1 ☆若: 常量,则:刚体平移 ☆若: y 常量 x 常量 o o ,则:刚体转动 分析 平动 转动 第八章 刚体的平面运动 §8-1 刚体平面运动的概述和运动分解 平面运动:运动中,刚体上任一点与某固定平面的距离始终不变。 (即:刚体上各点都在平行于某固定平面的平面内运动) 设:刚体相对固定平面Ⅰ作平面运动 用平面Ⅱ(Ⅱ∥Ⅰ)截得平面图形 S S 始终在Ⅱ平面内运动 取直线 A1A2 与Ⅰ面垂直 A1A2 平动 A1A2 上各点可由 S 上 A 点代表 即:刚体上所有各点都可用 S 面上相应的点来代表. 结论:刚体的平面运动可以简化为平面圆形在其自身平面内的运动。 平面图形位置的确定 即:平面运动分解 (但注意:平动+转动 ≠ 平面运动) 轮的平面运动 当单独轮运动时, 可建立一平动参考系 o x y ω 例 曲柄 :转动 滑块 :平动 连杆 :运动形式? 轮:运动形式? ω Ⅱ Ⅰ 固定平面 φ 直线行驶 例 任取一线段 ( ) ( ) ( ) 3 2 1 f t y f t x f t O M o o “平面运动方程” (三个自由度) (14) 随 车 平 动:“牵连运动” 相对 O 转动:“相对运动” 分解

yy 般情况:可任取一点0'建立一平动参考系0xy'(注:x'、y的方向始终不变) 0':基点(注:平动参考系并未与刚体固连,可想象为销钉连接) 平面运动分解防基点平动十绕基点转动 (绝对) (牵连)+(相对) (注:三种运动均为刚体的运动,与点的合成运动的概念稍有不同) 「☆、随基点平动的速度,加速度与基点的选取有关 注:基点可以任意选取,但☆、绕基点转动的角速度,角加速度与基点的选取无关 AB杆:平面运动 在时间△t内,从水平位置AB→AB位置 ①选取点A为基点,AB平面运动厂 随基点A(曲线)平动 AB'B 绕基点A转动 ②选取点B为基点,AB平面运动厂基点B(值线)平动 儿绕基点B转动 B→ s8-2求平面图形内各点速度的基点法 选基点0 M。 M 00 已知:某解时 随基点0'平动 绕基点0'转动 求:下 下。:牵连速度 下:相对速度(有:=6O) 即:下y=g+下M0“基点法”(平面矢量方程,可求解两个未知量) 结论:平面图形上任一点的速度等于基点的速度与该点绕基点转动速度的矢量和。(亦称“合成法”) 例乙Ua4 已知:4:求: OAB 解:1、确定研究对象选取基点:AB杆:基点:A(通常选取运动已知的点) D i 2、速度分析一速度图 、应用基点法公式求解、多别 (va=vactgo 可得 (思考:若求下)
2 Δφ 分解 ω 选基点 o ω 随基点 o 平动 o v :牵连速度 + 绕基点 o 转动 Mo v :相对速度(有: vMo Mo ) 已知:某瞬时 o v 求: vM 已知: A v ;求: AB B v 可得 sin lsin v AB v v v v v ctg BA A AB A BA B A (思考:若求 D v ) 3、应用基点法公式求解、 ? A BA ? B v v v 一般情况:可任取一点 o 建立一平动参考系 o x y (注: x 、 y 的方向始终不变) o :基点(注:平动参考系并未与刚体固连,可想象为销钉连接) 平面运动 随基点平动 + 绕基点转动 (绝对) (牵连) + (相对) (注:三种运动均为刚体的运动,与点的合成运动的概念稍有不同) 注:基点可以任意选取,但 AB 杆:平面运动 在时间Δ t 内,从水平位置 AB AB 位置 随基点 A(曲线)平动 绕基点 A 转动 随基点 B(直线)平动 绕基点 B 转动 §8-2 求平面图形内各点速度的基点法 即: M O MO v v v “基点法”(平面矢量方程,可求解两个未知量) 结论:平面图形上任一点的速度等于基点的速度与该点绕基点转动速度的矢量和。(亦称“合成法”) 解:1、确定研究对象选取基点:AB 杆;基点:A(通常选取运动已知的点) 2.、速度分析 → 速度图 φ 例 φ φ 例 ω ☆、随基点平动的速度,加速度与基点的选取有关 ☆、绕基点转动的角速度,角加速度与基点的选取无关 ①选取点 A 为基点,AB 平面运动 ②选取点 B 为基点,AB 平面运动

基点法公式:下B=下4+下B 投影式何。B=)4B+区丛:(何,)B=,m“速度投影定理 结论:同平面图形上任意两点的速度在此两点连线上的投影相等。 进人文龙用于已纯两点速度方向且知其一在速度大小一 p 已知:OA之w 求:图示位置时vE 1.AB:Va Cos30°=v →得vB 309 A 解: 2.CD:)DC →得vo 60 3.E:VE COS30°=yo →得yE §8-3求平面图形内各点速度的瞬心法 1、速度瞬心的概念(定理) W 求:下,垂线AN上各点速度 UCA- 基点:A,则有:可e=下4+4→=VA-VA (=CA.@) 若有:CA-" 则:Ve=V4-ve4=0 结论:一般每一瞬时,平面图形上(或其延伸部分)都唯一地存在一个速度为零的点 -VA C:“瞬时速度中心”→简“速度瞬心”(或“瞬心”) 2、速度分布与瞬心的关系 若:已知瞬心C及山 A 则:选基点:瞬心C一有,=。+k=。一 y4=AC·o垂直AC B 下B=下 VB=BC·O垂直BC 绕“瞬时速度中心”的瞬时转动 又称“瞬时转动中心” 〔①不同瞬时,瞬心为不同的点 注意 ②瞬心速度为零,加速度不一定为
3 投影式 0 ( ) ( ) ( ) B AB A AB BA AB v v v : B AB A AB (v ) (v ) “速度投影定理” 若有: A v CA 则: vc vA vcA 0 基点法公式: B A BA v v v 结论:同平面图形上任意两点的速度在此两点连线上的投影相等。 ☆常用于已知两点速度方向,且知其一点速度大小时 ☆无法解出ω 已知:OA 之ω 求:图示位置时 E v 解: §8-3 求平面图形内各点速度的瞬心法 1、速度瞬心的概念(定理) 求: A v 垂线 AN 上各点速度 基点:A,则有: c A cA c A cA v v v v v v (v CA) cA 结论:一般每一瞬时,平面图形上(或其延伸部分)都唯一地存在一个速度为零的点。 C:“瞬时速度中心” 简“速度瞬心”(或“瞬心”) 2、速度分布与瞬心的关系 若:已知瞬心 C 及ω 绕“瞬时速度中心”的瞬时转动 又称“瞬时转动中心” ①不同瞬时,瞬心为不同的点。 ②瞬心速度为零,加速度不一定为零 ω 例 ω ω ω 注 E D E D B D B A B 、E: v v v DC v BC v 、CD: v 、AB: v v v 得 得 得 3. cos30 2 ( ) 1 cos30 则:选基点:瞬心 C → 有 B Bc A c Ac Ac v v v v v v v BC BC v AC AC B A 垂直 垂直 注意
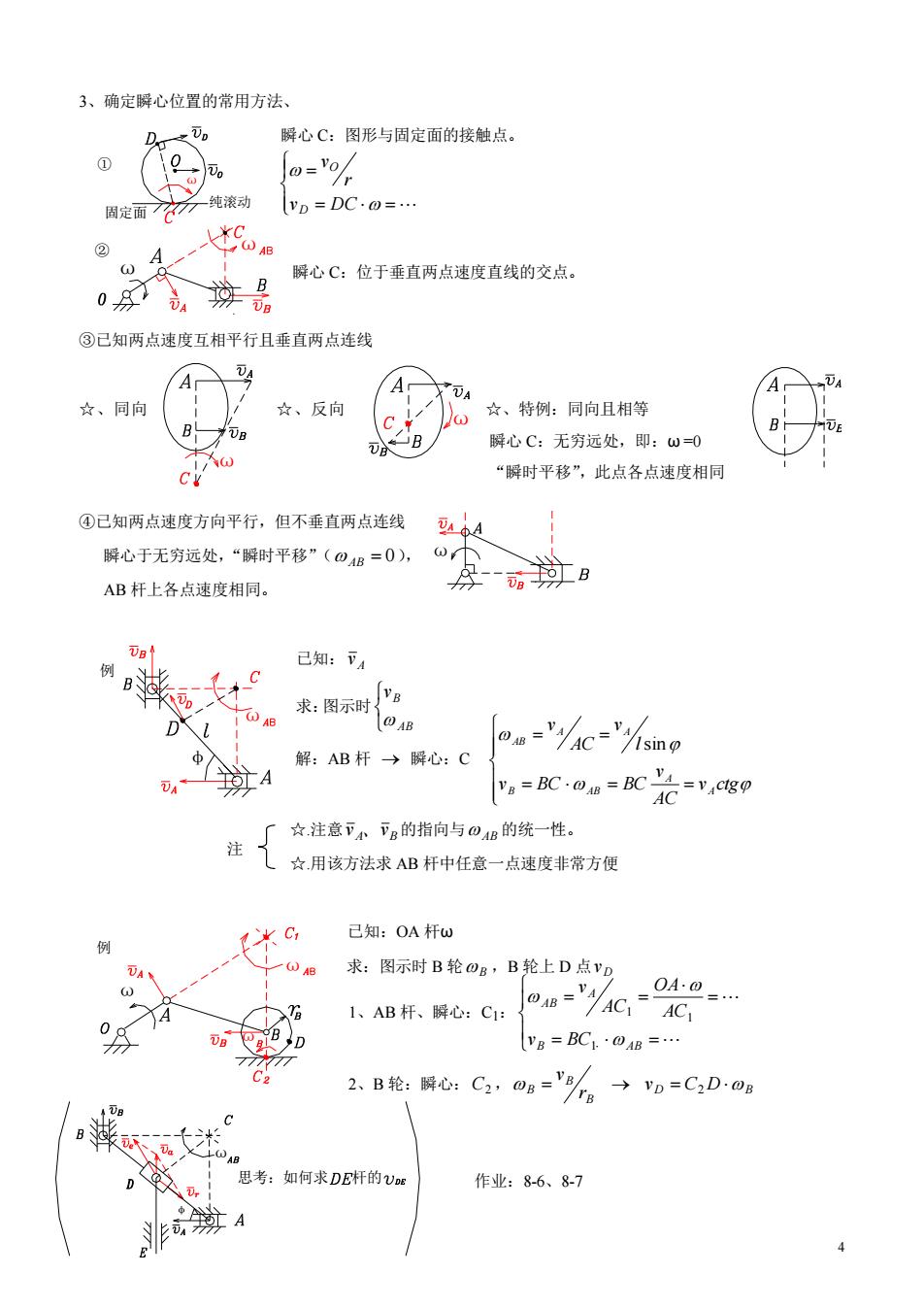
3、确定瞬心位置的常用方法、 瞬心C:图形与周定面的接触点。 o= 周定面7 一纯滚动 VD =DC.0= 瞬心C:位于垂直两点速度直线的交点。 ③已知两点速度互相平行且垂直两点连线 ⑦ A ☆、同向 ☆、反向 ☆、特例:同向且相等 ⑦g B 解心C:无穷远处,即:w=0 c “瞬时平移”,此点各点速度相同 ④己知两点速度方向平行,但不垂直两点连线 瞬心于无穷远处,“瞬时平移”(0相=0), AB杆上各点速度相同。 已知:下 A 求:图示时 C=/sing 解:AB杆→瞬心:C =cou=ct=,限e ☆注意下下g的指向与04B的统一性。 注 ☆.用该方法求AB杆中任意一点速度非常方便 已知:OA杆w 求:图示时B轮Og,B轮上D点VD 1、AB杆、瞬心:C1: Vg=BC·OAB= 2B轮:明:C0='。→n=CD0 思考:如何求DE杆的va 作业:8-6、87
4 ω 瞬心 C:无穷远处,即:ω =0 “瞬时平移”,此点各点速度相同 v DC r v D O 解:AB 杆 瞬心:C v ctg AC v v BC BC l v AC v A A B AB A A AB sin 求:图示时 AB B v 1、AB 杆、瞬心:C1: B AB A AB v BC AC OA AC v 1 1 1 2、B 轮:瞬心: C2 , D B B B B v C D r v 2 3、确定瞬心位置的常用方法、 瞬心 C:图形与固定面的接触点。 瞬心 C:位于垂直两点速度直线的交点。 ③已知两点速度互相平行且垂直两点连线 ☆、同向 ☆、反向 ☆、特例:同向且相等 ④已知两点速度方向平行,但不垂直两点连线 瞬心于无穷远处,“瞬时平移”( AB 0 ), AB 杆上各点速度相同。 已知: A v ☆.注意 A B v 、 v 的指向与 AB 的统一性。 ☆.用该方法求 AB 杆中任意一点速度非常方便 已知:OA 杆ω 求:图示时 B 轮 B ,B 轮上 D 点 D v 作业:8-6、8-7 ω ① 纯滚动 固定面 ω ω ② ω ω φ ω 例 ω ω ω 例 φ ω 思考:如何求 杆的 注