
Structural Dynamics Lecture 5: Response to Arbitrary,Step and Pulse Excitations 目 19 同桥大学 本之程学成
Structural Dynamics Lecture 5: Response to Arbitrary, Step , and Pulse Excitations

Contents Response of SDOF to arbitrary excitation ·Duhamel's integral Response to Special Force Types ·Step Force Ramp or Linearly Increasing Force ·Step Force ·Impulsive Force 目 土本鞋李悦
Contents Response of SDOF to arbitrary excitation • Duhamel’s integral Response to Special Force Types • Step Force • Ramp or Linearly Increasing Force • Step Force • Impulsive Force
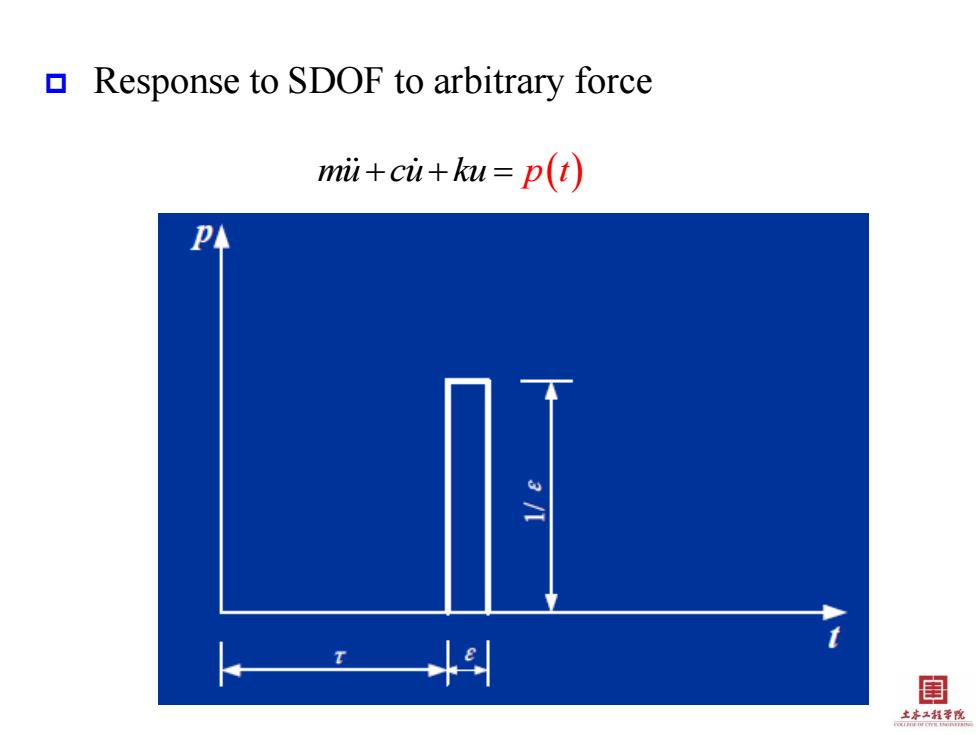
Response to SDOF to arbitrary force mii+cu+ku=p(t) PA 目 土茅红指等院
Response to SDOF to arbitrary force mu cu ku p t

▣Duhamel's integral mii+cu+ku=p(t) u(t)=p()h(i-z)dz 。 Duhamel's integral(convolution integral or superposition integral)is a well-known approach to the solution of transient (or arbitrary load)vibration problems in linear systems.Its development is based on the superposition of the response of the system to a sequence of impulse. Response to unit impulse Unit impulse-response function h-)=2sn[a,t-】1≥r m0, -小.-l12 目 土本程李悦
Duhamel’s integral • Duhamel’s integral (convolution integral or superposition integral) is a well-known approach to the solution of transient (or arbitrary load) vibration problems in linear systems. Its development is based on the superposition of the response of the system to a sequence of impulse. Response to unit impulse • Unit impulse-response function 0 t mu cu ku u p t d p t t h 1 sin n t D D h t e t t m 1 sin n n h t t t m
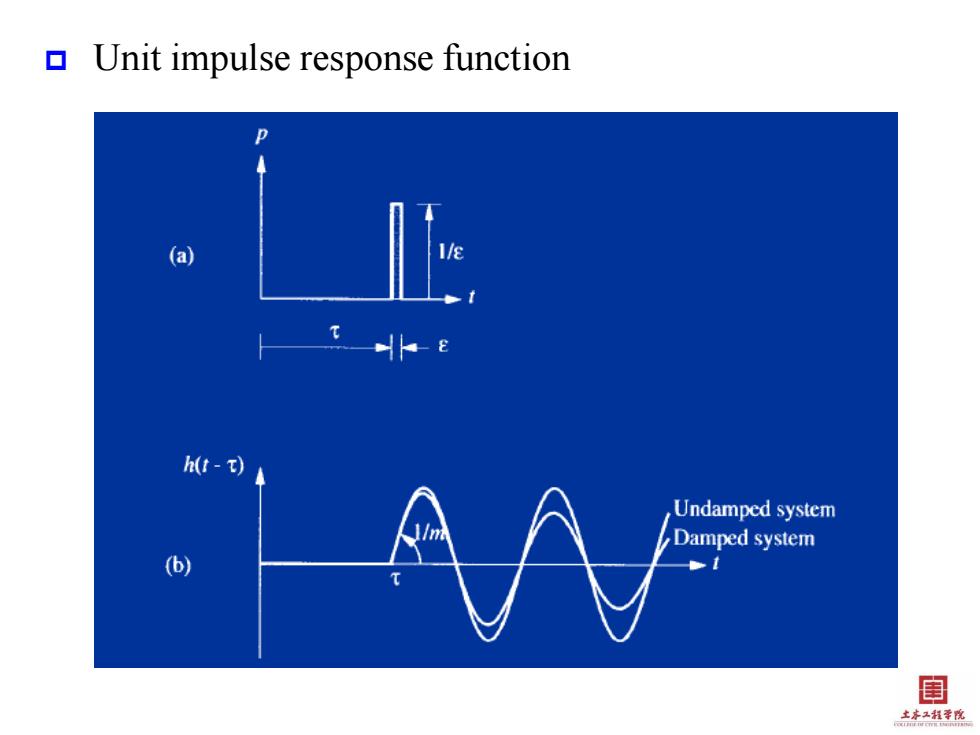
Unit impulse response function (a) h(t-t) Undamped system Damped system b)》 目 土李红程季悦
Unit impulse response function
Response to arbitrary force 12 闺 土本程李悦
Response to arbitrary force

Response of SDOF to special excitation Step force Ramp or linearly increasing force Step force with finite rise time ·Impulsive Force Response of SDOF to pulse excitation Rectangular pulse ·Half cycle sine pulse Triangular pulse force 目 主京2相季院
Response of SDOF to special excitation • Step force • Ramp or linearly increasing force • Step force with finite rise time • Impulsive Force Response of SDOF to pulse excitation • Rectangular pulse • Half cycle sine pulse • Triangular pulse force
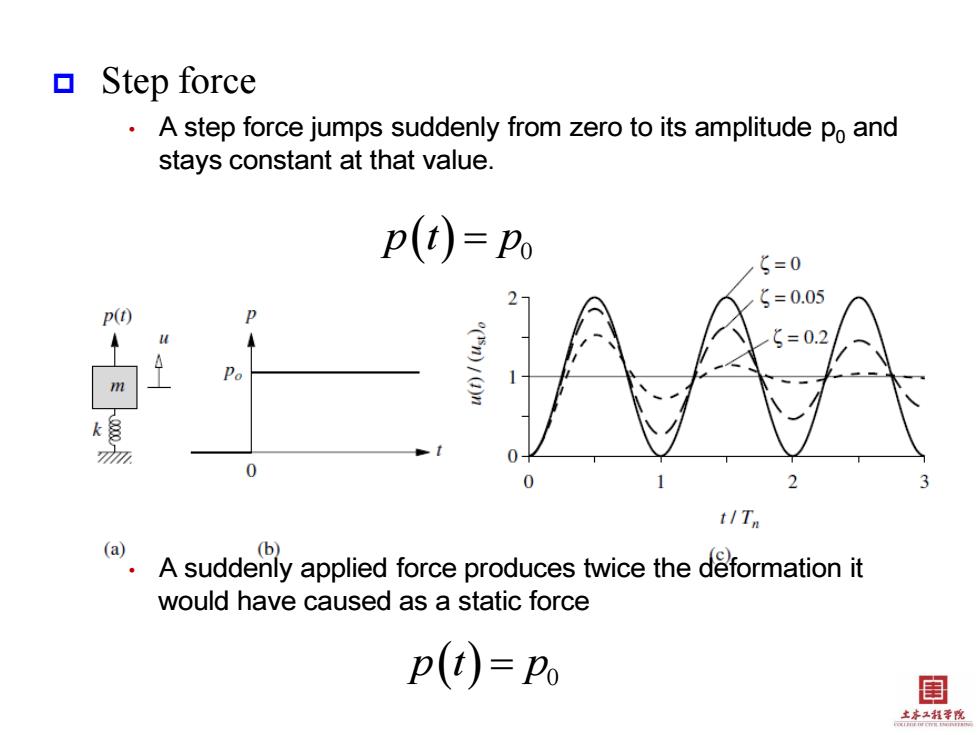
Step force A step force jumps suddenly from zero to its amplitude po and stays constant at that value. p(t)=Po 5=0 g=0.05 p() =0.2 0 0 t/Tn (a) (b) A suddenly applied force produces twice the deformation it would have caused as a static force P(i)=Po 闺 土本程李悦
Step force • A step force jumps suddenly from zero to its amplitude p0 and stays constant at that value. • A suddenly applied force produces twice the deformation it would have caused as a static force 0 p t p 0 p t p

Response of SDOF to step force ·Non-damping case u(0=朵(1-cos04) Under-damped case a-aw产m个 A suddenly applied force produces twice the deformation it would have caused as a static force max(u(o)=22=2(u,)。 k 目 土本2程学院
Response of SDOF to step force • Non-damping case • Under-damped case A suddenly applied force produces twice the deformation it would have caused as a static force 0 1 cos n p u t t k 0 2 1 cos sin 1 n t D D P u t e t t k 0 max 2 2 st 0 p u t u k
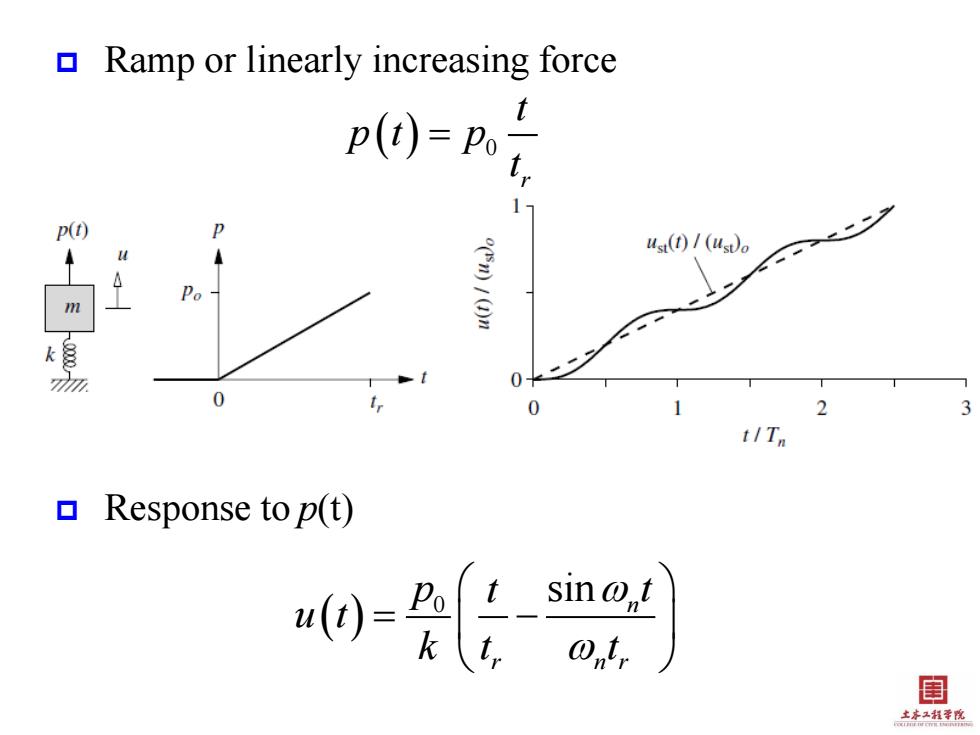
Ramp or linearly increasing force p(t)=P t 1 P(t) us(t)1 (uso L4 Po (n)1(1)n 0 0 0 3 t/Tn ▣Response to p(t) 闺 土本程李悦
Ramp or linearly increasing force Response to p(t) 0 r t p t p t 0 sin n r n r p t t u t k t t