
Chapter 7 Elastic Deflections(弹) of Trusses and Frameworks. B B' F2 F F3 C A 月济大学 土工程学院 TONGI UNIVERSITY COLLEGE OF CVIL ENGINEERING 7.1 description of truss deflection () problem Deformation of members -> deflections of trusses Reasons for determining deflections: >Serviceability requirements() >The analysis process of statically indeterminate structures Type of deformation: when the loads are removed, >Elasticity (弹性) recoverable >Plasticity(性) permanent or nonrecoverable in nature 月大学 土工程学院 2 TONGJI UNIVERSITY OGIRG

7.2 axial force(轴力)-deformation(变形) relationships Area dl F =Ee E= 0= dx A a dl dx EA 子 dl= Fl EA →F= E队 Jo EA A=foF F=kaA fa= EA EA ka= 卡2程学院 3 Elastic Inelastic Elastic Inelastic 7.3 truss deflections by complementary virtual work -unit load method P System:Virtual force system in equilibrium. D System:Actual deformation pattern that is geometrically compatible. d故 dLo=EA (a) 豆amn-2(e 极☐→ 色PSystem 6) 含w-(ar,2 D System “ 2aPD,=2i小Mol

7.4 application of complementary virtual work method 50 0.5 P System 1 50 0.5 62.5 225 Fo ber forces in kN 0.625 5Fp bar forces in kN 1 150 200 0.5 187.5 250 0.625 0 0 504 200 0.5 a 75 6 D System 150 0.6670 P System 2 0.667 0.500 0.834 8 Fp bar forces in kN 品 c P6, .0 0.834 0.667 同海大 TONGI UNIVE 1 Example 2 The truss is distorted during fabrication because member bc is 0.5 in.short. k15 15415 415 6 -0.5 △Lo length changes in inches 90 6 -0.75 8Fe bar forces in kips D System Only bar bc is determined since it is the only bar that Q enters into the summation. 0.5 P System 0.5 过以你大子|国二本么年队
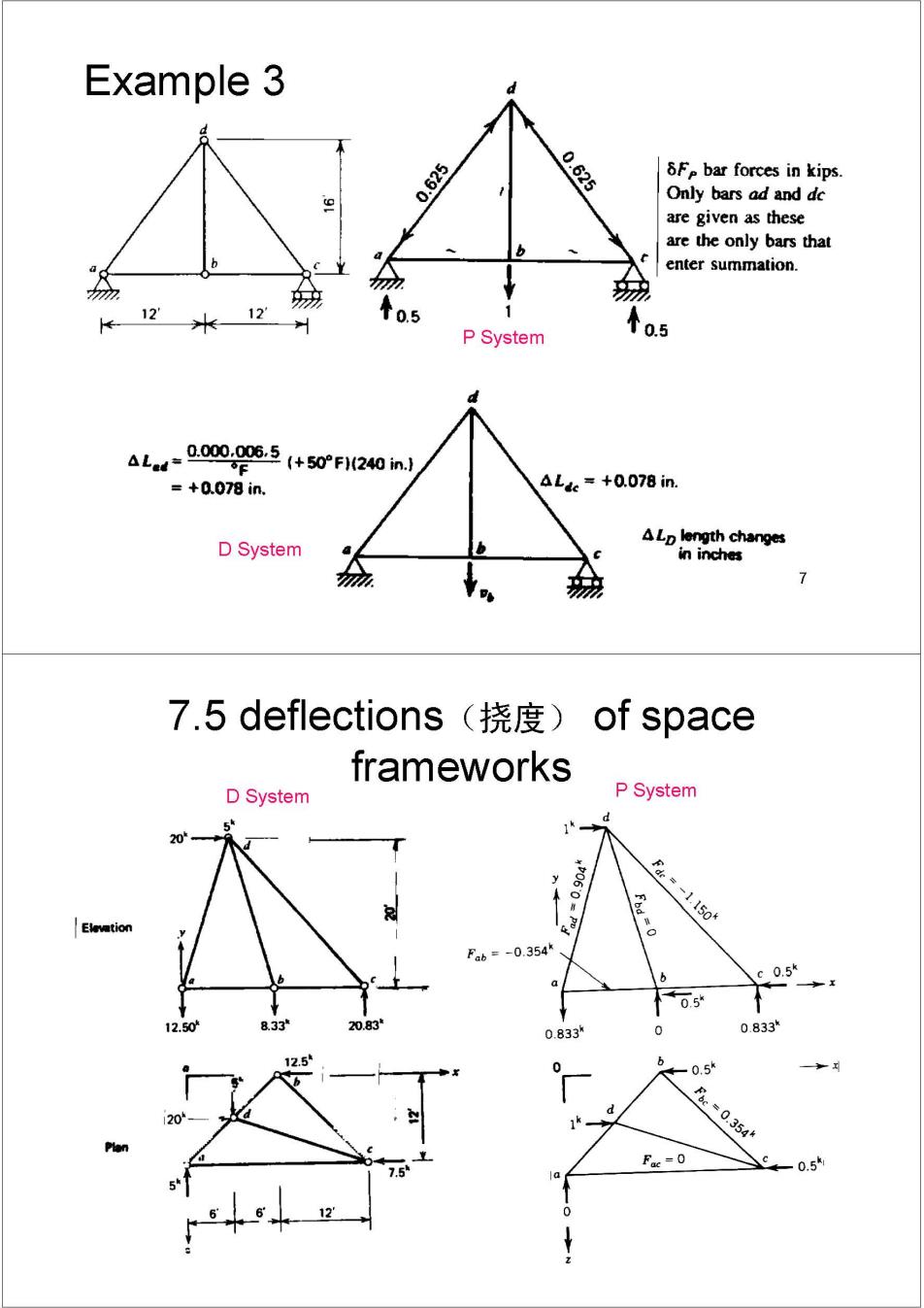
Example 3 0.625 0.625 Fe bar forces in kips. Only bars ad and dc are given as these are the only bars that enter summation. 12 12' ◆0.5 P System T0.5 aLa-0.00,006.5(+50F240inl =+0.078in. aLk=+0.078in. ALp length changes D System in inches > 7.5 deflections(挠度)of space frameworks D System P System 20 f=-1.150 Fab=-0.354 c0.5 0.5 12.50 8.33 20.83 0.833 0 0.833 0 b 0.5* d Fc=0.354 Fac-0 90.5
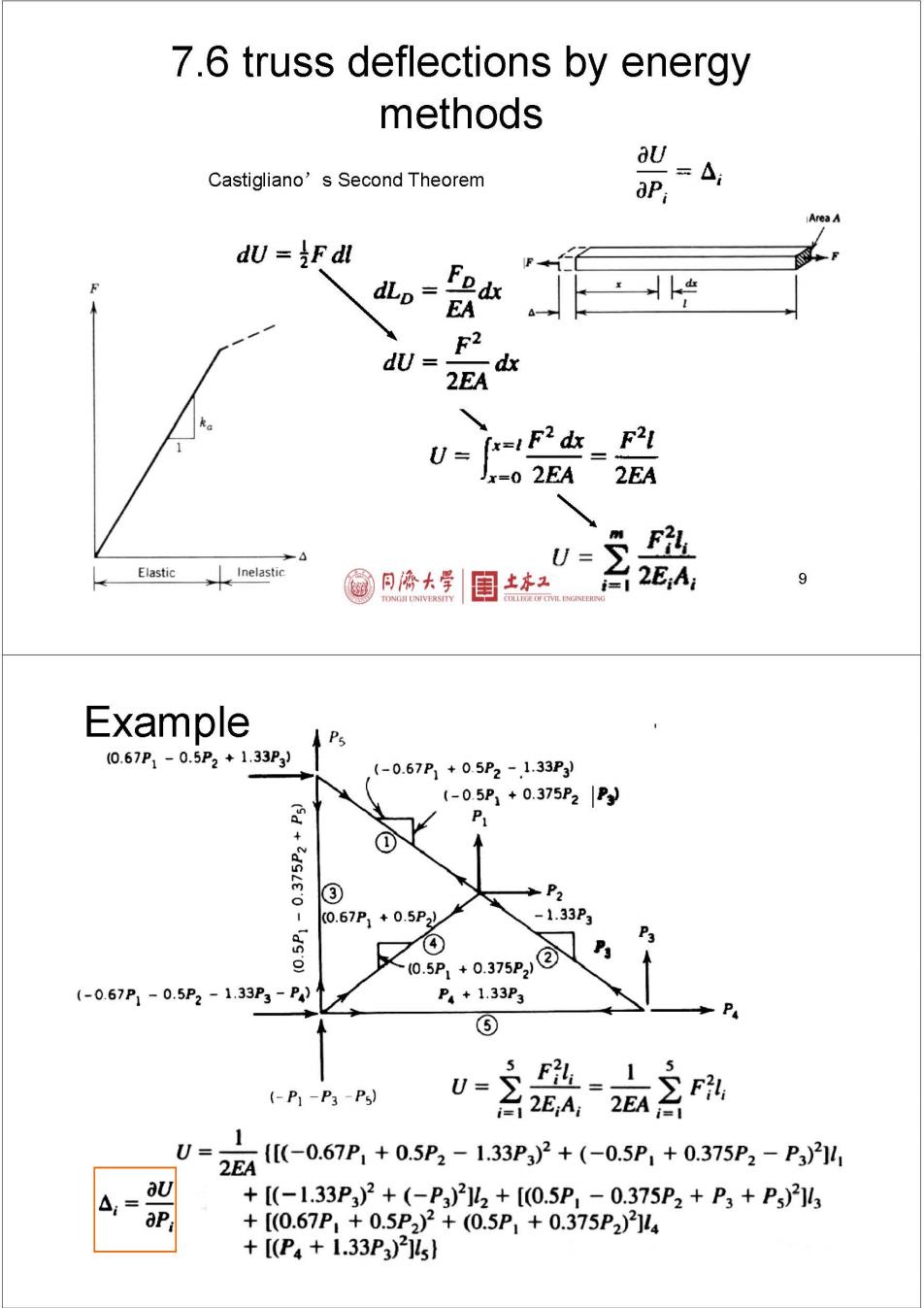
7.6 truss deflections by energy methods aU Castigliano's Second Theorem aPi Area A dU =iF dl dLp Fpdx EA 2 dU= dx 2EA U= 0 2EA 2EA U= N Elastic Inelastic 同停大学 土本2 i=1 2EA 9 Example Ps 0.67P1-0.5P2+1.33P (-0.67P1+05P2-1.33P) (-0.5P1+0.375P2P) N ① 2115 o ③ P2 0.67P1+0.5P2 -1.33P3 P3 e 05P,+0.375P@ (-0.67P1-0.5P2-1.33P3-P) P4+1.33P3 P ⑤ 1、 5 (-P1-P3-P5 器 U= 含F U=1 2EA ((-0.67P1+0.5P2-1.33P3)2+(-0.5P1+0.375P2-P3)21 aU △= +[(-1.33P3)2+(-P3)212+[0.5P1-0.375P2+P3+Ps)23 aP +[0.67P,+0.5P2)2+(0.5P1+0.375P2)]4 +P4+1.33P3)2]5}