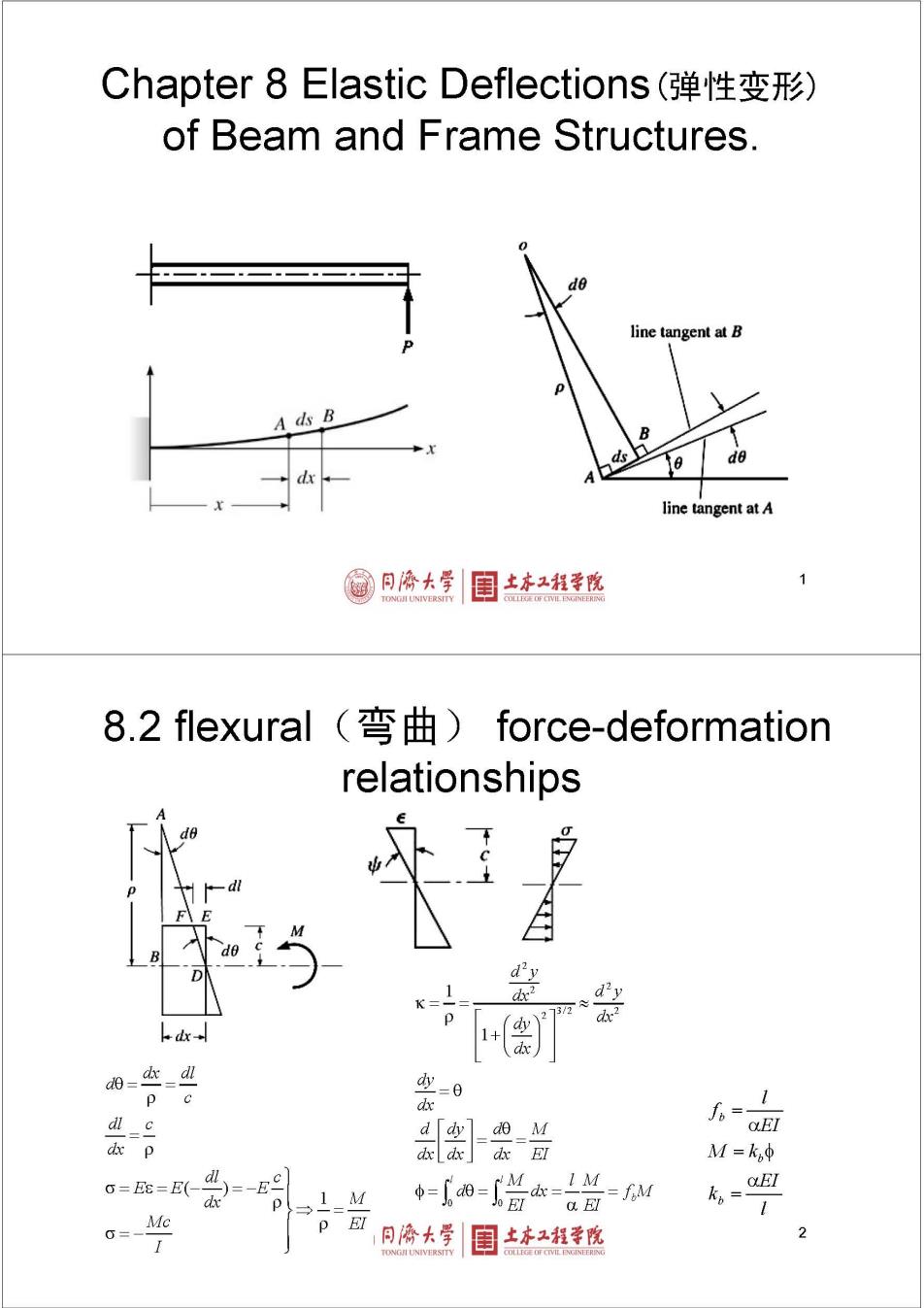
Chapter 8 Elastic Deflections(弹性变形) of Beam and Frame Structures. 0 d line tangent at B P P A ds B B x 45 0 d dx A line tangent at A 月济大学 自 土工程学院 TONGJI UNIVERSITY 8.2 flexural(弯) force-deformation relationships A d0 d F E M B d0 D d2 1 K ? = ≈ 3/2 P dx2 dx- 1+ d0= do al = pc dr dl_c d de M f= dxp dx d dx EI M=kp G=E8=E(-)=-E 1 M φ= d = 。 d = = P fM αEI kp= P EI 月济大学 土工程学院 2 TONGJI UNIVERSITY OGIRG

8.3 integration method(积分法) Load p 器=p:v=jpk+c d'M g=V:M=∫Vds+C2 dx =P 盟=:0=敛+C d'y M dx?El 袅=y=∫触+0 Positive slope p=0.3x-3 10 Rby V=0.15x2-3x+10 10 M=0.05x3-1.5x2+10x 9=∫尝k+G=言∫o0sr-15r2+1ok+G -ja+6-信0-as5s+6c y(x =0)produces C=0 y(x=10)produces C3= 土亦工程学院
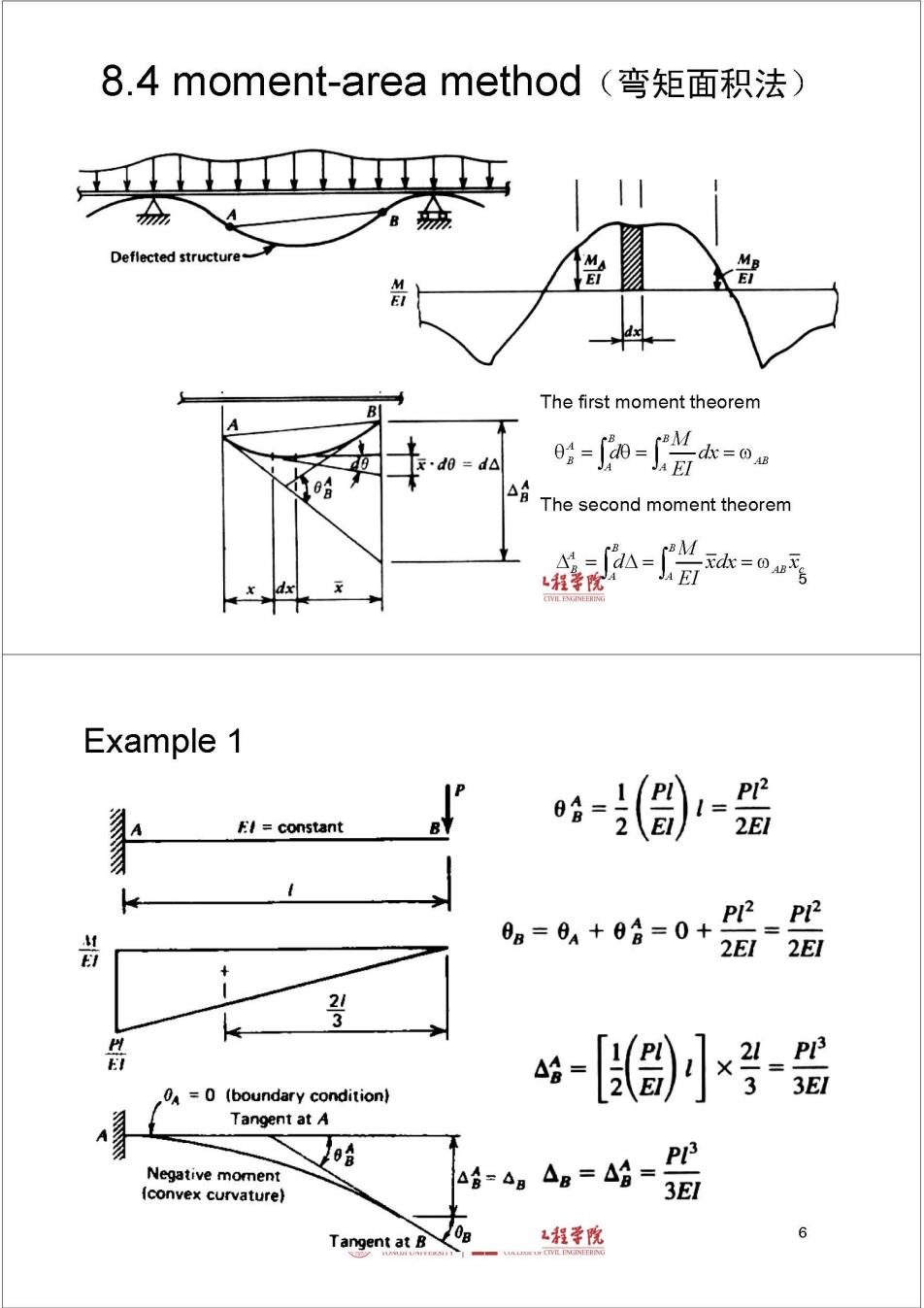
8.4 moment-area method(弯矩面积法) Deflected structure- M The first moment theorem .do =d 喘 = △日 The second moment theorem -岩 程学院A Example 1 constant 0= 2 始 PP2 PP M 0a=0A+0合=0+ 2E1 2E1 3 H PP 0=0 (boundary condition) 3El Tangent at A A 208 PL Negative moment △=4g △g=△g= (convex curvature) 3E/ Tangent at B 0g 气程学院
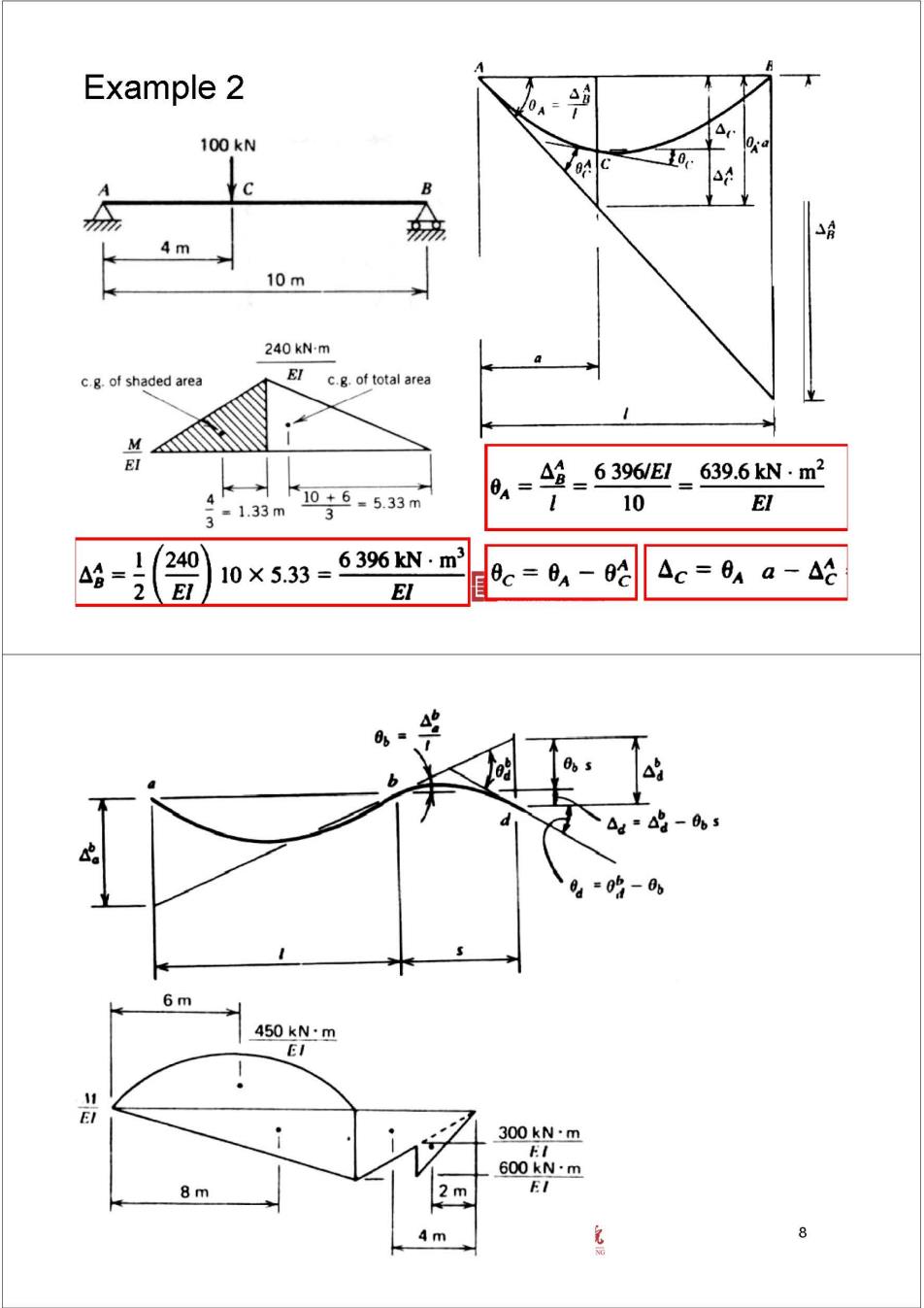
*7 Example 2 0 100kN 0 0 A B 4m 10m 240 kN-m c.g.of shaded area EI c.g.of total area M 6396/E1 639.6kN.m2 4 =1.33m 10+6=5.33m 10 El 3 3 A= 240 639%kN·m3 -2 10×5.33 El 0c=64- △c=64 a-At El 0%s b d -0s =0-0 6m 450 kN:m EI 1 1 300kN·m 600 kN.m 8m 2m EI 4m 丽
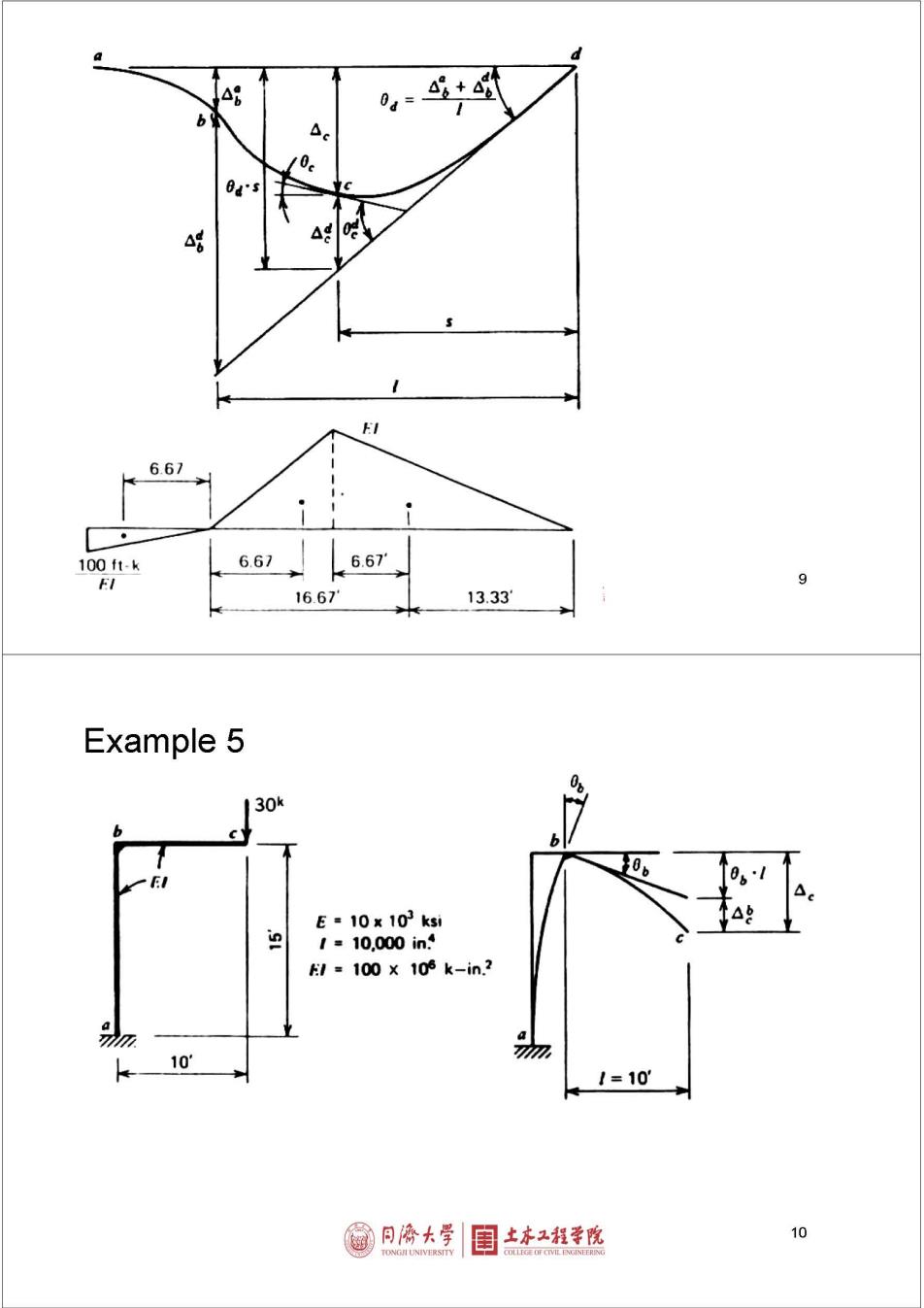
0=8+@ 6 Ba's △g 6.67 100f1-k 6.67 6.67 EI 9 16.67 13.33 Example 5 30k b E=10x103ks1 P 1=10.000in l=100×105k-in2 10 a 1=10 同像大学 目 土亦工程学院 10

6 2E1 Example 6 400kN→ EI 8m 1E=200GPa;1=4500×10-6m4 EI=900000kNm2 66=4 11 8.8 beam and frame deflections by complementary virtual work(虚余功) Virtual work vs.Real work 月海大学 目 土亦工程学院
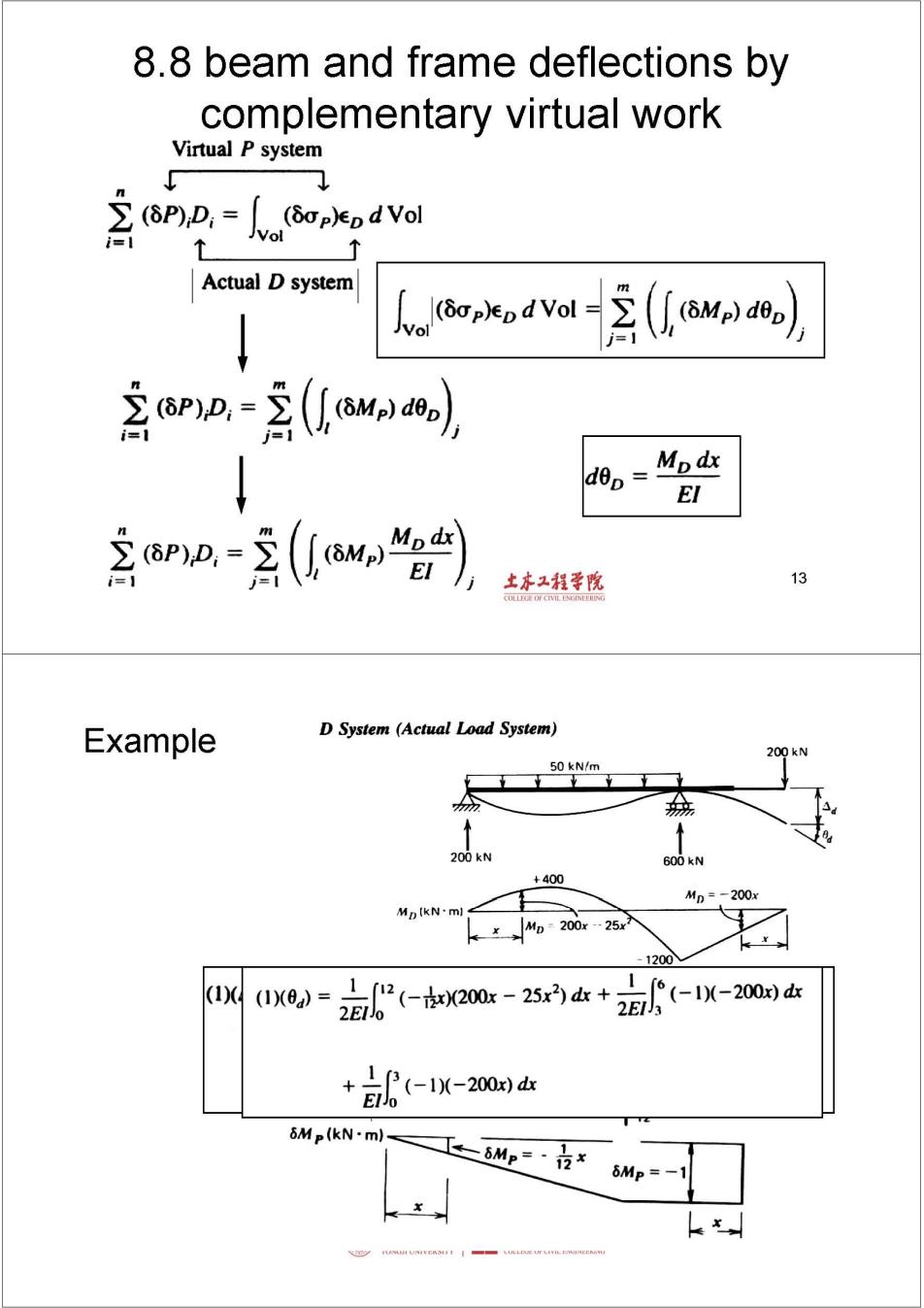
8.8 beam and frame deflections by complementary virtual work Virtual P system 2PD-人(opndVol Actual D system 人ak,dol-含(awwo】 2amo-2owa】 dep =Mpdx El Pn-2(lw"a 土水工程学院 13 Example D System (Actual Load System) 200kN 50 kN/m à 200kN 600kN +400 Mn=-200x Mp (kN-ml n200x25x2 -1200 (1) 00)=0(-kx20rc-250k+7-W-2w0 2Elo +款-X-20 δMp(kN~ml Mp=· 12* 6MP=-1

P=1 6 日 P=1 77977 (回 行 |国二 5 TONGJI UNIVERSITY Graph multiplication (图乘法) 三am-(cw增 M M:=xtga an M.M,dr =tga rM,dx =tgax·d2 do -50 yo M M,Mdx=tga·xon=nyo 0 同©大学 土本工程学院 16

Conditions: 1)The axis of the member is a straight line 2)EI=C 3)One of the two internal force function is a linear function(线性函数) 月大学 土本工程学院 17 a (6)2d-degree parabole tangent XC ·XC -4/2-/2 (I+a)/24牛bE a-子 0=d (d)2d-degree parabola (c)2d-degree parabola tangent- XC XC tangent 3/4 、L4 5l/8 +38 -l- 0=子 0-l (e)3d-degree parabola (f)nth-degree parabola tangent tangent -4/5 -{"+1)l/(n+2) aik g罗FONGI UNIVERSTY|arm
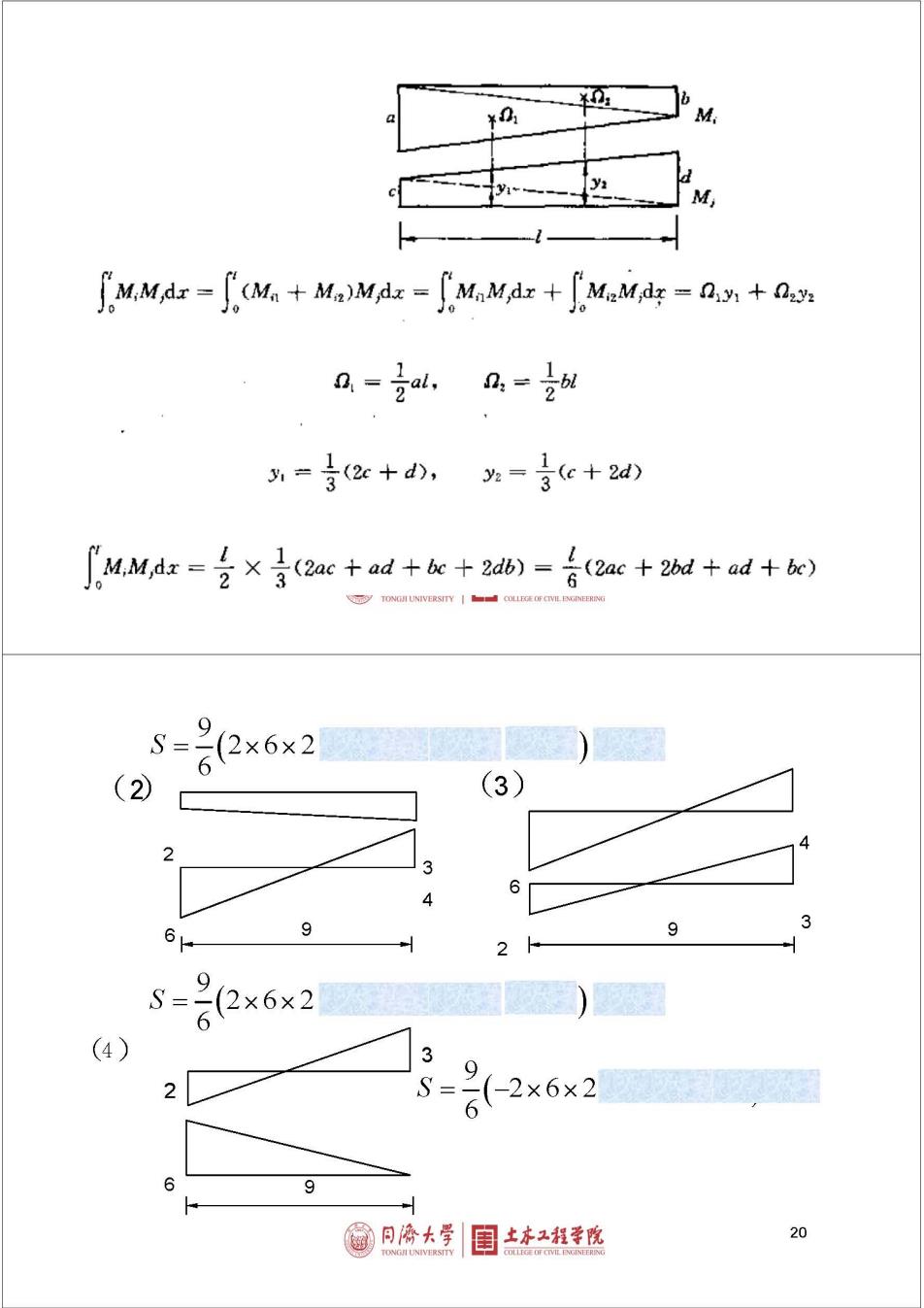
b M M M,Md-M。+M,Mk=M,aM+M.M=n,+a u. =吉(2c+d0,%=3c+2d) MMdz=台×合2ac+ad+c+2db)=合(2ac+2a+ad+be) 6 S= 2x6x2 6 (2) (3) 2 3 6 9 3 6 2 S=2x6x2 (4) 3 2 S- 2x6x2 6 9 @ 同像大学 目土本2程学院 20