
2014/5/12 Response to Harmonic and Periodic Excitations:SDOF Structural Dynamics .Classic topic in Structural Dynamics ·Excitations Chapter 3: ·Fundamental issue Significance in Earthquake Engineering EQM of linear viscous damped system Harmonic excitation mii+cu+ku=p(t) p(t)=posinot oR p(t)=Po cosor .Harmonic excitation .P is the amplitude or maximum value of the force p(t)=oR p(t)= Harmonic excitation of undamped system mii+cu+ku=po sin ot mii+ku=Po sin ot Initial conditions 叫=0)。=iO) 恩 REVIEW:Solution for linear ordinary REVIEW:Free vibration of Undamped SDOF differential equations of 2nd order with u(t)e" constant coefficients mii+ku=0 v"+ay'+by=c Solution=Complementary+Particular u(1)=Ae+Ae ler't pair motir st rea ·EQM mii+cu+ku=po sin ot u(t)=Acoso+Bsino! Solutions:u(1)=u()+u(1) 1
2014/5/12 1 Structural Dynamics Chapter 3: Response to Harmonic and Periodic Excitations Response to Harmonic and Periodic Excitations: SDOF • Classic topic in Structural Dynamics • Excitations • Fundamental issue • Significance in Earthquake Engineering • EQM of linear viscous damped system • Harmonic excitation • Harmonic excitation of undamped system • Initial conditions mu cu ku p t 0 mu ku p t sin 0 mu cu ku p t sin 0 p t p t sin 0 OR p t p t cos 0 (0) t u u 0 (0) t u u 0 p t p t sin 0 OR p t p t cos Harmonic excitation • p0 is the amplitude or maximum value of the force • ω is the exciting frequency or forcing frequency Source of harmonic excitation • Rotating machine with eccentric mass • Fourier series representation of any periodic excitation REVIEW: Solution for linear ordinary differential equations of 2nd order with constant coefficients Solution = Complementary + Particular y ay by c '' ' 0 mu cu ku p t sin u t u t u t c p • EQM: • Solutions: REVIEW: Free vibration of Undamped SDOF mu ku 0 ( ) st u t e 0 0 cos sin n n n u u t u t t 1 2 1 1 s t s t u t Ae Ae cos sin n n u t A t B t Introduce Euler’s pair noting that the response must real
2014/5/12 REVIEW:Free vibration of SDOF Free vibration of undamped SDOF u(t)=e" mii+cu+ku=0 心A = ⊕ u(0)=4cos is sino! Free vibration of underdamped SDOF Other scenario ·Critically damped Viscously dampingem 0=[u(0)1+o))+i(0)r]e✉ u()-[u(0)+(u(0)+i()):e ·Overdamped u0=ew(4em+4em) Coulomb damping syste %=a尽490 Other scenario Undamped SDOF mii+ku=po sinot Negative-damped system Complementary Solution u() u)-cov4sinh(o)cosh(o mii+ku=0 u.(1)=Acos@t+Bsin@t Particular solution:response due to Psin up(t)=Csinot+Dcosot 2
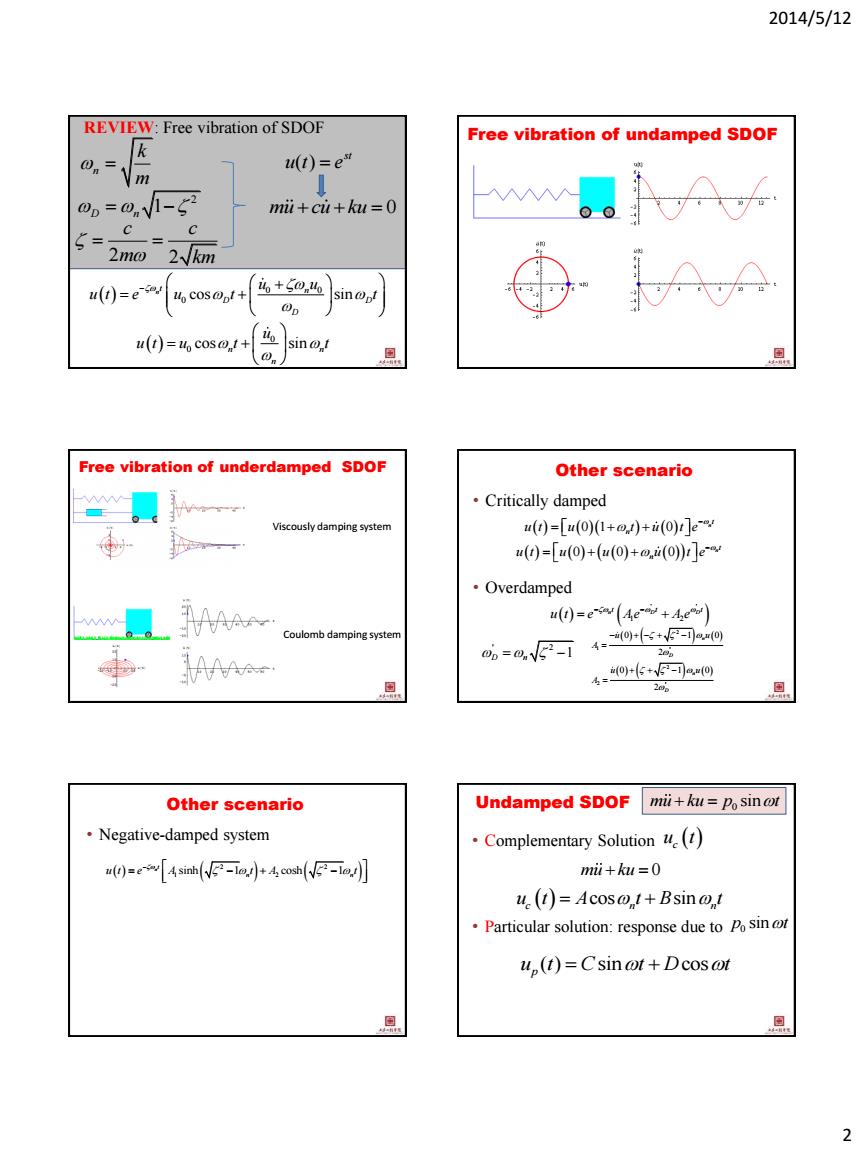
2014/5/12 2 REVIEW: Free vibration of SDOF mu cu ku 0 ( ) st u t e n k m 2 2 c c m km 0 0 0 cos sin n t n D D D u u u t e u t t 0 0 cos sin n n n u u t u t t 2 1 D n Free vibration of undamped SDOF Free vibration of underdamped SDOF Viscously damping system Coulomb damping system Other scenario • Critically damped • Overdamped 0 1 0 n t n u t u t u t e 0 0 0 n t n u t u u u t e ' ' 1 2 n D D t t t u t e Ae A e 2 1 ' 2 2 ' 0 1 0 2 0 1 0 2 n D n D u u A u u A ' 2 1 D n Other scenario • Negative-damped system 2 2 1 2 sinh 1 cosh 1 n t n n u t e A t A t Undamped SDOF 0 mu ku p t sin • Complementary Solution • Particular solution: response due to u t c mu ku 0 cos sin c n n u t A t B t 0 p t sin ( ) sin cos p u t C t D t

2014/5/12 ·Particular solution .Particular solution:response due to posin eady-d from the nditions becomes [(k-me)c-p]sinot+[(k-moi)D]coson-0 Input->Output c=-a P。sina→sin(om-) D=0 P6 cos@t→hcos(a-) Complete solution mi+kau=乃sin wt ·Complete solution )=)+,) 00ow9- ConstantsA,Bcan be determined as +是-oam 1 A=u(0 .Total response=transient response+ B=0)_凸o1a, steady state response 0.k1-(ola) .Transient response:vibration at the .Steady state response natural circular frequency,damp out 大1-(o1 .sine 1 Steady state response:vibration at the circular frequency of applied force Amplitude 1 2 k1-(o1o) - 人 Maximum static deformation Displacement response factor 3
2014/5/12 3 • Particular solution: response due to • From Physical observation: The steady-date vibration (the particular solution) after dissipation of transient vibration (eigenvibrations) from the initial conditions becomes harmonically varying with the same angular frequency ω as the excitation and with different amplitude and phase angle. 0 p t sin 0 0 0 0 sin sin cos cos Input Output p t u t p t u t • Particular solution 0 mu ku p t sin ( ) sin cos p u t C t D t 2 2 0 k m C p t k m D t sin cos 0 0 2 1 0 1 / n p C k D • Complete solution • Constants A, B can be determined as 0 mu ku p t sin 0 2 1 cos sin sin 1 / c p n n n u t u t u t p A t B t t k 0 2 0 0 / 1 / n n n A u u p B k 0 2 0 2 1 s 0 / 0 cos sin i 1 n 1 / / n n n n n n u p u t u t p t k t k • Complete solution • Total response = transient response + steady state response • Transient response: vibration at the natural circular frequency, damp out • Steady state response: vibration at the circular frequency of applied force • Steady state response • Amplitude • Maximum static deformation • Displacement response factor 0 2 1 sin 1 / n p u t t k 0 0 2 1 1 / n p u k 0 st p u k 0 2 1 1 / d st n u R u
2014/5/12 Displacement response factor ·Change of phase angle Dynamic magnification factor Dynamic amplification factor 1 R= ua 1-(0l0) 0=0,R=1 0=0n,R20 o/o.≥V5,Rp≤1 ·Resonance Beating phenomena:the transient and steady state response sometimes added to (o=a)u0=2(o1cose1-sina) out(out of phase) Harmonic vibration with viscous .Complementary solution damping u(1)=e s (Acospt+Bsinopl) ·Standard EQM ·Particular solution mii+cu+ku=po sin ot u (t)=Csinot+Dcosot 。Initial conditions =0) l。=i0) i+20.i- ·EQM i+25o+ou=Po sin ot m (i-)c-2cD-sina+[+(o-)
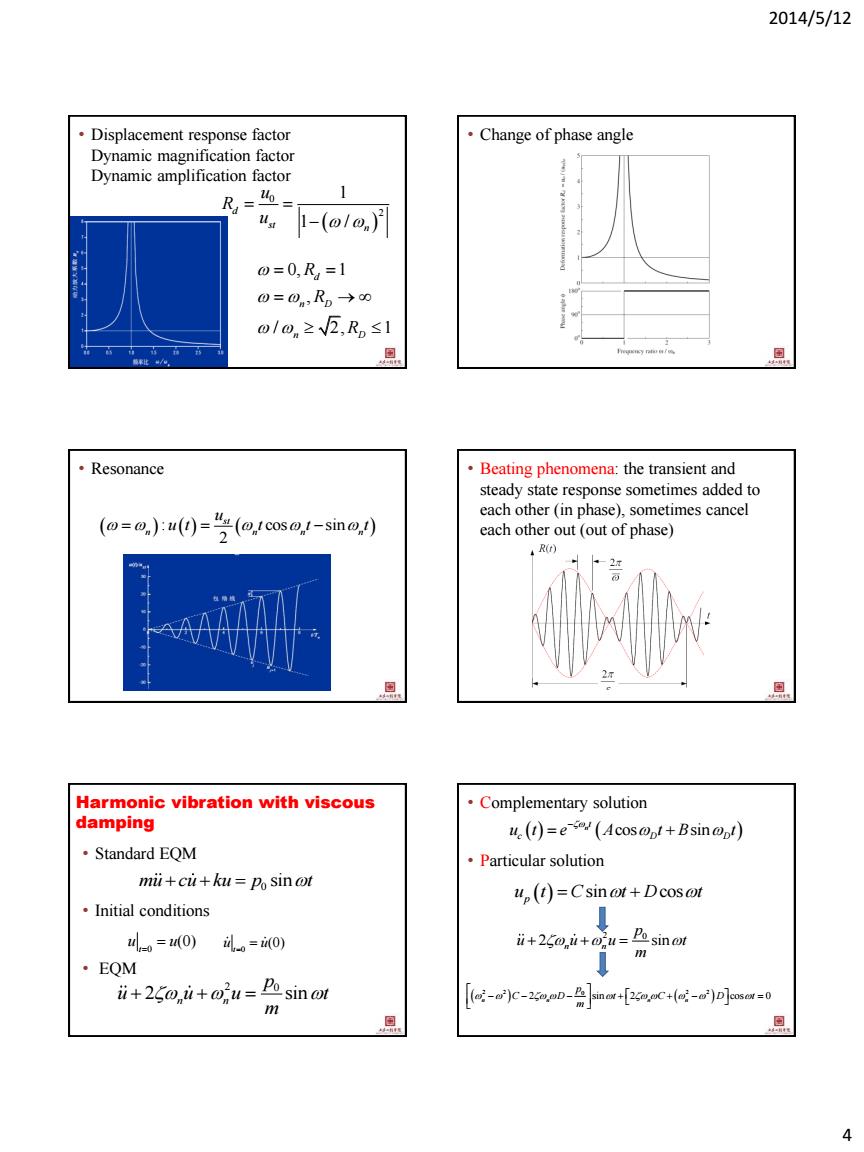
2014/5/12 4 0 2 1 1 / d st n u R u • Displacement response factor Dynamic magnification factor Dynamic amplification factor 0, 1 , / 2, 1 d n D n D R R R • Change of phase angle • Resonance : cos sin 2 st n n n n u u t t t t • Beating phenomena: the transient and steady state response sometimes added to each other (in phase), sometimes cancel each other out (out of phase) Harmonic vibration with viscous damping • Standard EQM • Initial conditions • EQM 0 mu cu ku p t sin 0 (0) t u u 0 (0) t u u 2 0 2 sin n n p u u u t m • Complementary solution • Particular solution cos sin n t c D D u t e A t B t sin cos p u t C t D t 2 2 2 2 0 2 sin 2 cos 0 n n n n p C D t C D t m 2 0 2 sin n n p u u u t m
2014/5/12 .From the above equation ·Complete solution --sp- u(t)=u+u u()=(Acos+Bsin)+(Csint+Dcosor) c--o1f月-ola Complete solution of undamped system u(t)=Acos+Bsin+(Csinot+Dcosor) x-oiaj-[la ·Total response ·Resonance C-(ola( p="-bl于(ele) C=0D=- ·Total response 0=(cm+Bsno小-2osm ·Initial conditions .Consider transient response or not? B-2 .Numerical calculation methods Expression of total response in resonance .Variation of response amplitude at resonance
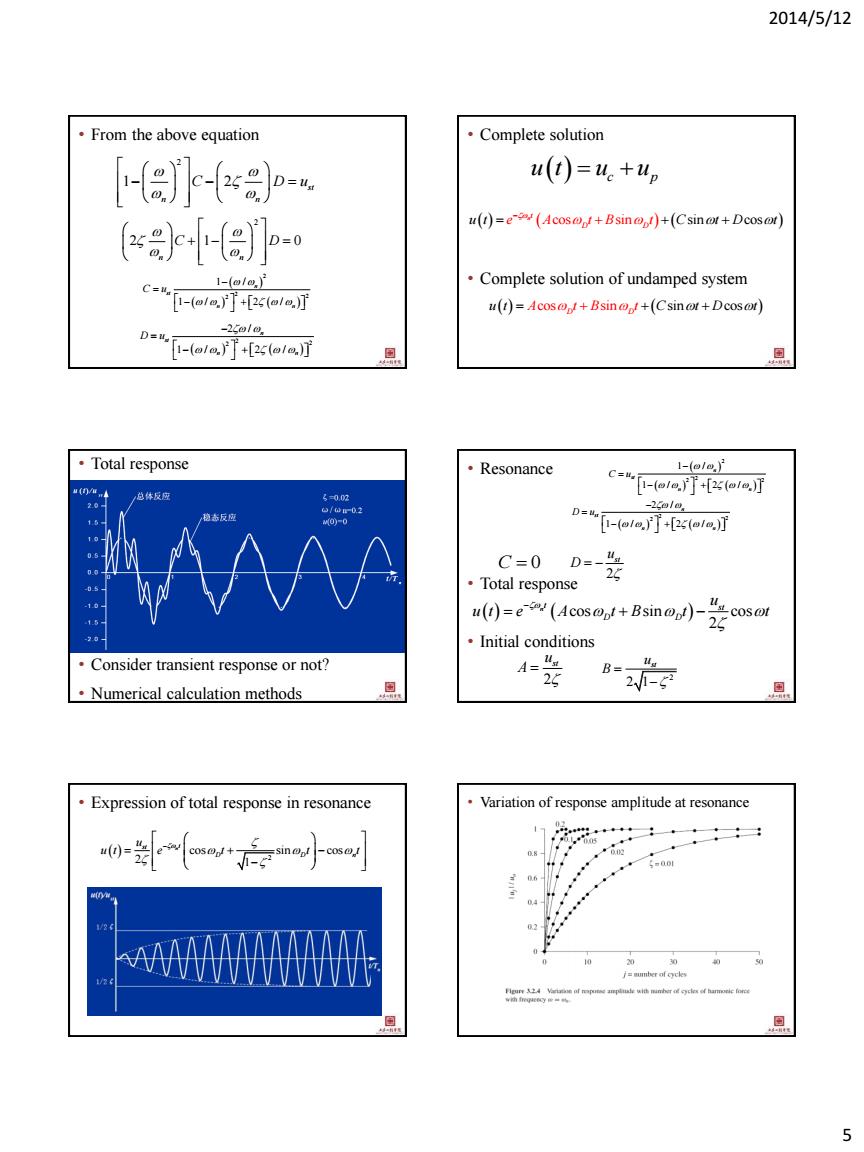
2014/5/12 5 • From the above equation 2 1 2 st n n C D u 2 2 1 0 n n C D 2 2 2 2 1 / 1 / 2 / n st n n C u 2 2 2 2 / 1 / 2 / n st n n D u • Complete solution • Complete solution of undamped system c p u t u u cos sin sin cos n t D D u t C e A t B t t D t u t C A t cos D D Bsin t sin t t Dcos • Total response • Consider transient response or not? • Numerical calculation methods • Resonance • Total response • Initial conditions 2 2 2 2 1 / 1 / 2 / n st n n C u 2 2 2 2 / 1 / 2 / n st n n D u C 0 2 st u D cos sin cos 2 n t st D D u u t e A t B t t 2 st u A 2 2 1 st u B • Expression of total response in resonance 2 cos sin cos 2 1 n st t D D n u u t e t t t • Variation of response amplitude at resonance

2014/5/12 Time duration for building up resonance Dynamic amplification factor response:experiment example u(t)=Csinot+Dcosot=usin(ot-) %=V@+D p=m() 1 = H1-(olo.J+[2c(olo.)J 1-(0lo.) .Dynamic amplification factor(displacement) Dynamic amplification factor(Velocity) Ry =to Vs 数 =。 -(o1a于+[2ge1aj Dynamic amplification factor(Acceleration) 1 R= 份e -olo)]+[25(olo.] Variation of dynamic amplification factor The DMF decrease with increase of with frequency ratio damping -0.01 Damping has much significant effect around resonance zone ·The maximum DMF does cur at 6
2014/5/12 6 • Time duration for building up resonance response: experiment example • Dynamic amplification factor u t C t D t u t sin cos sin 0 2 2 0 u C D 1 tan D C 0 2 2 2 1 1 / 2 / st n n u u 1 2 2 / tan 1 / n n • Dynamic amplification factor (displacement) 0 d st u R u 0 2 2 2 1 1 / 2 / st n n u u 2 2 2 1 1 / 2 / n n Rd • Dynamic amplification factor (Velocity) • Dynamic amplification factor (Acceleration) v d n R R 2 a d n R R 0 0 sin / cos / d v v d n u t R t p k u t R t R R p k • Variation of dynamic amplification factor with frequency ratio max 2 1 , 1 2 1 1 , 2 2 1 d d R R • The DMF decrease with increase of damping • Damping has much significant effect around resonance zone • When frequency ratio=1, DMF=1/2zeta • The maximum DMF doesn’t occur at ratio =1, meaning…
2014/5/12 ·Phase lag Phase lag represent the delay of A C-0H displacement response of the system with respect A线 to excitation. Physical meaning of the phase delay Resonant frequency Displacement resc Resonant response Bandwidth method for damping estimation Application of DMF:Example requency resp A rotating machine with the damping power bandw method ed or Amplitude nap 02T m,the vertic damping ratio is N=800r/ 20 eccentric mass P=30KN Determine the maximum vertical vibration amplitude? 1
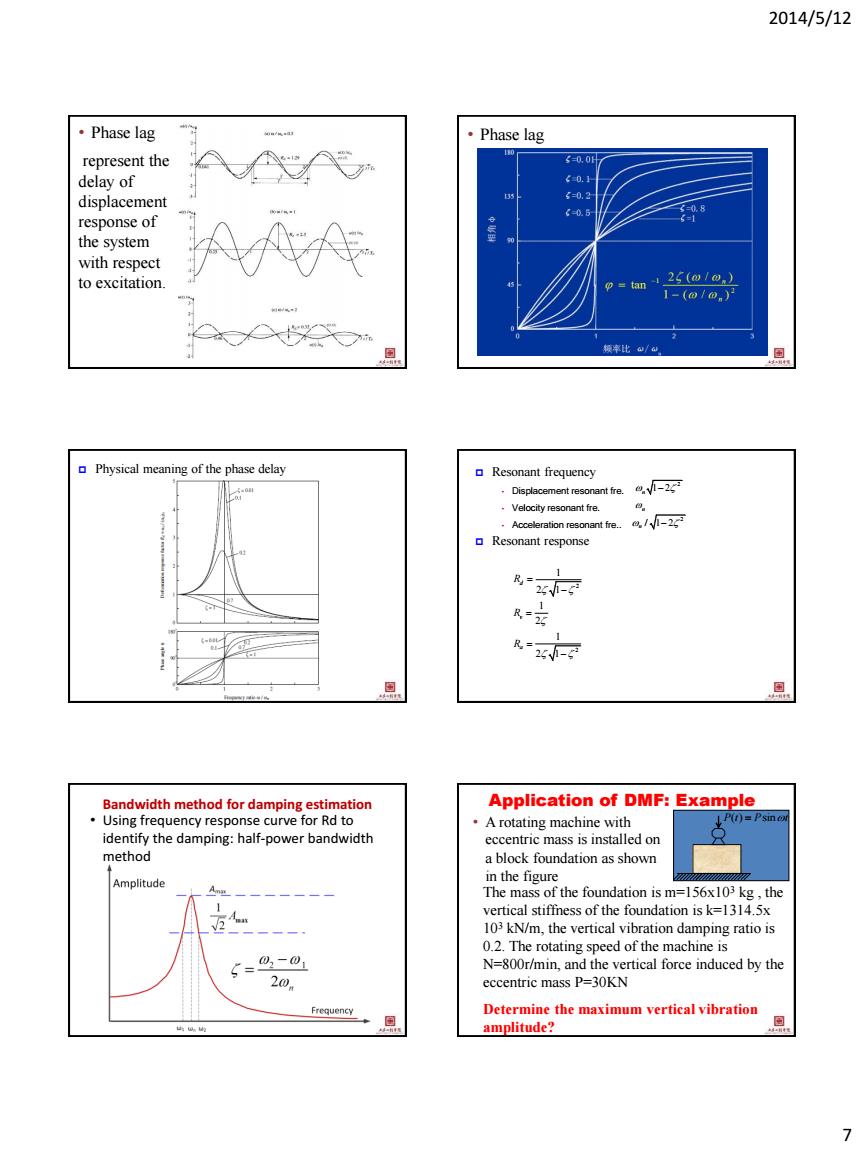
2014/5/12 7 • Phase lag represent the delay of displacement response of the system with respect to excitation. • Phase lag Physical meaning of the phase delay Resonant frequency • Displacement resonant fre. • Velocity resonant fre. • Acceleration resonant fre.. Resonant response 2 2 1 2 1 1 2 1 2 1 d v a R R R 2 1 2 n n 2 / 1 2 n Bandwidth method for damping estimation • Using frequency response curve for Rd to identify the damping: half-power bandwidth method Application of DMF: Example • A rotating machine with eccentric mass is installed on a block foundation as shown in the figure P t P t ( ) sin The mass of the foundation is m=156x103 kg , the vertical stiffness of the foundation is k=1314.5x 103 kN/m, the vertical vibration damping ratio is 0.2. The rotating speed of the machine is N=800r/min, and the vertical force induced by the eccentric mass P=30KN Determine the maximum vertical vibration amplitude?

2014/5/12 ·Solution Homework for week 3 30 %-k1B45x10=0228x0'm Problem 3.1,3.2 and 3.6 -=91.790/s a=60×2r=83.7811s R -2.49 1-(o1a2T+[2s(e1a月 %=Ry4,=2.49x0.0028×10°3=-0.0568mm 8
2014/5/12 8 • Solution: 2 2 2 1 2.49 1 / 2 / n d n R P t P t ( ) sin 3 3 30 0.0228 10 m 1314.5 10 st P u k 6 3 1314.5 10 91.79(1/ s) 156 10 n K m 2 83.78(1/ s) 60 N 3 0 2.49 0.0028 10 0.0568 d st u R u mm Homework for week 3 • Problem 3.1, 3.2 and 3.6