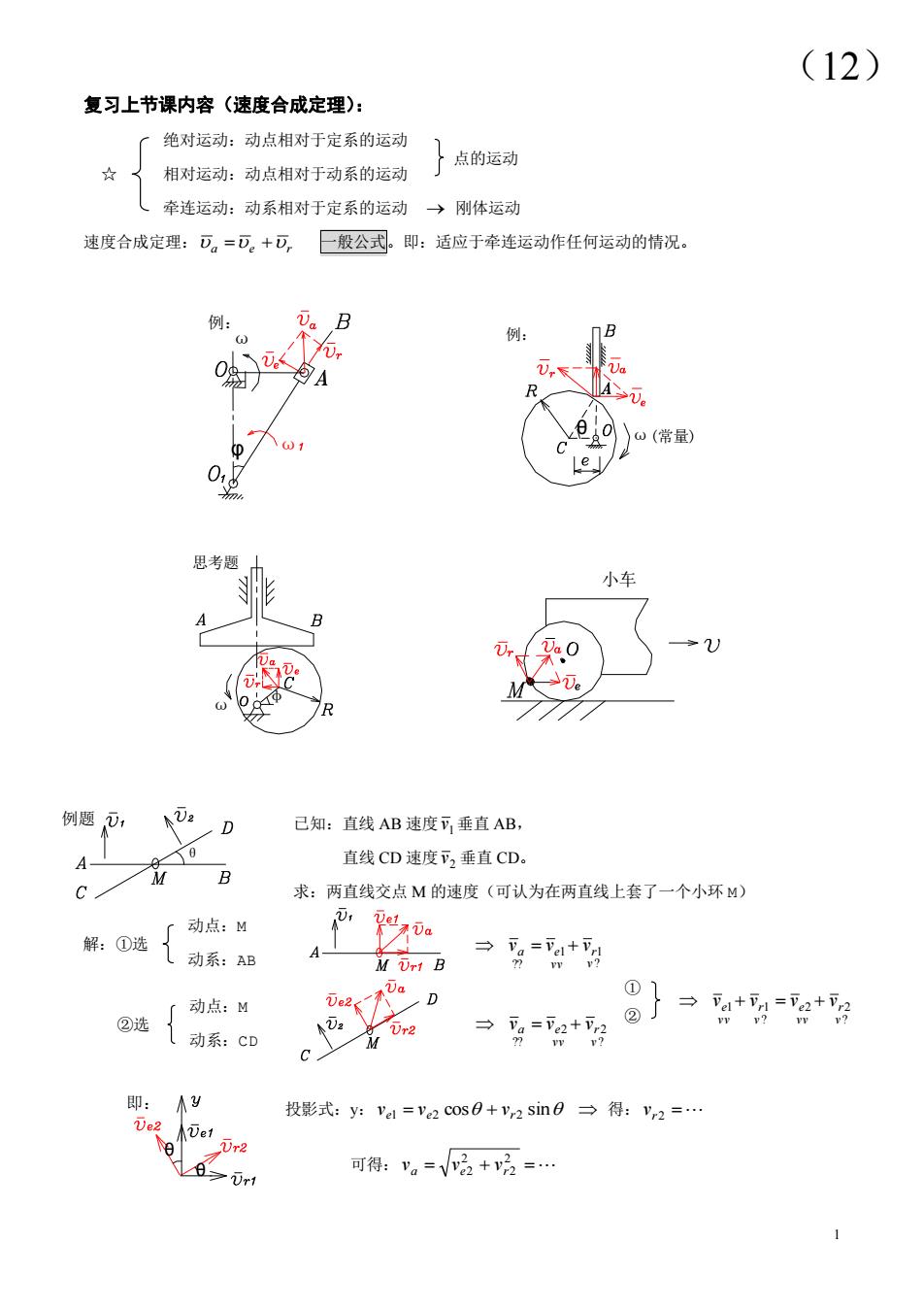
(12) 复习上节课内容(速度合成定理): 绝对运动:动点相对于定系的运动 ☆ 相对运动:动点相对于动系的运动 点的运动 (牵连运动:动系相对于定系的运动→刚体运动 速度合成定理:D。=D。+可,一般公式。即:适应于牵连运动作任何运动的情况。 例: B 4 0别 (常量) e 思考 小车 0 7R 例题, 已知:直线AB速度可垂直AB, A 直线CD速度可2垂直CD. B 求:两直线交点M的速度(可认为在两直线上套了一个小环M) 解:⑦选动点:M 动系:AB M Urt B g=4+ ②选 「动点: ⑧}+为=g+5 V: 动系:cD ⑦e →=+2 C 即: 投影式:y:e=ve2cos0+y2sin日→得:v2= 可得:v。=√2+哈2=…
1 ① ② ? 2 2 ? 1 1 v r vv e v r vv e v v v v ? 1 1 ?? v r vv a e v v v ? 2 2 ?? v r vv a e v v v (12) 点的运动 复习上节课内容(速度合成定理): 绝对运动:动点相对于定系的运动 相对运动:动点相对于动系的运动 牵连运动:动系相对于定系的运动 刚体运动 速度合成定理: a e r 一般公式。即:适应于牵连运动作任何运动的情况。 已知:直线 AB 速度 1 v 垂直 AB, 直线 CD 速度 2 v 垂直 CD。 求:两直线交点 M 的速度(可认为在两直线上套了一个小环 M) 动点:M 动系:AB 动点:M 动系:CD 投影式:y:ve1 ve2 cos vr2 sin 得: vr2 可得: va ve 2 2 vr 2 2 (12) 解:①选 ②选 例题 θ θ θ 即: ☆ φ ω ω 例: ω(常量) 例: θ φ ω 思考题 小车

$7-3、牵连运动为平移时点的加速度合成定理 速度合成定理:下。=可。+可,→与牵连运动形式无关,一般公式 (注:与速度合成定理不同,加速度与牵连运动形式有关) 有 时间1时:元。=可。+, 1+AM时:g=g+时 职:绝对加元=只-典+典 t+△t t时 动系平动 (物体平动) 动系平动有 -- @--a 即:an=a。+a 牵连运动为平移时点的加速度合成定理 例: a. 已知:OA=r,w=常量 a 求:图示时BC杆加速度 「动点、OA上A点 解:选{动系:BC牵:平动 有a,=a,+a,→展开:+a=a.+d,即:a=+ 有/口=0 a=r…o2 投影式:a.=a,cosp=ro2.cosp→即:ac 例: 己知:某瞬时ω及a 求:图示时BC杆ac c 解选动点:oa上a点 B 动系:BC(牵:平动) a0=r02 利用投影式, [x:(a),=(a),+(a,)x x:aasin+aa coso=ae (a=..) y:(aa)y=(ae)y+(a,)y y:ad coso-aasino=-a,(a,=.. (注意:投影的合成关系,不要与静力中的平衡方程混语) Rkā 产出已知:半轮之D及a //da 2
2 即:绝对加速度: t v v t v v t v v a r r t e e t a a t a 0 0 0 lim lim lim ② r r r t r r t a t t 2 0 0 lim lim ① e e e t e e t a t t 1 0 0 lim lim a y e y r y a x e x r x y: a a a x: a a a ( ) ( ) ( ) ( ) ( ) ( ) cos sin ( ) sin cos ( ) r r n a t a e e n a t a y: a a a a x: a a a a 有 2 0 a r a n a t 即: a ? ? e r n aa a a 有 2 a r a r n a t 有 a aa ae ar 展开: ? ? e r n a t aa a a a §7-3、牵连运动为平移时点的加速度合成定理 速度合成定理: a e r v v v 与牵连运动形式无关,一般公式 (注:与速度合成定理不同,加速度与牵连运动形式有关) 时间 t 时: a e r v v v t t 时: a e r v v v 即: aa ae ar 牵连运动为平移时点的加速度合成定理 已知: OA r ,ω =常量 求:图示时 BC 杆加速度 动点、OA 上 A 点 动系:BC(牵:平动) 有 aa ae ar 展开: e r n a t aa a a a 投影式: ae aa n cos r 2 cos 即: aBC 已知:某瞬时ω 及α 求:图示时 BC 杆 aBC 动点:OA 上 A 点 动系:BC(牵:平动) 利用投影式, (注意:投影的合成关系,不要与静力中的平衡方程混淆) 已知:半轮之 及 a 时 +Δ 动系平动 (物体平动) ω φ 例: α ω φ 例:例: 有 ∵动系平动 ∴有 解:选 解:选

求:图示时AB杆的aB R{地和 有:可=可+可,一可=+可码共“三个”未知量 :有a= “需进行速度分析 R B 心0 2=+5得:-ko=%0 C⑨ 77777777 R Rsin2 再由加速度分析:投影式:x:aa sin=a。cosp+a得:a。=…一aB 凸(介绍选择投影轴的技巧) ,①投影式不要写成∑a,=0 强调{②所得结果“士”表明指向假设是否正确 已知:OA与可0o=常量 例 60A 有BC=DE、,且BD=CE=I 来:图示时BDaD OBD a{融 1、速度分析: gg+2。=r,→得:=,==@。 又:=YB=BD.@BD六OD=' a=0 2、加速度分析:a。=ae+a,→ 展开:+耐=++a ag =rog a B D a"=aB =loB aB大 A 投影式:y:a sin30°=a6cos30°-a sin30 a (介绍:动点、动系的“反选”情况) 3
3 ? n r ? e r ? aa a a a 即: 2 2 2 Rsin v R v a n r r BD BD BD 2 2 0 BD n B n e o n a t a a a l a r a ∴ l r BD v o e BD 得 ae t BD a t e BD 求:图示时 AB 杆的 a AB 动点:AB 上 A 点 动系:半轮(牵:平动) 有: aa ae ar 共“三个”未知量 再由加速度分析:投影式: n aa ae ar x: sin cos 得: aa aAB ①投影式不要写成 ax 0 ②所得结果“±”表明指向假设是否正确 已知:OA=r O =常量 有 BC DE、 且 BD CE l 求:图示时 动点:OA 上 A 点 动系:BC(牵:平动) 1 、 速 度 分 析 : va ro 得: e r a o v v v r 又:∵ e B BD BD v v 2、加速度分析: aa ae ar 投影式:y: sin 30 cos 30 sin 30 n e t e n aa a a (介绍:动点、动系的“反选”情况) φ φ ω 例 ω α 解:选 注:∵有 R a n r r 2 ∴需进行速度分析 ? e r ? a v v v 得: sin sin v v v e r 强调 (介绍选择投影轴的技巧) 解:选 ? r ? a e v v v 展开: ? r n e ? t e n a t aa a a a a
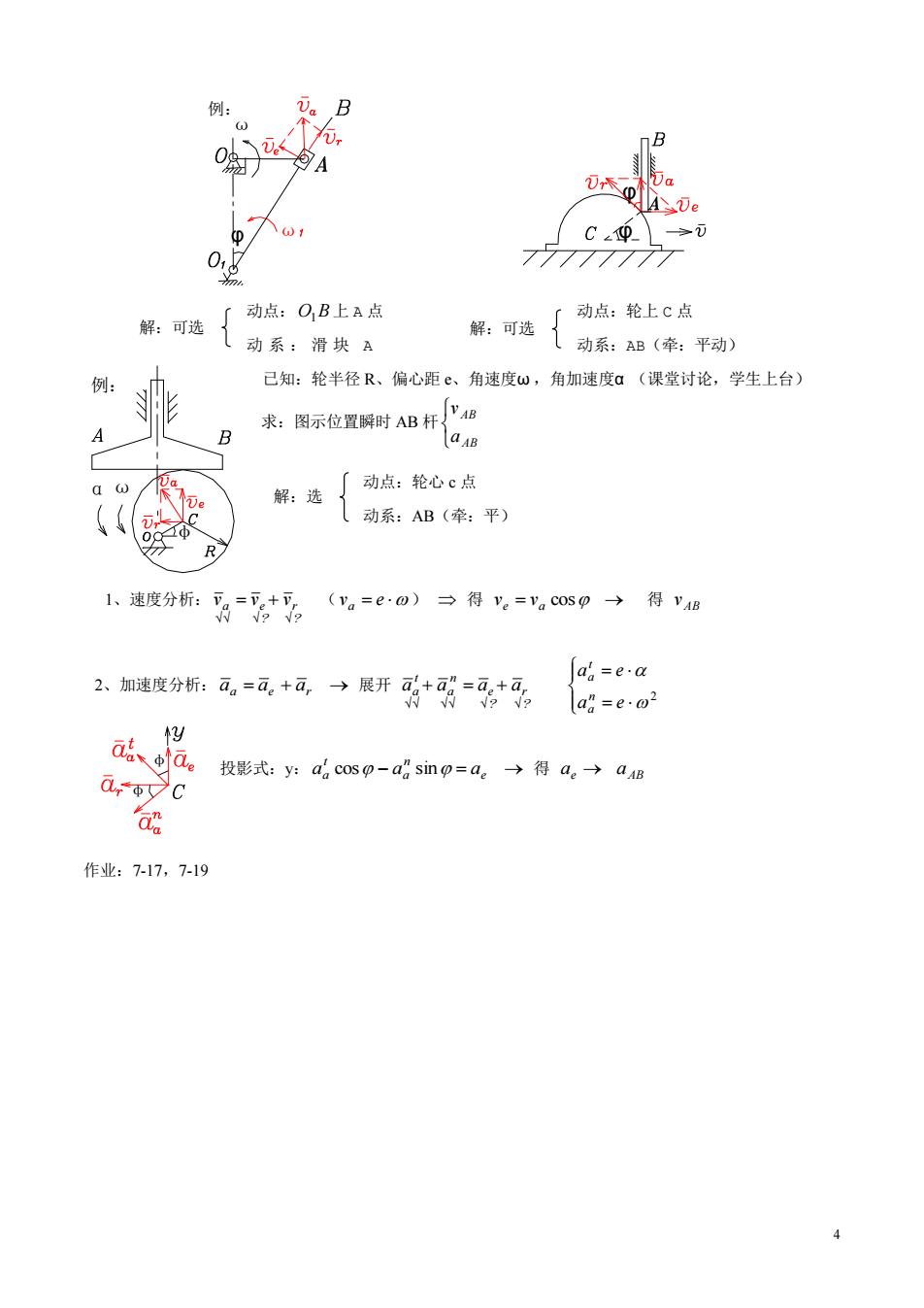
i。B 77777777 解:可选厂动点:QB上A点 「动点:轮上C点 (动系:滑块A 解:可选{动系:B(率:平动》 已知:轮半径R、偏心距e、角速度w,角加速度a(课堂讨论,学生上台) 来际时a出打化 a 「动点:轮心c点 解,选动系:AB(牵:平) 1、速度分折:=。 (va=e0)→得ye=v。cosp→得vB 2、加速度分折:a,=可。+ā→展开码+可码=+可。 =e.a las=e.o y a影d0-asmp=a→得a→a ar oc Cre 作业:7-17,7-19 4
4 求:图示位置瞬时 AB 杆 AB AB a v φ ω ω 例: 解:可选 解:可选 动点: O1B 上 A 点 动点:轮上 C 点 动 系 : 滑 块 A 动系:AB(牵:平动) 已知:轮半径 R、偏心距 e、角速度ω ,角加速度α (课堂讨论,学生上台) 动点:轮心 c 点 动系:AB(牵:平) 投影式:y: aa t cos aa n sin ae 得 ae aAB 作业:7-17,7-19 φ αω 例: φ φ 解:选 1、速度分析: ? r ? a e v v v ( va e ) 得 ve va cos 得 AB v 2、加速度分析: aa ae ar 展开 ? r ? e n a t aa a a a 2 a e a e n a t a φ φ