第二次课 求剪力弯矩方程并画剪力弯矩图(以下两个做验证用) 1. Q(x)=-3kN Q(x)=R-P=7kN M(x)=-3x M(x)=7x-6 Q(x)=g2.4-x)-R。=19-10x M)=R,(24-x)-7924-x2=12-5x-524-x2 P=3kN m=3.6kN·m9=10kVm 6ma6m12m RA 吃 O AN 圆sN 1.2kN.m §4.5载荷集度、剪力和弯矩间的关系 dO(x)-q(x) dx
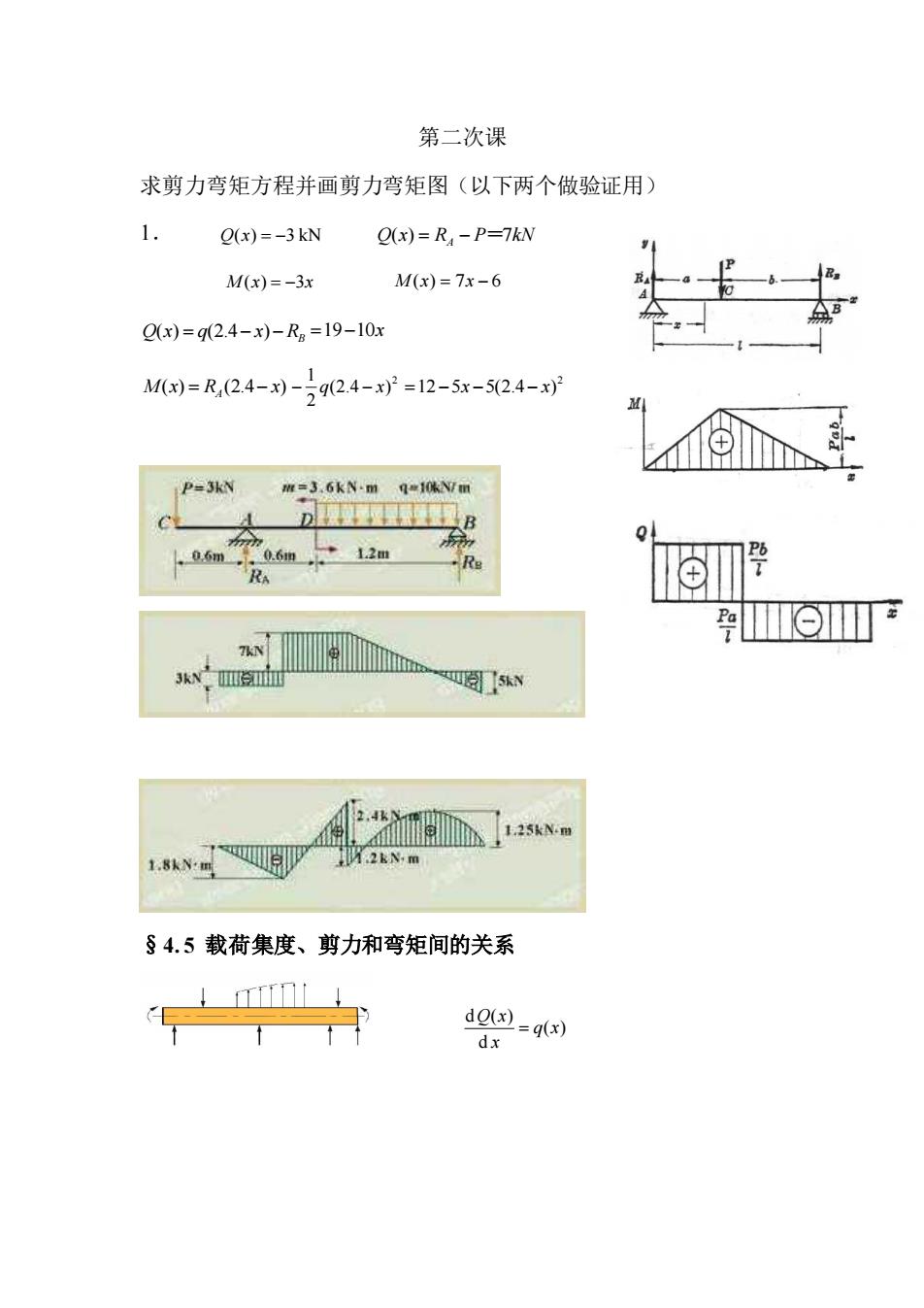
第二次课 求剪力弯矩方程并画剪力弯矩图(以下两个做验证用) 1. Q(x) = −3 kN Q(x) = RA − P=7kN M (x) = −3x RB Q(x) = q(2.4− x)− =19−10x M(x) R (2.4 x) = A − 2 (2.4 ) 2 1 − q − x 2 =12−5x −5(2.4− x) §4. 5 载荷集度、剪力和弯矩间的关系 ( ) d d ( ) q x x Q x = M (x) = 7x − 6

dM因=Q) dx d M(x=q(x) Me)+dMe) 由微分关系可得以下结论 (1)若qx)=0 Qx)=常数,剪力图为水平线:M)为一次函数,弯矩图为斜直线 2)若qx)=常数 Q(x)为一次函数,剪力图为斜直线;M似为二次函数,弯矩图为抛物线 当q)>0(向上)时抛物线是下凸的; 当q)<0(向下)时抛物线是上凸的:雨全形线 (3)在剪力Q为墨处,弯矩M取极值。 注意:以上结论只在该段梁上无集中力或集中力偶作用时才成立。 推导有集中力和集中力偶时的Qx),M:) (④)在集中力作用点:剪力图有突变,突变值即为集中力的数值, 突变的方向沿着集中力的方向,弯矩图在该处为折点。 (⑤)在集中力偶作用点:对剪力图形状无影响;弯矩图有突变,突 变值即为集中力偶的数值
由微分关系可得以下结论 (1) 若 q(x) = 0 Q(x) =常数,剪力图为水平线;M(x) 为一次函数,弯矩图为斜直线。 (2) 若 q(x) = 常数 Q(x) 为一次函数,剪力图为斜直线;M(x) 为二次函数,弯矩图为抛物线。 当 q(x) > 0(向上)时,抛物线是下凸的; 当 q(x) < 0(向下)时,抛物线是上凸的;雨伞形状 (3) 在剪力 Q 为零处, 弯矩 M 取极值。 注意: 以上结论只在该段梁上无集中力或集中力偶作用时才成立。 推导有集中力和集中力偶时的 Q(x),M(x) (4) 在集中力作用点:剪力图有突变,突变值即为集中力的数值, 突变的方向沿着集中力的方向,弯矩图在该处为折点。 (5) 在集中力偶作用点: 对剪力图形状无影响;弯矩图有突变,突 变值即为集中力偶的数值。 ( ) d d ( ) Q x x M x = ( ) d d ( ) 2 2 q x x M x =
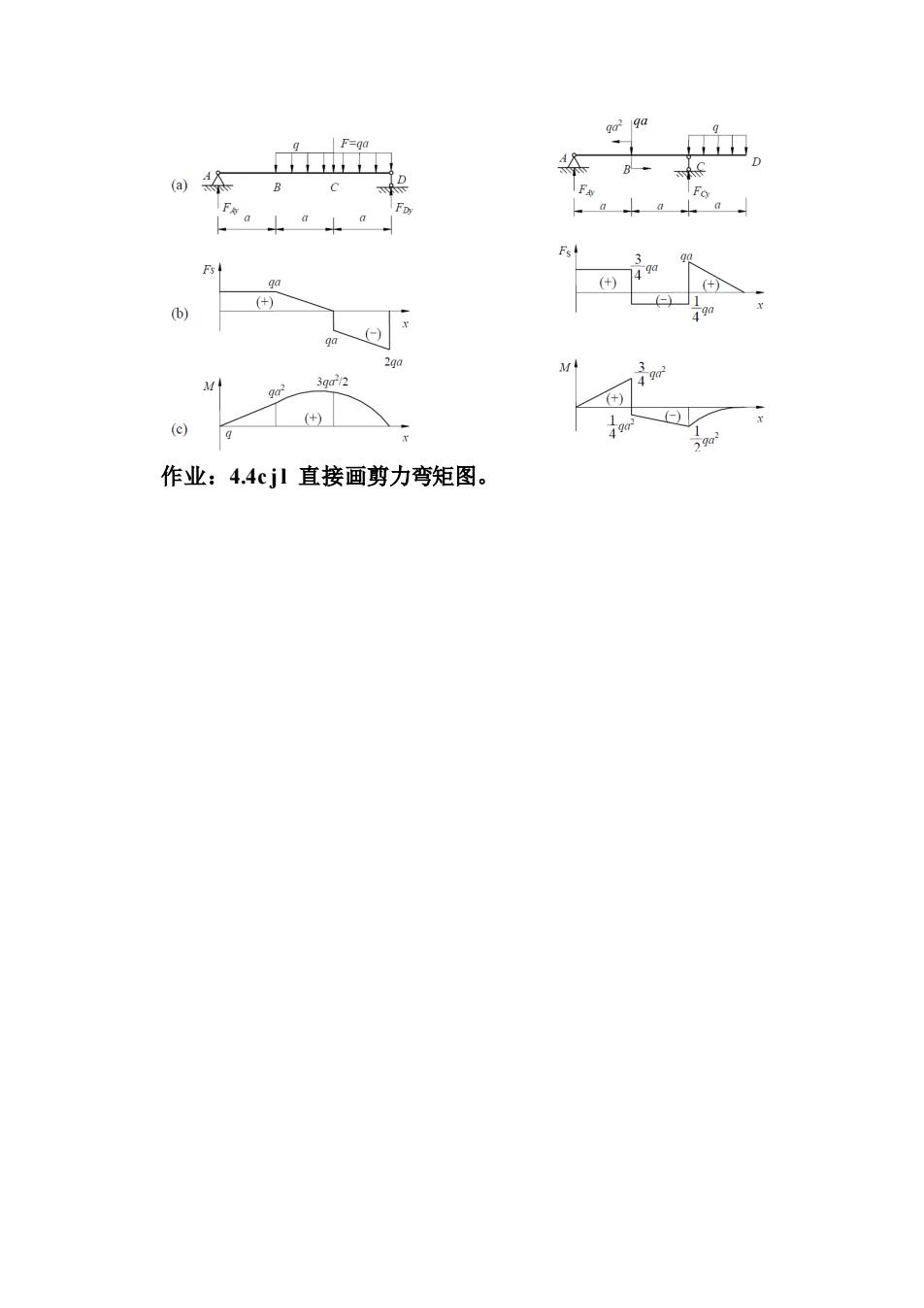
(a) 作业:4.4cjl直接画剪力弯矩图
作业:4.4c j l 直接画剪力弯矩图