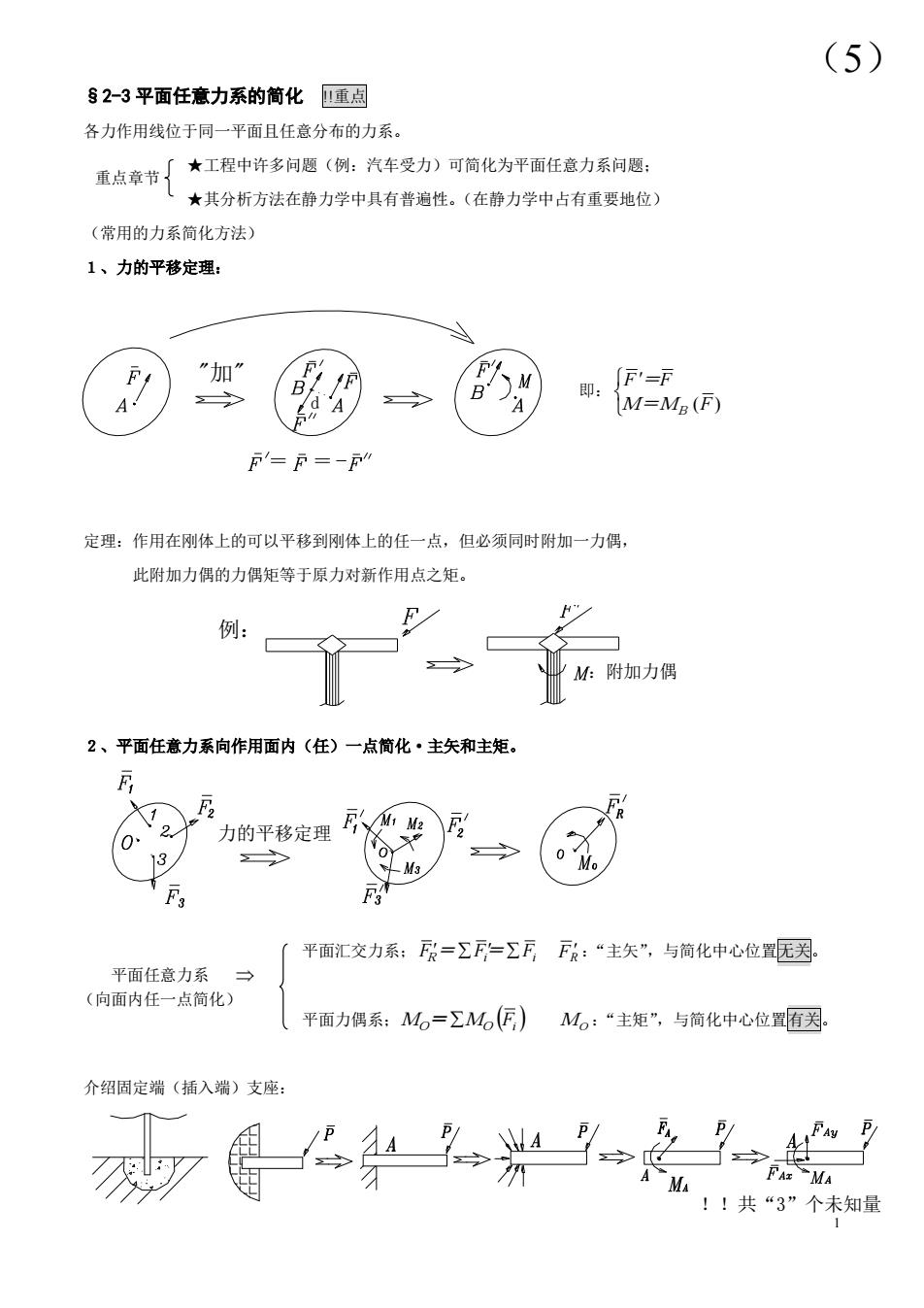
(5) 82-3平面任意力系的简化重点 各力作用线位于同一平面且任意分布的力系。 重点章节 ★工程中许多问题(例:汽车受力)可简化为平面任意力系问题: ★其分析方法在静力学中具有普遍性。(在静力学中占有重要地位) (常用的力系简化方法) 1、力的平移定理: 加 5=- 定理:作用在刚体上的可以平移到刚体上的任一点,但必须同时附加一力偶, 此附加力偶的力偶矩等于原力对新作用点之矩。 例: M:附加力偶 2、平面任意力系向作用面内(任)一点简化·主失和主矩。 O. “力的平移定理 13人 07 M3 平面汇交力系:=ΣF-Σ万F:“主矢”,与简化中心位无闲 平面任意力系 (向面内任一点简化) 平面力偶系;Mo=ΣM(匠)Mo:“主矩”,与简化中心位置有 介绍固定端瑞(插入端)支座: A-MA FAzMA !!共“3”个未知量
1 §2-3 平面任意力系的简化 !!重点 各力作用线位于同一平面且任意分布的力系。 ★工程中许多问题(例:汽车受力)可简化为平面任意力系问题; ★其分析方法在静力学中具有普遍性。(在静力学中占有重要地位) (常用的力系简化方法) 1、力的平移定理: 即: M=M (F) F =F B 定理:作用在刚体上的可以平移到刚体上的任一点,但必须同时附加一力偶, 此附加力偶的力偶矩等于原力对新作用点之矩。 2、平面任意力系向作用面内(任)一点简化·主矢和主矩。 平面汇交力系; FR = Fi = Fi FR :“主矢”,与简化中心位置无关。 平面力偶系; MO = MO Fi MO :“主矩”,与简化中心位置有关。 介绍固定端(插入端)支座: d "加" 例: :附加力偶 力的平移定理 !!共“3”个未知量 (5) 重点章节 平面任意力系 (向面内任一点简化)

3、平面任意力系简化结果分析 平面任意力系∫主矢:F=Σ (向一点简化)主矩:Mo=ΣM() 厂①F=0,M≠0力系简化为一力偶,此时主矩与0点无关 ②F3≠0,M。=0力系简化为一合力,通过0点的主矢即为合力 ③F≠0,M。≠0→可进一步简化 人④=0,Mo=0力系平衡 F 分析③FR≠0,M。≠0 d=Mo/FR 今进一步简化为一合力。 注:合力作用线在0点何侧,需综合F'与M。来判断。 即:平面任意力系简化共有三种情况 力偶 (注意:空间力系不同!) L平衡 Mo=ΣMo(E) (Mo(FR)=FRd=Mo 即:Mo(匠上∑Mo(瓦)→“合力矩定理” $2-4平面任意力系的平衡条件和平衡方程重点 〔主失:限=0 →力系平衡(平面任意力系平衡的充要条件:力系的主矢和对任一点主矩均为零) 、主矩:M4o=0 ∑F=0 ∑F=0 )“投影式” 三个独立方程,可求解三个未知量! 平衡方程( ∑Mo(E)=0(简:∑Mo=0)→“力矩式” 其它形式: ∑M4=0 ☆、“二矩式 ∑MB=0 o090 相互独立条件:A、B两点连线不垂直轴。 ∑E=0 ∑M4=0 91 ☆、“三矩式” ∑MB=0 ∑Mc=0 BC相互独立条件:A、B、C三点不共线
2 主矢: FR =0 主矩: MO =0 θ≠90° 相互独立条件: 、 两点连线不垂直 轴。 3、平面任意力系简化结果分析 平面任意力系 主矢: FR = Fi (向一点简化) 主矩: MO = MO Fi ① FR =0 ,MO 0 力系简化为一力偶,此时主矩与O点无关 ② F 0,M O =0 R 力系简化为一合力,通过O点的主矢即为合力 ③ 0 O 0 F R ,M 可进一步简化 ④ F =0,M O =0 R 力系平衡 分析③ 0 O 0 F R ,M 即: O R R R d M F F F 进一步简化为一合力。 注:合力作用线在O点何侧,需综合 Fa与MO 来判断。 即:平面任意力系简化共有三种情况 (注意:空间力系不同!) 又: O R R O O O i M F F d M M M F ( ) ( ) 即: MO FR = MO (Fi ) “合力矩定理” §2-4 平面任意力系的平衡条件和平衡方程 !!重点 力系平衡(平面任意力系平衡的充要条件:力系的主矢和对任一点主矩均为零) “投影式” 三个独立方程,可求解三个未知量! 平衡方程 (简: M O 0 ) “力矩式” 其它形式: ☆、“二矩式 ☆、“三矩式” 相互独立条件: 、 、 三点不共线。 力 力偶 平衡 Fx 0 Fy 0 MO (Fi ) 0 M A 0 M B 0 Fx 0 M A 0 M B 0 MC 0

F8? 已知:P、Q、a、6 例: B 求:A、B两处反力 解:整体(也可分析AC)(应注意到BC为“二力构件” 0入 ∑F=0Fs-Fa cos0=0 ∑F,=0F+Fn sin0-P-Q=0 >解得:{ >M=0 Fg cos0.4a.1g0-P.2a-0.3a=0 Fa Fg sin0.4a (注:也可将上式中的前两式置换,即:由∑Mg=0→求F,;由∑M=0→求Fy; 也即可采用“三矩式”求解。但需注意:虽可写出多个平衡方程,而独立的方程数目只有3个) 例: A☐C 求:A、B两处反力、 EAx 解:AB(简支梁) aa B ∑F,=0F=0 ∑M4=0-q-2aa-P.2a-M+Fg4a=0→Fg ∑F,=0(或∑MB=0)F-q2a-P+FB=0→F (注意:力偶M的投影式和力矩式) 求:A处反力 例 解:整体(悬臂梁) ∑F=0Fa+293-Fos30=0→Fa A q ∑F,=0F-P-Fsin30°=0→F ∑M4=0M-793-1-M+Fcos30°.3+fsn30-1=0→M, (注:书中将分布载荷q变化为集中载荷画在图中不妥)
3 已知:P、Q、a、θ 求:A、B两处反力 解:整体(也可分析AC)(应注意到BC为“二力构件”) Fx 0 FAx FB cos 0 Fy 0 FAy FB sin P Q 0 解得: M A 0 FB cos 4a tg P 2a Q 3a 0 FB sin 4a (注:也可将上式中的前两式置换,即:由 MB =0 求FAx, ;由 MC =0 求FAy ; 也即可采用“三矩式”求解。但需注意:虽可写出多个平衡方程,而独立的方程数目只有 3 个) 求:A、B两处反力、 解:AB(简支梁) 0 0 Fx FAx A B FB M 0 q 2a a P 2a M F 4a 0 y B Ay P FB FAy F 0 (或 M 0) F q 2a 0 (注意:力偶 M 的投影式和力矩式) 求:A处反力 解:整体(悬臂梁) x Ax F FAx F F q 3l cos 30 0 2 1 0 Fy FAy P F FAy 0 sin 30 0 A A M A M M q 3l l M F cos 30 3l F sin 30 l 0 2 1 0 (注:书中将分布载荷 q 变化为集中载荷画在图中不妥!) 例: θ 例: ? ? ? 例: FAx FAy FB
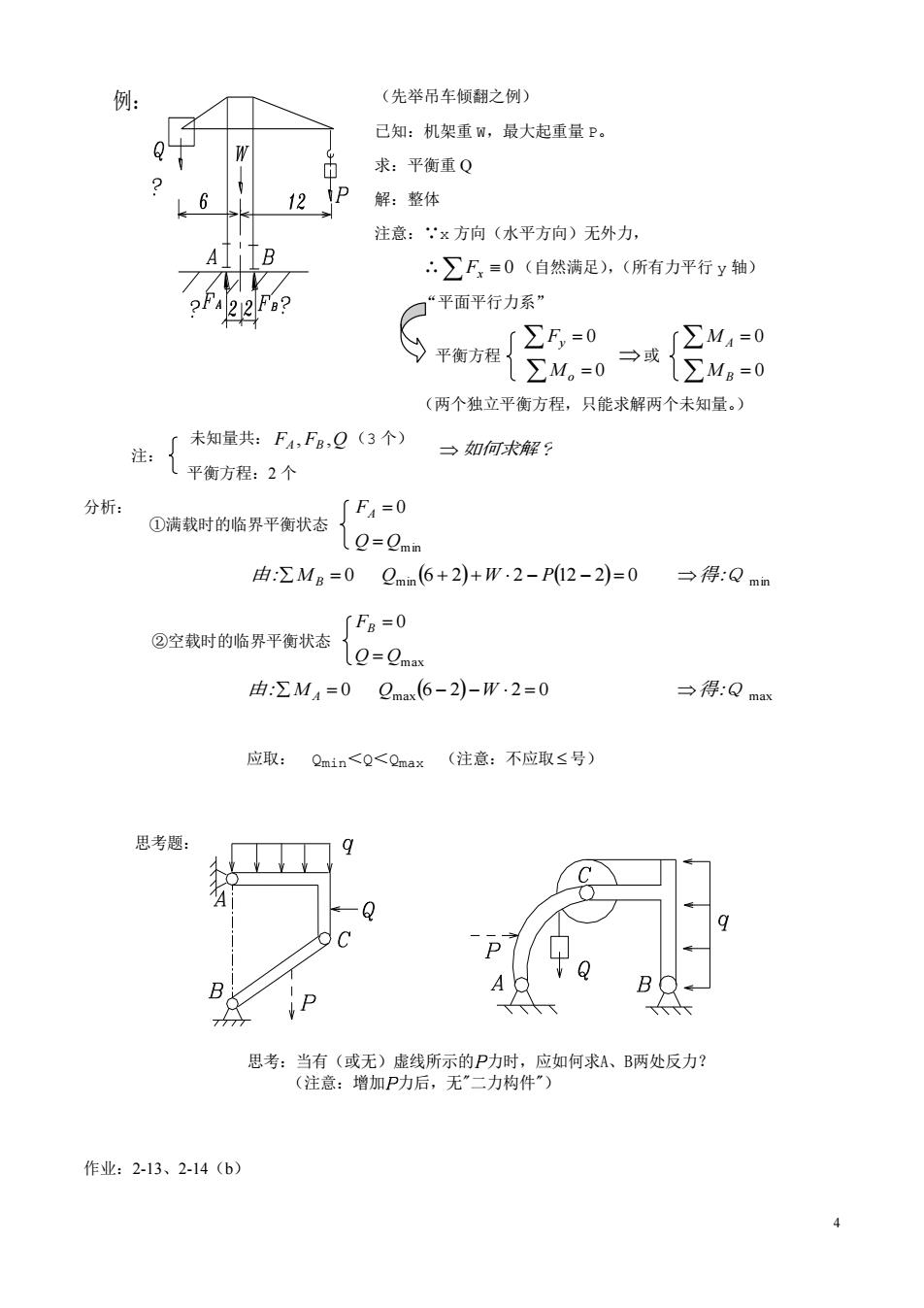
(先举吊车倾翻之例) 已知:机架重W,最大起重量P。 求:平衡重Q 12 解:整体 注意::x方向(水平方向)无外力, “∑F=0(自然满足),(所有力平行y轴) ☑“平面平行力系” 〔∑F,=0 9平有方程{乞以,0 ∑M4=0 1∑MB=0 (两个独立平衡方程,只能求解两个未知量。) 未知量共:F4,F,Q(3个) 三如向求解9 分析: 0满能时的临界平有状态{Q=0。 〔F4=0 由,:∑Mg=0Qmn(6+2)+W.2-P12-2)=0 →得:Qmn 「Fa=0 ②空载时的临界平衡状态1Q=Q 由:∑M4=0Qmax(6-2)-W.2=0 →得:Qmx 应取:Qin<Q<Qax(注意:不应取≤号) 思考题 9 应如何求A、B两处反力? 作业:2-13、2-14(b)
4 (先举吊车倾翻之例) 已知:机架重 W,最大起重量 P。 求:平衡重 Q 解:整体 注意:∵x 方向(水平方向)无外力, ∴ Fx 0 (自然满足),(所有力平行 y 轴) “平面平行力系” Fy 0 M A 0 Mo 0 M B 0 (两个独立平衡方程,只能求解两个未知量。) 未知量共: FA , FB ,Q (3 个) 平衡方程:2 个 分析: FA 0 Q Qmin 由: MB 0 Qmin 6 2 W 2 P12 2 0 得:Q min FB 0 Q Qmax 由: M A 0 Qmax6 2 W 2 0 得:Q max 应取: Qmin<Q<Qmax (注意:不应取 号) 作业:2-13、2-14(b) 例:思考题: 思考:当有(或无)虚线所示的 力时,应如何求A、B两处反力? (注意:增加 力后,无"二力构件") 平衡方程 或 注: 如何求解? ①满载时的临界平衡状态 ②空载时的临界平衡状态