实验三纯弯曲梁的正应力实验 一、实验目的: 1,用应变电测方法测定矩形截面梁纯弯曲段正应力的大小及正应力分布规律,将实验 值与理论值进行比较: 2.了解多点检测和自动检测技术在应变电测中的应用: 掌握电阻应变测量方法的原理和操作 二、实验设备: 1.材料力学综合试验台,主要由加载架、组合梁、力传感器等组成: 2.力、应变综合试验仪: 三、试样的准备: 1.贴有应变片的矩形截面梁(事先己贴好),如图3.1所示。 图3.1实验用矩形截面梁 四、实验原理及方法: 材料力学对平面弯曲正应力计算做过两个假设,1、平面假设:原为平面的梁横截面, 在变形后仍保持为平面。2、各纵向纤维之间互相没有挤压。在这些假设的基础上,得到梁 受纯弯曲时的正应力计算公式: (3.1) 式中:M一作用在横截面上的弯矩: y一欲求应力点到中性轴的距离: 【z一横截面对中性轴Z的惯性矩
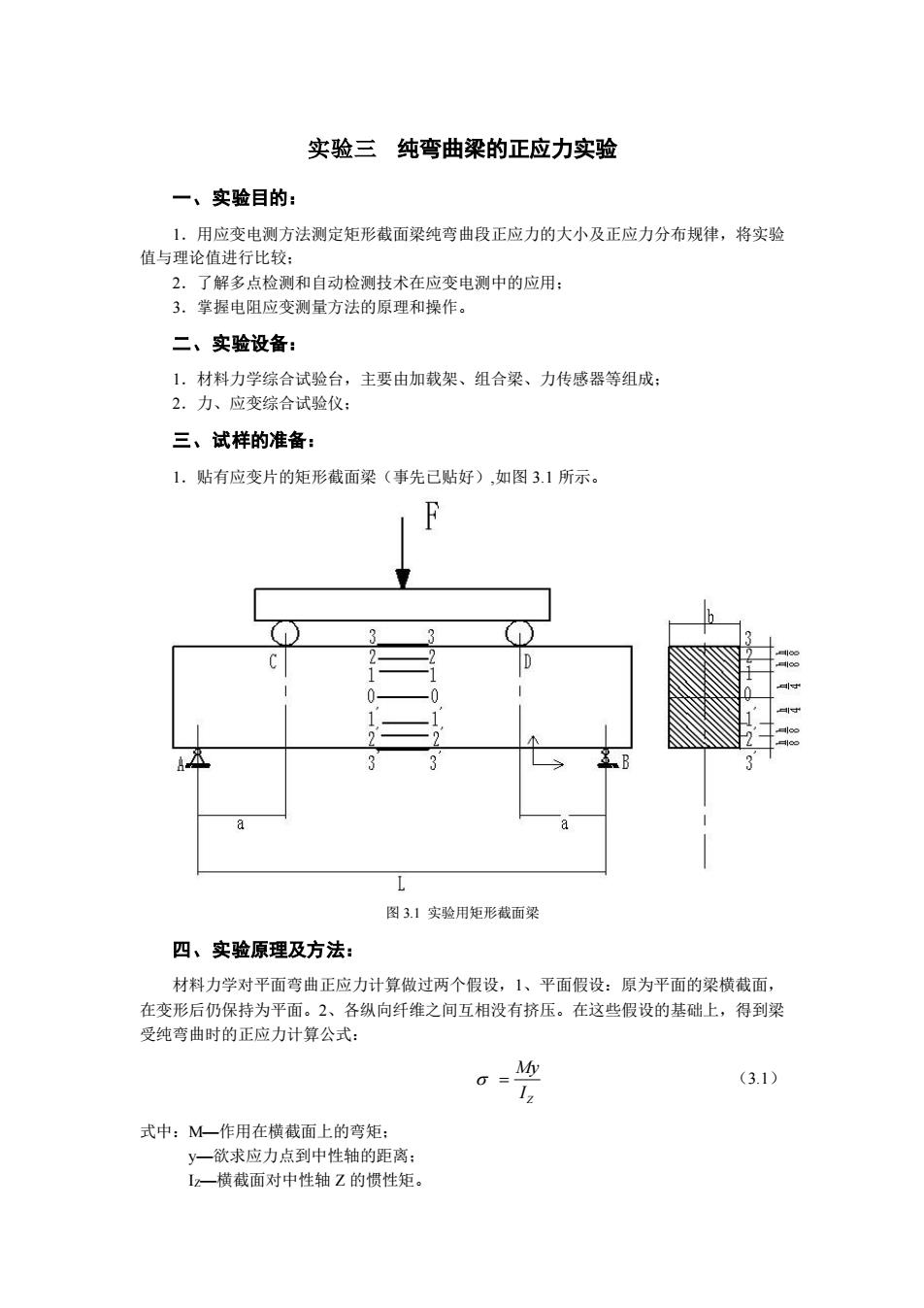
实验三 纯弯曲梁的正应力实验 一、实验目的: 1.用应变电测方法测定矩形截面梁纯弯曲段正应力的大小及正应力分布规律,将实验 值与理论值进行比较; 2.了解多点检测和自动检测技术在应变电测中的应用; 3.掌握电阻应变测量方法的原理和操作。 二、实验设备: 1.材料力学综合试验台,主要由加载架、组合梁、力传感器等组成; 2.力、应变综合试验仪; 三、试样的准备: 1.贴有应变片的矩形截面梁(事先已贴好),如图 3.1 所示。 图 3.1 实验用矩形截面梁 四、实验原理及方法: 材料力学对平面弯曲正应力计算做过两个假设,1、平面假设:原为平面的梁横截面, 在变形后仍保持为平面。2、各纵向纤维之间互相没有挤压。在这些假设的基础上,得到梁 受纯弯曲时的正应力计算公式: Z My I = (3.1) 式中:M—作用在横截面上的弯矩; y—欲求应力点到中性轴的距离; IZ—横截面对中性轴 Z 的惯性矩

FIID Fa LIID 图32纯弯曲矩形梁的剪力图、弯矩图 如图3.2所示分别为简支梁的受力图、剪力图和弯矩图。当C、D两处同时受F力作用 时,梁的CD段为纯弯曲段,弯矩为M=Fa,AC和DB部分为横力弯曲。实验时在梁的纯 弯曲段,沿梁的横截面不同高度刻画与沿轴线方向的平行线并贴上电阻应变片。原则是在梁 的中性层处贴一片,在中性轴两侧对称位置10mm、15mm、20mm(梁项端和底端)分别贴 三片,共贴有7片,称为工作片(见图3.1)。在一小块和梁相同的材料上贴上一枚与工作片 各项参数相同的应变片作为温度补偿片。实验时,采用温度补偿片法遂点测量7个点的纵向 应变,将每一待测工作片和温度补偿片按半桥接线方法一并接入应变仪,测出在载荷作用 下每个待测点的应变,温度补偿片要放在试验梁附近。由于纤维之间不互相挤压,故可根据 单向胡克定律求出实验应力σ,即: 0=E8零 (3.2) 式中:E为材料的弹性模量: 。实为实验应力计算值: £为实验应变测量值: 另外,由弯曲正应力公式。=少,又可以求出各点应力的理论值,于是可以将实测 值和理论值进行比较,计算出各点的误差,从而验证弯曲正应力公式的正确性。 实验采用增量法加载,每增加等量的载荷△F,测定各点相应的应变增量一次,载荷共 增加三次,依次得到三组应变值。重复三次,取三次应变增量的平均值△,依次求出各 点的实验的应力差值 G=E△E (3.3) 实验以Fo=30ON为初载荷,以Fma=180ON为最大载荷,采用等量分级加载法加载,载
图 3.2 纯弯曲矩形梁的剪力图、弯矩图 如图 3.2 所示分别为简支梁的受力图、剪力图和弯矩图。当 C、D 两处同时受 F 力作用 时,梁的 CD 段为纯弯曲段,弯矩为 M=Fa,AC 和 DB 部分为横力弯曲。实验时在梁的纯 弯曲段,沿梁的横截面不同高度刻画与沿轴线方向的平行线并贴上电阻应变片。原则是在梁 的中性层处贴一片,在中性轴两侧对称位置 10mm、15mm、20mm(梁顶端和底端)分别贴 三片,共贴有 7 片,称为工作片(见图 3.1)。在一小块和梁相同的材料上贴上一枚与工作片 各项参数相同的应变片作为温度补偿片。实验时,采用温度补偿片法逐点测量 7 个点的纵向 应变, 将每一待测工作片和温度补偿片按半桥接线方法一并接入应变仪,测出在载荷作用 下每个待测点的应变,温度补偿片要放在试验梁附近。由于纤维之间不互相挤压,故可根据 单向胡克定律求出实验应力 σ 实,即: σ 实=Eε 实 (3.2) 式中:E 为材料的弹性模量; σ 实为实验应力计算值; ε 实为实验应变测量值; 另外,由弯曲正应力公式 Z My I = ,又可以求出各点应力的理论值,于是可以将实测 值和理论值进行比较,计算出各点的误差,从而验证弯曲正应力公式的正确性。 实验采用增量法加载,每增加等量的载荷 ΔF,测定各点相应的应变增量一次,载荷共 增加三次,依次得到三组应变值。重复三次,取三次应变增量的平均值 Δε 实,依次求出各 点的实验的应力差值 σ 实。 σ 实=EΔε 实 (3.3) 实验以 F0=300N 为初载荷,以 Fmax=1800N 为最大载荷,采用等量分级加载法加载,载

荷增量为△F=50ON,观察各级应变增量是否等值。对于每一个测点,至少重复加载三次, 每次由Fo到Fm,测点i的应变为△s=(Ce0)。若三次的应变值很接近,将其同载荷下 同点的应变平均值作为该测点的应变。 A5 -AG+A6+A6] (3.4) 下标1、2、3表示第一、第二、第三次加载得到的应变增量 根据弯曲正应力理论,各测点的弯曲正应力理论值为: (3.5) 把以上理论值和实验值进行比较,以验证弯曲正应力公式。 计算各点的误差值: d=a-0选×100% (3.6) 0理 五、试验步骤: 1,试验前确定被测截面的尺寸、梁的长度、加力点位置与支座间的距离: 2.拟定实验方案: 3.根据初载荷和最大载荷值,以及其间至少应有3级加载的原则,确定每级载荷的大 小: 4.根据试样的布片情况和提供的设备条件确定最佳组桥方案并接线,根据桥路进行接 线,工作片接AB、补偿片接BC: 5.开机加载前,根据试验台传感器的负荷大小确定应变仪量程范围: 6.力、应变综合实验仪准备,力、应变综合实验仪标定(此项工作已提前完成): 7.打开仪器上面版,会看到接线部分的结构如图
荷增量为 ΔF=500N,观察各级应变增量是否等值。对于每一个测点,至少重复加载三次, 每次由 F0 到 Fmax,测点 i 的应变为 = (εin-εi0)。若三次的应变值很接近,将其同载荷下 同点的应变平均值作为该测点的应变。 1 2 3 1 3 i = + + (3.4) 下标 1、2、3 表示第一、第二、第三次加载得到的应变增量。 根据弯曲正应力理论,各测点的弯曲正应力理论值为: i z Fa y I 理论 = (3.5) 把以上理论值和实验值进行比较,以验证弯曲正应力公式。 计算各点的误差值: 100% i i i i − = 理 实 理 (3.6) 五、试验步骤: 1.试验前确定被测截面的尺寸、梁的长度、加力点位置与支座间的距离; 2.拟定实验方案; 3.根据初载荷和最大载荷值,以及其间至少应有 3 级加载的原则,确定每级载荷的大 小; 4.根据试样的布片情况和提供的设备条件确定最佳组桥方案并接线,根据桥路进行接 线,工作片接 AB、补偿片接 BC; 5.开机加载前,根据试验台传感器的负荷大小确定应变仪量程范围; 6.力、应变综合实验仪准备,力、应变综合实验仪标定(此项工作已提前完成); 7.打开仪器上面版,会看到接线部分的结构如图

CH1 CH2 CH12 桥路选择 0 D1 1/4 0 D3 CH CH2 CH12 桥路选择 0D D D3 半桥 CH1 CH2 CH12 桥路选择 A A n nn-- ☐001■ D2 003 全桥 D 8.根据要求接线,应变仪设有14桥、半桥、全桥三种测量方式 9.将各测点分别接入A、B、C、D端,B1为测量电桥的辅助接线端,以实现1/4桥测 试时的稳定测量,半桥、全桥测试时不使用B1端: 10。测量参数的设定,根据测试要求接好线后,首先打开电源,仪器预热20分钟后, 根据应变片灵敏系数进行设定,(具体在仪器中介绍): 11.仪器调整,载荷调整为以国际单位N显示,加初载荷Fo=30ON: 12.具体测试时一般采用手动测试状态进行,对各测点逐一进行单点平衡,反复三次平 衡后,施加载荷增量△F=50ON: 13.读取各点应变值,缓慢均匀地逐级加载,每增加一级载荷,记录各点应变片的读数 值: 14.将初始应变读数记录下来或将各测点单点平衡(反复调整为零),将机器调整为手 动挡: 15.载荷分三次加载,依次读取各点的应变值,实验重复三次: 16.试验结束由教师检查数据是否合格并签字: 7.试验结束,卸去载荷,关闭电源、拆线(注意拆线时动作要轻,以免叉子掉下来, 如果叉子已掉下,及时通知老师焊上): 六、实验数据处理: 1.每次加载由Fo到Fm,测点I的应变为(eo)如:Fo=300N,仪器应变的各测点 都调为零,F1=800N,此时记录各测点的应变读数,然后增加载荷F=1300N,再次记录
8.根据要求接线,应变仪设有 1/4 桥、半桥、全桥三种测量方式; 9.将各测点分别接入 A、B、C、D 端,B1 为测量电桥的辅助接线端,以实现 1/4 桥测 试时的稳定测量,半桥、全桥测试时不使用 B1 端; 10.测量参数的设定,根据测试要求接好线后,首先打开电源,仪器预热 20 分钟后, 根据应变片灵敏系数进行设定,(具体在仪器中介绍); 11.仪器调整,载荷调整为以国际单位 N 显示,加初载荷 F0=300N; 12.具体测试时一般采用手动测试状态进行,对各测点逐一进行单点平衡,反复三次平 衡后,施加载荷增量△F=500N; 13.读取各点应变值,缓慢均匀地逐级加载,每增加一级载荷,记录各点应变片的读数 值 εi; 14.将初始应变读数记录下来或将各测点单点平衡(反复调整为零),将机器调整为手 动挡; 15.载荷分三次加载,依次读取各点的应变值,实验重复三次; 16.试验结束由教师检查数据是否合格并签字; 17.试验结束,卸去载荷,关闭电源、拆线(注意拆线时动作要轻,以免叉子掉下来, 如果叉子已掉下,及时通知老师焊上); 六、实验数据处理: 1.每次加载由 F0 到 Fmax,测点 I 的应变为(εin-εi0)如:F0=300N,仪器应变的各测点 都调为零,F1=800 N,此时记录各测点的应变读数 εin,然后增加载荷 F2=1300 N,再次记录

各测点的应变读数cm,最后增加载荷F=1800N,然后再次记录各测点的应变读数n。此 时实验第一遍结束,共重复做三遍,取三遍各点的同载荷的平均值来计算各点的实验值。 2.在纯弯曲段,弯矩的增量为M=△F,由弯曲正应力计算公式计算各点的理论值为: 。 式1, 3.对每一个测点求出。对。的相对误差: 6=0理-0生x100% 0理 在梁的中性层,因。0,故只需计算绝对误差。 4.整理实验报告时,表3.1可供参考。 七、预习及思考题: 预习本节内容,并回答问题。 1.在梁的横力弯曲部分,弯曲正应力的计算仍用纯弯曲公式计算,与实验结果验证, 试问是否有很大误差? 2.整理实验数据时,对中间几个测点,应取前后两枚应变片应变的平均值。试问在实 测中这一平均值可用什么方法直接得到?
各测点的应变读数 εin,最后增加载荷 F3=1800 N,然后再次记录各测点的应变读数 εin。此 时实验第一遍结束,共重复做三遍,取三遍各点的同载荷的平均值来计算各点的实验值。 2.在纯弯曲段,弯矩的增量为 M=ΔFa,由弯曲正应力计算公式计算各点的理论值为: Z My I = 式中: 1 3 12 I bh = 。 3.对每一个测点求出 σ 实对 σ 理的相对误差: 100% − = 理 实 理 在梁的中性层,因 σ 理=0,故只需计算绝对误差。 4.整理实验报告时,表 3.1 可供参考。 七、预习及思考题: 预习本节内容,并回答问题。 1.在梁的横力弯曲部分,弯曲正应力的计算仍用纯弯曲公式计算,与实验结果验证, 试问是否有很大误差? 2.整理实验数据时,对中间几个测点,应取前后两枚应变片应变的平均值。试问在实 测中这一平均值可用什么方法直接得到?
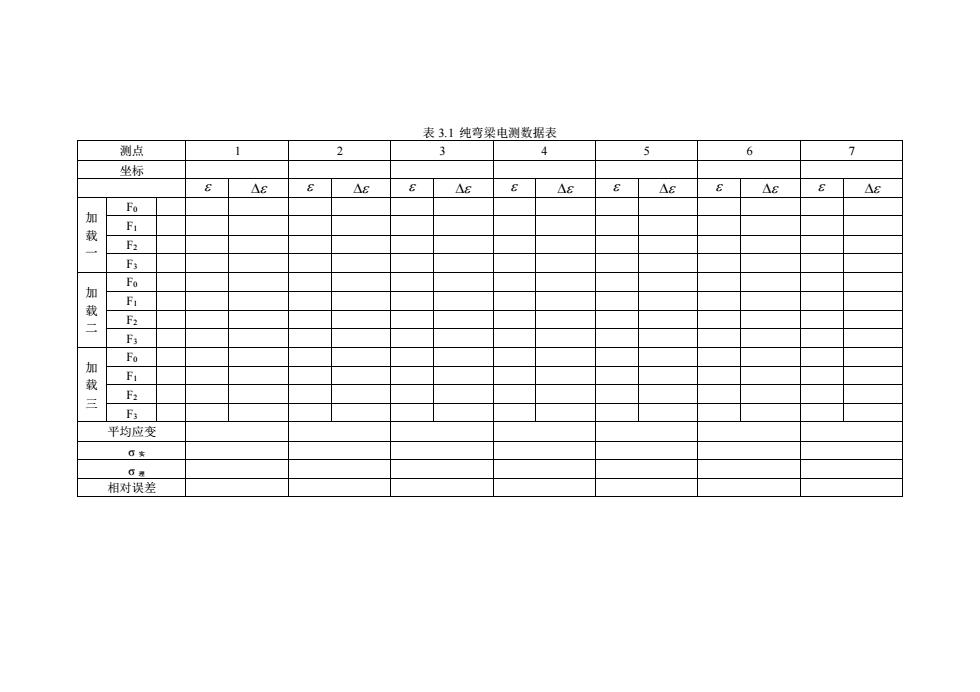
表31纯弯梁电测数据表 测点 1 2 5 6 7 坐标 △8 B△ Fo E, F. 平均应变 相对误差
表 3.1 纯弯梁电测数据表 测点 1 2 3 4 5 6 7 坐标 加载一 F 0 F 1 F 2 F 3 加载二 F 0 F 1 F 2 F 3 加载三 F 0 F 1 F 2 F 3 平均应变 σ 实 σ 理 相对误差