北京化工大学：《理论力学》课程教学资源（教案讲义）第五章 点的运动学 第六章 刚体的简单运动

(10) 运动学 (仅从几何观点研究物体的运动。即：仅研究物体运动的几何性质而不考虑引起其变化的原因) 点的运动学 运动轨迹 内容 刚体运动学 运动轨律 运动方程 位移、速度和加速度， 运动描述→参考体→参考系（一般工程问题中，取固连于地球上的参考系：静（定）坐标系) 第五章点的运动学（介绍要点，自学复习） 「1、点的运动方程 「1、矢量法（矢径法） 主要内容 (2、点的速度、加速度 基本方法了2、直角坐标法 (3、自然法（弧坐标法） §5-1矢量法（矢径法，主要用于理论推导》 运动方程：下=)，矢端曲线即为动点轨迹 AM 速度：下 d而 (下=产) →方向沿轨迹切线方向 0(定点) dr 加速度：ā=da 布d2行 (a=市=前 S5-2直角坐标法 人 有：F=x++k [x=f0 = ax=x=求 、三之至丝运动1少=0 速度（投影y,=少 加速度（投影）ay=y=立 =2 a.=.= 红 (又：消去时间1可得点的轨迹方程) 由投影可得下、ā的大小和方向 §5-3自然法（弧坐标法）（用于动点运动轨迹己知的情况（且特别是在轨迹为圆弧的情况时更为简便） 0.M中轨迹 运动方程：S=f)“代数量” ds ,方向：沿轨迹切线方向 速度：V () dt 「>0：沿轨迹正向 1代数量：1<0：沿轨迹负向 可表苏浙=帝仁词 (T:沿轨迹切线正向的单位矢量)

1 (v r) dt dr v    (v r) dt dr v   ( ) 2 2 a v r dt d r dt dv a               ( ) ( ) ( ) 3 2 1 z f t y f t x f t         ( ) ( ) ( ) 3 2 1 z f t y f t x f t         v z v y v x z y x            ( ) ( ) ( ) 3 2 1 z f t y f t x f t            a v z a v y a v x z z y y x x               ( ) ( ) ( ) 3 2 1 z f t y f t x f t 运动学 （仅从几何观点研究物体的运动。即：仅研究物体运动的几何性质而不考虑引起其变化的原因） 点的运动学 运动轨迹 刚体运动学 运动轨律 运动方程 位移、速度和加速度， 运动描述  参考体  参考系(一般工程问题中，取固连于地球上的参考系：静(定)坐标系) 第五章 点的运动学（介绍要点，自学复习） 1、点的运动方程 1、矢量法（矢径法） 2、点的速度、加速度 基本方法 2、直角坐标法 3、自然法（弧坐标法） §5-1 矢量法（矢径法，主要用于理论推导） 运动方程： r  rt ，矢端曲线即为动点轨迹。 速度：  方向沿轨迹切线方向 加速度： §5-2 直角坐标法 有： r  xi  yj  zk 运动方程 速度(投影) 加速度(投影) (又：消去时间 t 可得点的轨迹方程) §5-3 自然法（弧坐标法）（用于动点运动轨迹已知的情况（且特别是在轨迹为圆弧的情况时更为简便） 运动方程： S  f (t) “代数量” 速度： 可表示为：   ( s ) dt ds v  v    (  ：沿轨迹切线正向的单位矢量) (定点) (-) (＋) 轨迹 内容 主要内容 （10） 由投影可得 v、 a 的大小和方向 (s) dt ds v   方向：沿轨迹切线方向 代数量： ＞0：沿轨迹正向 ＜0：沿轨迹负向

加速度：☆切向加速度：a==5 代数量>0：沿轨迹正向 <0:沿轨迹负向 (反应速度大小变化率) 也可表示为：a,=a,f=7=57 ☆法向加速度：0，一二厂方向：恒指向曲事中心 pL恒为正值 (反映速度方向变化率) 也可表示为：豆厅一弓n万：主法线方向的单位矢量) 个石（副法线） a 注了☆全加速度石在由切线和主法线组成的密切面内 主法线 0 气（切线） an L☆全加速度ā在副法线上的分量为零（副法线：垂直密切面的法线） “自然轴 「①利用直角坐标法和自然法写出点的运动方程。 要求 【②利用运动方程及有关公式求出点的速度和加速度 (注：§64柱坐标、极坐标不要求) 第六章刚体的简单运动平行移动平移 1定轴转动（转动） (基本运动 (注：1、工程中应用广泛：2、研究复杂运动的基础 §6-1刚体的平行移动 A 例：“振动式送料机”：运动中、始终有：AB1∥AB “平移”（平动）：运动中，刚体内任意一直线始终与原位置平行。 〔点B:TB=rg() 由矢量法 (点A:下4=(0=g+BA 点B:可=di 速度 点A岳品，+岳=，函：常关副 d 同理：加速度有：a4=ag 结含：平移（公件务客费糖网加生度阳明→平移利愿可自结为点的运动学运 例： 已知：p=0): 击：平移{直级干营（保 求：人手点M的速度、加速度

2 (+) φ 例: n v an an n  2   方向：恒指向曲率中心  恒为正值 2 v an  点 A： B B B A A v dt dr r BA dt d dt dr v   (  )   n t t n a a tg a n a a a    ( , ) 2 2  大小： 方向： 加速度：☆切向加速度： a v s t     代数量 (反应速度大小变化率) 也可表示为： a a  v s t t      ☆法向加速度： (反映速度方向变化率) 也可表示为： n： 主法线方向的单位矢量）  (全)加速度： a  at  an  at   ann  ☆.全加速度 a 在由切线和主法线组成的密切面内 ☆.全加速度 a 在副法线上的分量为零（副法线：垂直密切面的法线） ①利用直角坐标法和自然法写出点的运动方程。 ②利用运动方程及有关公式求出点的速度和加速度 （注：§6-4 柱坐标、极坐标不要求） 第六章 刚体的简单运动 (基本运动) (注：1、工程中应用广泛；2、研究复杂运动的基础) §6-1 刚体的平行移动 例：“振动式送料机”；运动中、始终有：A1B1∥AB “平移”(平动)：运动中，刚体内任意一直线始终与原位置平行。 由矢量法 速度 同理：加速度有： aA  aB 结论：平移  平移问题可归结为点的运动学问题 已知：  (t) ； 注：平移 （举例） 求：人手点 M 的速度、加速度。 θ 注 ( BA ：常矢量) ＞0：沿轨迹正向 ＜0：沿轨迹负向 要求 τ（切线） "自然轴" （主法线） （副法线） 平行移动(平移) 定轴转动(转动) 点 B： r r (t) B  B 点 A：rA  rA (t)  rB  BA 点 B： dt dr v B B  1、刚体上各点轨迹相同 2、每一瞬时各点速度、加速度相同 直线平移 曲线平移

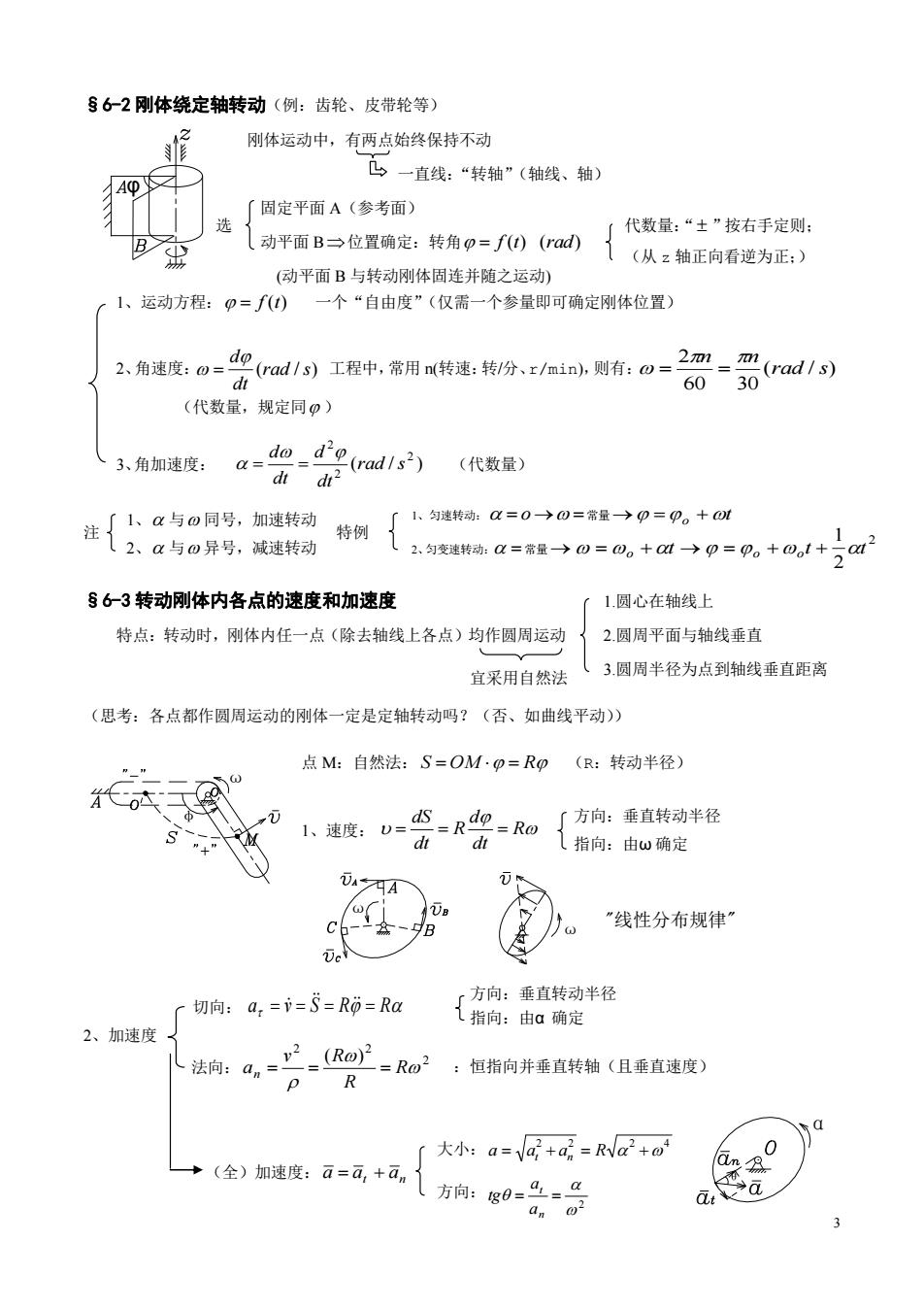
S62刚体绕定轴转动（例：齿轮、皮带轮等） 刚体运动中，有两点始终保持不动 山一直线：“转轴”（轴线、轴 「固定平面A(参考面) 选 代数量：“±”按右手定则： B 动平面B→位置确定：转角p=f0v）1(从2轴正向看逆为正：) (动平面B与转动刚体固连并随之运动) 1、运动方程：O=f()一个“自由度”（仅需一个参量即可确定刚体位置） 2、角速度：0= do d1)T脚，常用钱迷制分ain周有：a=2测-ad/ (代数量，规定同0) 3角加速度：a--(ad1s dt dr2 (代数量) 公a0 特例陆a=0→0=量→p=,十 §63转动刚体内各点的速度和加速度 1圆心在轴线上 特点：转动时，刚体内任一点（除去轴线上各点）均作圆周运动 2.圆周平面与轴线垂直 宜采用自然法 、3.圆周半径为点到轴线垂直距离 (思考：各点都作圆周运动的刚体一定是定轴转动吗？（否、如曲线平动）) 点M:自然法：S=OM·=Rp(R:转动半径) 1速度：U-少=R吧=R 了方向：垂直转动半径 d (指向：由ω确定 A ( ck “线性分布规律 e 切向：a,=i=5=R0=Ra 方向：垂直转动半径 2、加速度 指向：由a确定 法向：4，一二_R。R0:恒指向并垂直转轴（且垂直速度） p R 大小：a=V同+a7=Rva2+o (全)加速度：a=a,+an 方向：g0==只 d o2

3 （代数量，规定同  ） ( / ) 2 2 2 rad s dt d dt d     1、 与  同号，加速转动 2、 与  异号，减速转动 §6-2 刚体绕定轴转动（例：齿轮、皮带轮等） 刚体运动中，有两点始终保持不动 一直线：“转轴”（轴线、轴） 固定平面 A（参考面） 动平面 B  位置确定：转角   f (t) (rad) (动平面 B 与转动刚体固连并随之运动) 1、运动方程：   f (t) 一个“自由度”（仅需一个参量即可确定刚体位置） 2、角速度： (rad / s) dt d   工程中，常用 n(转速：转/分、r/min)，则有： ( / ) 60 30 2 rad s n n    3、角加速度： （代数量） 注 特例 §6-3 转动刚体内各点的速度和加速度 1.圆心在轴线上 特点：转动时，刚体内任一点（除去轴线上各点）均作圆周运动 2.圆周平面与轴线垂直 3.圆周半径为点到轴线垂直距离 （思考：各点都作圆周运动的刚体一定是定轴转动吗？（否、如曲线平动）） 点 M：自然法： S  OM   R （R：转动半径） 1、速度： 2、加速度 （全）加速度： a  at  an φ 方向：垂直转动半径 指向：由ω 确定 φ ω ω ω "线性分布规律"θ α 选 代数量：“  ”按右手定则； （从 z 轴正向看逆为正；） 1、匀速转动：   o   常量 t  o  2、匀变速转动：   常量 2 2 1 t t t   o    o o   宜采用自然法    R dt d R dt dS    方向：垂直转动半径 指向：由α 确定 ：恒指向并垂直转轴（且垂直速度） 切向： a  v   S   R   R 法向： 2 2 2 ( )    R R v R an    大小： 2 2 2 4 a  at  an  R   方向： 2      n t a a tg

,1每一解时，各点速度、加速度的大小与转动半径成正比即：线性分布规律 特点 2每一解时，各点（全）加速度与转动半径间的夹角均相等一即：日与点位置无关 a 思考：①分析轮上A、B两点 A ②纸筒的纸速度为常量， 与绳上A、B两点的速度和加速度 ☐lza 求：纸筒的角加速度。 §64轮系的传动此（定轴轮系的传动计算） 1、齿轮传动： 外啮合 内啮合 有：0R=0,R→9=B=立 (注意：外、内啮合的区别点：即0、2的转向关系) 传动此：--尽= 2R 01 02 2、皮带轮传动 (也有转向不相同的情况) (与齿轮传动相比，皮带轮传动易“丢转”，但不易超载引起破坏) (传动比1：表示变速传动的程度11：诚速传动。) (二级变速)减速箱 n 解 已知：1一24及m1:求：n4 =%=4 n 有：m2=n n2 nana 13 注：轮系的总传动比等于各级传动比的连乘积（分子为各从动轮齿数，分母为各主动轮齿数） §65以矢量表示角速度及角加速度，以矢积表示点的速度和加速度 12 a=0k 按右手定则 a=ak 速度：下=而×F 加速度：a dv d a. 作业：6-3、64 4

4 即： 1 3 2 4 14 4 1 4 3 2 1 12 34 z z z z i n n n n n n i i         有： n2  n3 α ω α ω 按右手定则       k k     1.每一瞬时，各点速度、加速度的大小与转动半径成正比 即：线性分布规律 特点 2.每一瞬时，各点（全）加速度与转动半径间的夹角θ 均相等 即：θ 与点位置无关 思考：①分析轮上 A、B 两点 与绳上 A、B 两点的速度和加速度 §6-4 轮系的传动比（定轴轮系的传动计算） 1、齿轮传动： （注意：外、内啮合的区别点：即 1 、2 的转向关系） 传动比： (也可取： ) 2、皮带轮传动 （也有转向不相同的情况） （与齿轮传动相比，皮带轮传动易“丢转”，但不易超载引起破坏） （传动比 i ：表示变速传动的程度 i＜1 ：增速传动； i＞1 ：减速传动。） （二级变速）减速箱 已知： 1 z ～ 4 z 及 1 n ；求： 4 n §6-5 以矢量表示角速度及角加速度，以矢积表示点的速度和加速度 速度： v  r 作业：6-3、6-4 ω α θ θ ω ω 外啮合 ω ω 内啮合 ω ω 例： ②纸筒的纸速度为常量， 求：纸筒的角加速度。 有： 1 2 1 2 2 1 1 1 2 2 z z R R R  R        1 2 1 2 2 1 12 z z R R i      1 2 1 2 2 1 12 z z R R i        “＋”：内啮合 “—”：外啮合 1 2 2 1 12 r r i     1 2 2 1 12 z z n n i   1 2 2 1 12 z z n n i   3 4 4 3 34 z z n n i   1 2 2 1 12 z z n n i   解 注：轮系的总传动比等于各级传动比的连乘积（分子为各从动轮齿数，分母为各主动轮齿数）   at an r v dt dr r dt d r dt d dt dv a             加速度： ( )