
(1) 绪论 「理论力学(研究物体机械运动的一般规律)。 工程力学(基础) (材料力学(研究构件的承载能刀〉 (机械专业主干基础课) 了机械运可:物体在空间的位置随时间的变化 (宏观物体远小于光速的运动,“古典力骨”范畴,以伽利略、牛顿(17.18世纪)建立的理论为基础。) 「相对论 承载能刀:①强度②刚度③稳定性 香则量子学(微现》 ①静力学(研究力系的平衡问题) 理论力学 ②运动学(仅从几何观点来研究运动,也即:不考虑引起运动变化的原因) ③动力学(研究物体运动变化和作用力的关系) 「★直接应用 最密切 ★间接应用(后续课:机原、材力、机零(机设),弹性力学、有限元…等。) 力学教有·素质教有(范) 一士兵过桥 介绍实例:①吊车倾翻 ②振动了 球迷踏脚 汽车频率 水果摘取“2116”工程 ③折叠式潜艇 (又:定向爆破时,烟筒倒下时从何处断?) 阳台 ⑤手榴弹(反强度问题,与容器相反) ©稳定(社科院脚手架) ⑦断裂问题(美国飞机失事) 〔①概念:“准确” 掌握基本概念,主要公式及定理 学习要求 ②方法:“简明” 明确解题方法及步骤。 ③训练:“独立” 作好基本训练,独立完成作业 静力学研面国图图{中钢施物上价运动 机械运动的一种特殊形式。 1、物体的受力分析。 主要内容 2、力系的等效替换(及简化)。 3、各种力系的平衡条件
1 士兵过桥 球迷踏脚 汽车频率 水果摘取“2116”工程 相对论 量子力学(微观) 力系:作用在物体上的一群力。 平衡:相对地球静止,或匀速直线运动。 绪论 理论力学 (研究物体机械运动的一般规律)。 材料力学 (研究构件的承载能力) 机械运动:物体在空间的位置随时间的变化 (宏观物体远小于光速的运动,“古典力学”范畴,以伽利略、牛顿(17.18 世纪)建立的理论为基础。) 否则 承载能力:①强度 ②刚度 ③稳定性, ①静力学(研究力系的平衡问题) 理论力学 ②运动学(仅从几何观点来研究运动,也即:不考虑引起运动变化的原因) ③动力学(研究物体运动变化和作用力的关系) ★直接应用 最密切 ★间接应用(后续课:机原、材力、机零(机设),弹性力学、有限元…..等。) 力学教育 素质教育(范) 介绍实例: ①吊车倾翻 ②振动 ③折叠式潜艇 (又:定向爆破时,烟筒倒下时从何处断?) ④刚度 ⑤手榴弹(反强度问题,与容器相反) ⑥稳定(社科院脚手架) ⑦断裂问题(美国飞机失事) ①概念: “准确” 掌握基本概念,主要公式及定理 学习要求 ②方法: “简明” 明确解题方法及步骤。 ③训练: “独立” 作好基本训练,独立完成作业 静力学:研究力系的平衡问题 机械运动的一种特殊形式。 1、物体的受力分析。 主要内容 2、力系的等效替换(及简化)。 3、各种力系的平衡条件。 工程力学(基础) (机械专业主干基础课) 阳台 吊车 跳板 (1)

★基本概念 1、刚体:力作用下形状和大小保持不变的物体 →“理想模型”·“刚体静力学” (或:力作用下物体内任意两点距离保持不变) 体感支形 固体 (“刚体静力学” 一“变形体力学的基础) (流体」 「接触作用:面力等 了集中力 2、力:物体间的相互机械作用 场的作用:体力(引)等 又分布力 推数生 C大小 模(大小) 力的三要素了方向 “矢量”(向量、张量) F=FF0(国际单位制) C作用固 Fo 单位向量 第一章静力学公理和物体的受力分析 §1-1静力学公理 F=F+F2 公理1、力的平行四边形法则 “矢量和(几何和 (最简单的力系简化法则) 进而可得”力三角形法” 公理2、二力平衡条件 B 下=-万简:“等值、反向、共线” (最简单的力系平衡条件) ①注意万=-F与E1=2的区别与联系 ②此公理对刚体为充、要条件,对变形体仅为必要条件。 公理3、加减平衡力系原理(在已知力系上加上或减去一任意平衡力系,不改变原力系对刚体的作用) 注:对刚体成立!对变形体需注意应用范围。(平衡力系对刚体的效应为零) 推理1、力的可传性原理(作用在刚体上某点的力,可以沿着力的作用线移到刚体内任一点) 「大小 ①对刚体力为滑动矢量了方向 加 作用国 ②适用于刚体,不适用于变形体 ③力沿作用线滑移,而非平移。 有:==-2 ④在同一刚体内滑移
2 ★基本概念 1、刚体:力作用下形状和大小保持不变的物体 “理想模型” “刚体静力学” (或:力作用下物体内任意两点距离保持不变) 固体 流体 接触作用: 面力等 集中力 场的作用: 体力(引力)等 分布力 运动效应(外效应):物体运动状态发生改变(“理力”内容) 变形效应(内效应):物体产生变形(“变形体力学”(材力)内容) 大小 F 模(大小) 力的三要素 方向 “矢量”(向量、张量) 0 F F·F (国际单位制) 作用点 0 F 单位向量 第一章 静力学公理和物体的受力分析 §1-1 静力学公理 公理 1、力的平行四边形法则 “矢量和”(几何和) (最简单的力系简化法则) 进而可得”力三角形法” 公 理 2 、 二 力 平 衡 条 件 F1 F2 简:“等值、反向、共线” (最简单的力系平衡条件) ①注意 F1 F2 与 F1=F2 的区别与联系 ②此公理对刚体为充、要条件,对变形体仅为必要条件。 公理 3、加减平衡力系原理 (在已知力系上加上或减去一任意平衡力系,不改变原力系对刚体的作用) 注:对刚体成立!!对变形体需注意应用范围。(平衡力系对刚体的效应为零) 推理 1、力的可传性原理(作用在刚体上某点的力,可以沿着力的作用线移到刚体内任一点) 大小 ①对刚体力为滑动矢量 方向 作用线 ②适用于刚体,不适用于变形体。 ③力沿作用线滑移,而非平移。 ④在同一刚体内滑移。 2、力: 物体间的相互机械作用 相对 “刚体” “变形体” (“刚体静力学” “变形体力学”的基础) 又 力的效应 有: 加 减
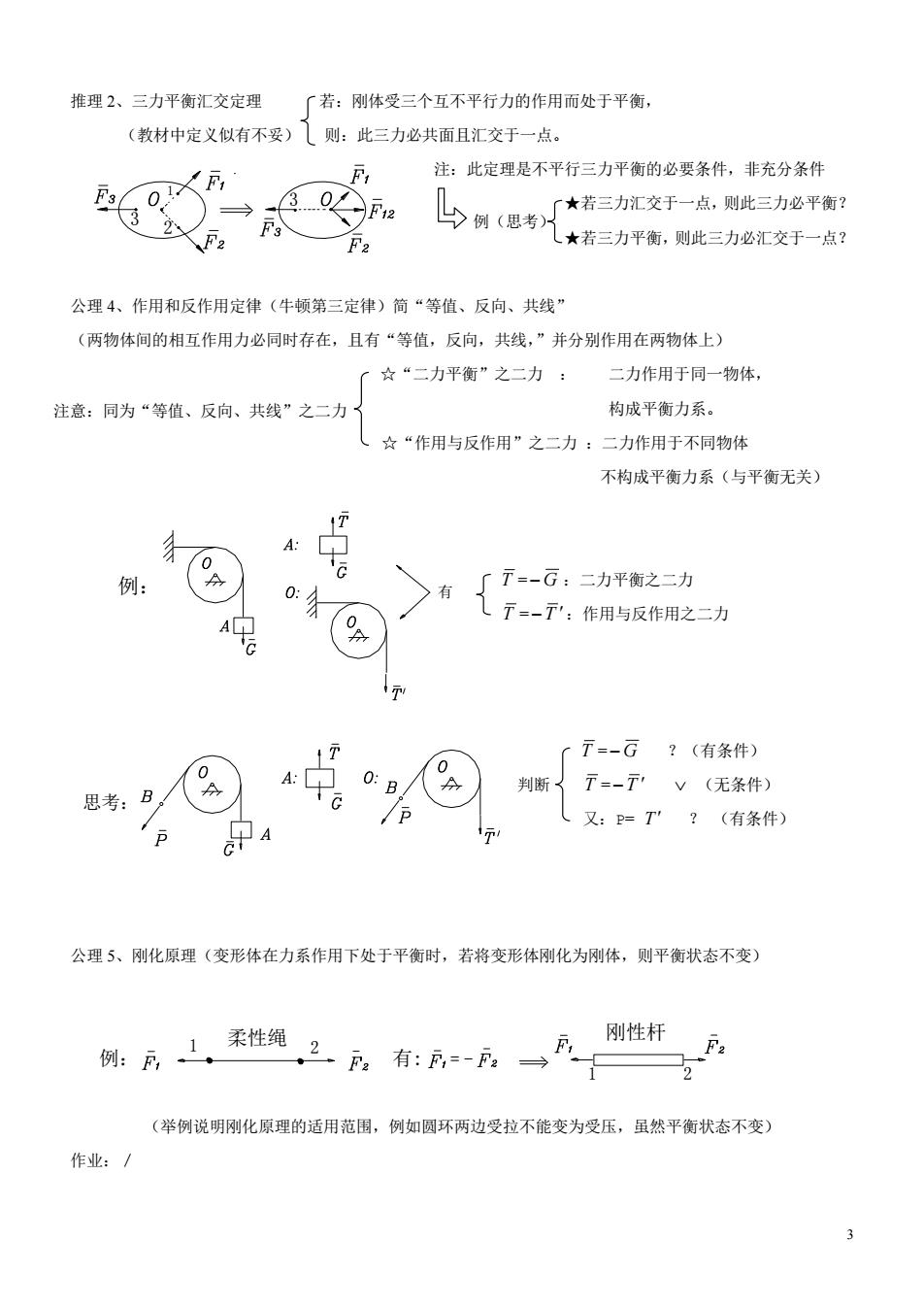
推理2、三力平衡汇交定理「若:刚体受三个互不平行力的作用而处于平衡, (教材中定义似有不妥)则:此三力必共面且汇交于一点。 注:此定理是不平行三力平衡的必要条件,非充分条件 马例思考大着三方交于一点则此三力公平衡? 2 F2 (★若三力平衡,则此三力必汇交于一点? 公理4、作用和反作用定律(牛顿第三定律)简“等值、反向、共线” (两物体间的相互作用力必同时存在,且有“等值,反向,共线,”并分别作用在两物体上) 「☆“二力平衡”之二力: 二力作用于同一物体 注意:同为“等值、反向、共线”之二力 构成平衡力系。 ,☆“作用与反作用”之二力:二力作用于不同物体 不构成平衡力系(与平衡无关) 例: 0: >有 「下=-G:二力平衡之二力 (下=一下':作用与反作用之二力 「T=-G?(有条件》 A: 0:B/ 0 V(无条件) 思考: 又:卫=T?(有条件) 1元/ 公理5、刚化原理(变形体在力系作用下处于平衡时,若将变形体刚化为刚体,则平衡状态不变) 例:, 刚性杆F (举例说明刚化原理的适用范围,例如圆环两边受拉不能变为受压,虽然平衡状态不变) 作业:/
3 推理 2、三力平衡汇交定理 若:刚体受三个互不平行力的作用而处于平衡, (教材中定义似有不妥) 则:此三力必共面且汇交于一点。 注:此定理是不平行三力平衡的必要条件,非充分条件 ★若三力汇交于一点,则此三力必平衡? ★若三力平衡,则此三力必汇交于一点? 公理 4、作用和反作用定律(牛顿第三定律)简“等值、反向、共线” (两物体间的相互作用力必同时存在,且有“等值,反向,共线,”并分别作用在两物体上) ☆“二力平衡”之二力 : 二力作用于同一物体, 构成平衡力系。 ☆“作用与反作用”之二力 :二力作用于不同物体 不构成平衡力系(与平衡无关) T = G :二力平衡之二力 T = T :作用与反作用之二力 T = G ?(有条件) 判断 T = T (无条件) 又:P= T ? (有条件) 公理 5、刚化原理(变形体在力系作用下处于平衡时,若将变形体刚化为刚体,则平衡状态不变) (举例说明刚化原理的适用范围,例如圆环两边受拉不能变为受压,虽然平衡状态不变) 作业:/ 例(思考) 注意:同为“等值、反向、共线”之二力 1 2 3 3 例: 有 思考: 例: 1 柔性绳 2 = - 刚性杆 1 2 有: